Проверка совпадения опытных и теоретических законов распределения ПН по критериям согласия
Теоретический закон распределения для выравнивания опытной информации выбирают: - в соответствие с областью применения ТЗР; - на основе визуального совпадения полигона опытного распределения с кривой дифференциальной функции ЗНР и ЗРВ; - по лучшему совпадению опытных точек информации с интегральной прямой ЗНР и ЗРВ; - по величине коэффициента вариации. Однако в некоторых случаях перечисленные методы выбора ТЗР могут не дать желаемого результата. В таких случаях ТЗР выбирают по критериям согласия. В теории вероятности применяют несколько критериев согласия. Применительно к ПН тракторов и сельскохозяйственных машин чаще всего используют критерий согласия Пирсона. Критерий согласия Пирсона
где
где Если исходная информация о показателе надежности представлена в виде статистического ряда, то определения критерия согласия Если нет статистического ряда, можно всю исходную информацию разбить на ряд интервалов разной величины по возрастающему значению ПН, чтобы В расчете доремонтных ресурсов двигателей укрупненный статистический ряд информации приведены в таблице 5.
Таблица 5. Укрупненный статистический ряд информации о доремонтных ресурсах двигателей
В случае ЗНР теоретическую частоту подсчитывают по уравнению (19) и по данным таблицы 1 Приложения. Для конца первого интервала укрупненного статистического ряда
Для конца второго интервала
В случае ЗРВ интегральную функцию определяют по таблице 9 приложения, вход в которую осуществляется по величине параметра Для конца первого интервала укрупненного статистического ряда
Теоретическую частоту до конца первого интервала определяют по уравнению (19):
Для второго интервала
ТЗР выбирают по величине критерия Для ЗНР:
для ЗРВ:
Судя по значениям критериев согласия
где Для ЗРВ, так же как и для ЗНР, число обязательных связей равно трем: две связи – два параметра распределения и третья связь Таким образом, в нашем расчете
Следовательно, значения критерия Следует иметь в виду, что критической вероятностью совпадения принято считать Рассчитав значения для ЗНР для ЗРВ Данные этого расчета согласуются с методом определения критерия согласия
|

 представляет собой сумму квадратов отклонений опытных и теоретических частот в каждом интервале статистического ряда информации:
представляет собой сумму квадратов отклонений опытных и теоретических частот в каждом интервале статистического ряда информации: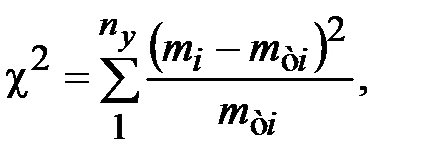 (18)
(18) - число интервалов в укрупненном статистическом ряду;
- число интервалов в укрупненном статистическом ряду;  - опытная частота в
- опытная частота в  интервале статистического ряда;
интервале статистического ряда; 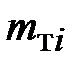 - теоретическая частота в
- теоретическая частота в 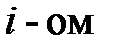 интервале;
интервале; (19)
(19) - количество точек информации;
- количество точек информации;  и
и  - интегральные функции соответственно в конце и начале
- интегральные функции соответственно в конце и начале  интервала значений показателей надежности.
интервала значений показателей надежности.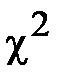 составляют укрупненный статистический ряд, соблюдая правило:
составляют укрупненный статистический ряд, соблюдая правило: 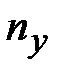
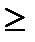 4,
4, 
 <5.
<5.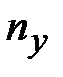
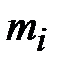
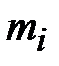
 по ЗНР
по ЗНР
 по ЗРВ
по ЗРВ

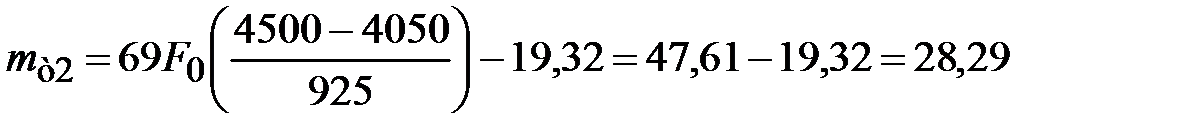 и т.д.
и т.д.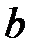 (
(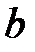 =3,34) и отношению
=3,34) и отношению  (
(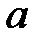 = 3083 мото-ч;
= 3083 мото-ч; 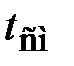 =1250 мото-ч).
=1250 мото-ч).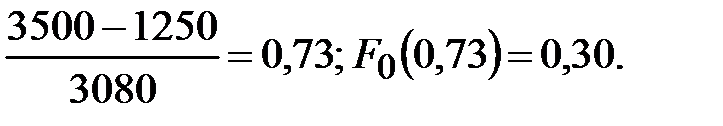
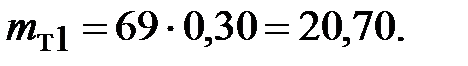
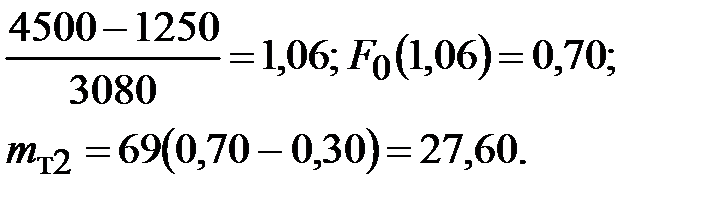
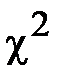 , который будет равен (уравнение 18) по данным таблицы 5:
, который будет равен (уравнение 18) по данным таблицы 5:
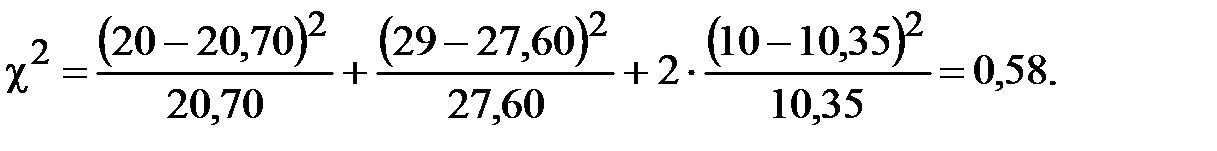
 , по таблице 6 Приложения определяют вероятность совпадения опытных и теоретических данных. Вероятность совпадения при прочих равных условиях зависит и от повторности использованной информации. Поэтому для входа в таблицу приложения необходимо определить число степеней свободы
, по таблице 6 Приложения определяют вероятность совпадения опытных и теоретических данных. Вероятность совпадения при прочих равных условиях зависит и от повторности использованной информации. Поэтому для входа в таблицу приложения необходимо определить число степеней свободы 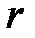 по уравнению:
по уравнению: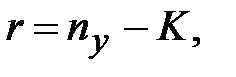 (20)
(20)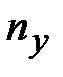 - число интервалов укрупненного статистического ряда;
- число интервалов укрупненного статистического ряда; 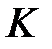 - число обязательных связей;
- число обязательных связей; 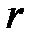 - число степеней свободы или номер строки в таблице 6 приложения.
- число степеней свободы или номер строки в таблице 6 приложения.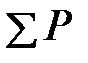 =1,0.
=1,0.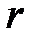 = 4 - 3= 1.
= 4 - 3= 1.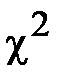 находим в первой строке, а вероятность совпадения определяем в заглавной строке (значение
находим в первой строке, а вероятность совпадения определяем в заглавной строке (значение 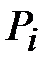 ) таблицы 6 Приложения. Таким образом, вероятность совпадения ЗНР (
) таблицы 6 Приложения. Таким образом, вероятность совпадения ЗНР (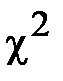 =0,15) составляет около 70%, а вероятность совпадения ЗРВ (
=0,15) составляет около 70%, а вероятность совпадения ЗРВ (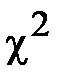 =0,58)-около 45%.
=0,58)-около 45%. < 10 %, выбранный для выравнивания теоретический закон распределения следует считать непригодным.
< 10 %, выбранный для выравнивания теоретический закон распределения следует считать непригодным. по уравнению (18), определив номер строки (число степеней свободы) по уравнению (19) и вероятность совпадения теоретических распределений с опытными по таблице 6 Приложения, окончательно получим:
по уравнению (18), определив номер строки (число степеней свободы) по уравнению (19) и вероятность совпадения теоретических распределений с опытными по таблице 6 Приложения, окончательно получим: =1,92;
=1,92;  =3;
=3;  =60%;
=60%;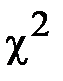 =2,46;
=2,46;  =3;
=3; 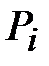 =45%.
=45%. по укрупненному статистическому ряду и подтверждают обоснованность выбора ЗНР для расчета характеристик доремонтной долговечности двигателя.
по укрупненному статистическому ряду и подтверждают обоснованность выбора ЗНР для расчета характеристик доремонтной долговечности двигателя. 



