Определение доверительных границ рассеивания одиночны и средних значений показателя надежности и наибольших возможных ошибок переноса
В результате испытания группы машин и обработки собранной при этом информации определяют количественные характеристики показателей надежности (среднее значение В дальнейшем значения этих характеристик должны быть перенесены (запланированы) на другие группы машин, работающие в других условиях. Естественно, что изменение количества машин в группе и условий их эксплуатации вызовет изменение количественных характеристик ПН. Хотя эти изменения носят случайный характер, они происходят в определенных границах или в определенном интервале, величина которого зависит от многих факторов, в том числе и от количества машин в группе. Определение границ рассеивания характеристик ПН, следовательно, и определение возможной ошибки их переноса из одних условий в другие является одной из основных задач теории надежности. Если было проведено наблюдение за Для нормального распределения площадь под дифференциальной кривой, или площадь охвата α, ограниченная протяженностью оси абсцисс Таким образом, площадь охвата α равна в долях единицы или в процентах количеству одиночных ПН, числовые значения которых укладываются в границах соответствующего этой площади интервала. При прочих равных условиях выбранная заранее площадь охвата α характеризует степень доверия расчета и гарантирует вероятность попадания показателя надежности в соответствующий интервал его значений. Поэтому она называется доверительной вероятностью α. Интервал, в котором при заданной доверительной вероятности α попадают 100 α % от Границы, в которых может колебаться значение одиночного ПН при заданном α, называют нижней доверительной границей При определении коэффициента Рассмотрим уравнения для определения доверительного интервала
Анализ расчетных уравнений (21-24) позволяет заметить, что увеличение доверительной вероятности α или повышение степени доверия расчета вызывает увеличение возможной ошибки расчета Приведем типичный пример расчета доверительных границ одиночного ПН. Порядок расчета следующий. Задаемся доверительной вероятностью: α=0,90. 1. По таблице 7 Приложения находим значения коэффициента 2. По уравнениям (22) и (23) определяем доверительные границы наработок до постановки двигателей в ремонт:
Доверительный интервал
В случае ЗРВ доверительные границы рассеивания одиночного ПН определяют по такой же принципиальной схеме, как и при ЗНР. Однако вследствие асимметрии дифференциальной функции пользование уравнениями (21)-(24). При относительно больших значениях коэффициента вариации (V =0,6-1,0) можно привести к значительным ошибкам. Доверительные границы рассеивания одиночного ПН при ЗРВ определяются по уравнениям:
где Если принять, что рассеивание доремонтных ресурсов двигателей согласуется с ЗРВ (
В практике чаще всего приходится встречаться с расчетом доверительных границ среднего значения ПН Расчетная схема и физический смысл доверительных границ при заданной доверительной вероятности α для среднего значения ПН те же, что и для одиночного показателя. Разница в определении величины среднего квадратического отклонения
По аналогии с расчетными уравнениями (21)-(24) для определения рассеивания среднего значения ПН при ЗНР и заданной доверительной вероятности α будет: абсолютная ошибка:
нижняя доверительная граница:
верхняя доверительная граница:
доверительный интервал:
Порядок расчета следующий. Доверительная вероятность α=1,67 и коэффициент Стьюдента
Из теории надежности известно, что сложение нескольких одинаковых или различных теоретических законов распределения приводит в итоге к закону нормального распределения. Поэтому, когда рассеивание одиночных ПН подчинено ЗРВ, рассеивание средних значений ПН в таких случаях согласуется с законом нормального распределения. Следовательно, доверительные границы рассеивания среднего значения
|

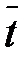 , среднее квадратическое отклонение σ, коэффициент вариации
, среднее квадратическое отклонение σ, коэффициент вариации 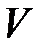 и др.).
и др.).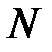 машинами и на этой основе определено среднее значение ПН
машинами и на этой основе определено среднее значение ПН 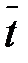 , то, как было показано выше, одиночное значение этого же ПН у конкретной машины может в крайних случаях отличаться от
, то, как было показано выше, одиночное значение этого же ПН у конкретной машины может в крайних случаях отличаться от  на величину
на величину 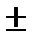 3σ при ЗНР и на величину от 0,1
3σ при ЗНР и на величину от 0,1  до 2,5
до 2,5 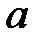 при ЗРВ (
при ЗРВ (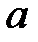 - параметр распределения Вейбулла).
- параметр распределения Вейбулла). -3σ до
-3σ до  +3σ.
+3σ.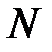 , называют доверительным интервалом
, называют доверительным интервалом 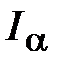 .
. и верхней доверительной границей
и верхней доверительной границей 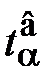 .
. (количество σ) пользоваться интегральным законом нормального распределения и соответственно данными таблицы 1 приложения можно только тогда, когда повторность информации N > 100, вследствие чего опытное значение σ будет незначительно отличаться от теоретического. При меньших значениях повторности информации N следует пользоваться законом распределения Стьюдента и коэффициентом
(количество σ) пользоваться интегральным законом нормального распределения и соответственно данными таблицы 1 приложения можно только тогда, когда повторность информации N > 100, вследствие чего опытное значение σ будет незначительно отличаться от теоретического. При меньших значениях повторности информации N следует пользоваться законом распределения Стьюдента и коэффициентом  , табулированным в таблице 7 приложения.
, табулированным в таблице 7 приложения.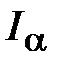 , доверительных границ
, доверительных границ 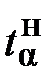 и
и 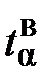 и абсолютной ошибки
и абсолютной ошибки 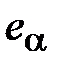 для одиночного показателя надежности при законе нормального распределения:
для одиночного показателя надежности при законе нормального распределения: (21)
(21) (22)
(22)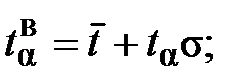 (23)
(23)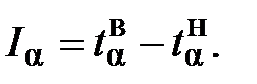 (24)
(24)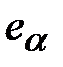 и расширение доверительного интервала. При расчете доверительных границ рассеивания ПН (ГОСТ 17510-72) рекомендуется применять следующие значения доверительных вероятностей: α=0,80;0,90;0,95;0,99.
и расширение доверительного интервала. При расчете доверительных границ рассеивания ПН (ГОСТ 17510-72) рекомендуется применять следующие значения доверительных вероятностей: α=0,80;0,90;0,95;0,99.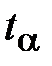 для α=0,90 и
для α=0,90 и 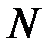 =69:
=69:  =1,67.
=1,67.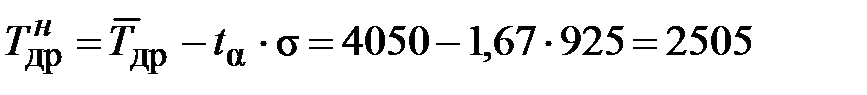 мото-ч;
мото-ч;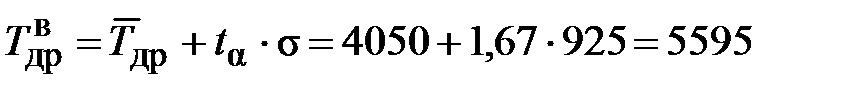 мото-ч.
мото-ч. находим по уравнению (24):
находим по уравнению (24):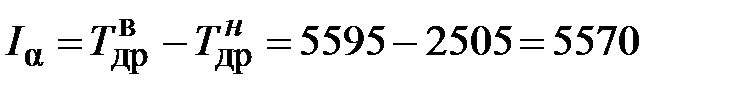 мото-ч.
мото-ч. (25)
(25)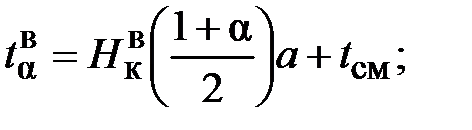 (26)
(26)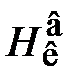 - квантиль ЗРВ, значение которого находят по таблице 8 Приложения (вход в таблицу по величине параметра b и величинам
- квантиль ЗРВ, значение которого находят по таблице 8 Приложения (вход в таблицу по величине параметра b и величинам  или
или 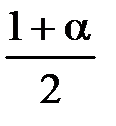 ).
).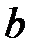 =3,34,
=3,34, 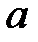 =3080 мото-ч,
=3080 мото-ч, 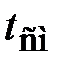 =1250 мото-ч), получим:
=1250 мото-ч), получим: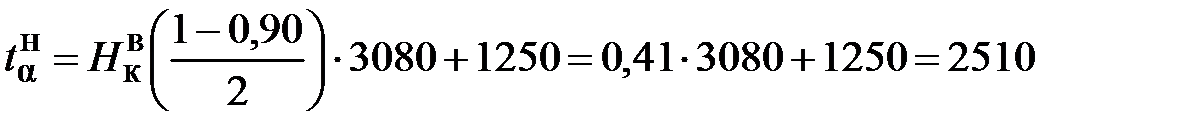 мото-ч,
мото-ч,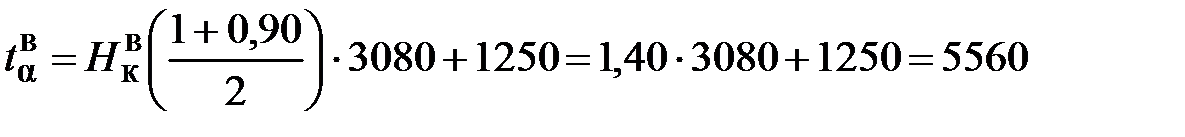 мото-ч.
мото-ч.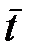 .
. . Связь между
. Связь между 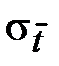 и σ установлена в теории вероятностей:
и σ установлена в теории вероятностей: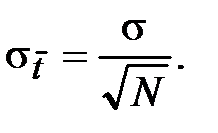 (27)
(27) , (28)
, (28) , (29)
, (29)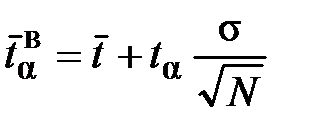 , (30)
, (30) . (31)
. (31)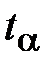 =1,67 (табл. 7 Приложения):
=1,67 (табл. 7 Приложения):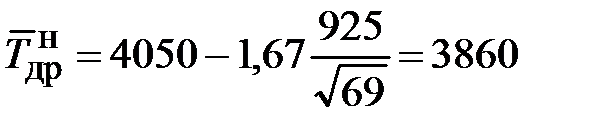 мото-ч;
мото-ч; мото-ч;
мото-ч; при ЗРВ можно определить по уравнениям (29) и (30).
при ЗРВ можно определить по уравнениям (29) и (30).


