Проверка информации на выпадающие точки
В опытной информации о показателях надежности, полученной в процессе наблюдения за машинами, могут быть ошибочные точки, выпадающие из общего закона распределения. Поэтому перед окончательной математической обработкой информацию проверяют на выпадающие точки. Грубую проверку информации проводят по правилу В расчете по двигателям СМД-14 нижняя границы достоверности информации будут соответственно равны: 4140 - 3∙1050 =990 мото-ч (нижняя граница) и 4140 + 3∙1050 = 7290 мото-ч (верхняя граница). Наименьший доремонтный ресурс двигателя Наибольший ресурс двигателя Более точно проверяют как крайние, так и любые другие смежные точки информации по критерию l (критерий Ирвина). Теоретические значения критерия lпри различном количестве информации приведены в таблице 2 приложения. Фактическое значение критерий
где Проверим крайние точки информации о доремонтных ресурсах двигателя СМД-14.
а) для наименьшей точки информации (
б) для наибольшей точки информации (
Сравнение опытных и теоретических (табл. 2 приложения) критериев при Если проверка исключает точки информации, то необходимо вновь перестроить статистический ряд и пересчитать среднее значение и среднее квадратическое отклонение показателя надежности. Учитывая, что последняя точка информации выпала, делаем такой пересчет и в нашем расчете. Пользуясь уравнениями (1), (2),(4) и (5), получим:
В таблице 3 приведен уточненный статистический ряд распределения доремонтного ресурса двигателя СМД-14.
|


 3
3  , т.е. полученное расчетным путем среднее значение показателя надежности последовательно уменьшают и увеличивают на 3s. Если крайние точки информации не выходят за пределы
, т.е. полученное расчетным путем среднее значение показателя надежности последовательно уменьшают и увеличивают на 3s. Если крайние точки информации не выходят за пределы  3
3  , все точки информации действительны.
, все точки информации действительны.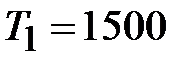 мото-ч (см. табл.1). Следовательно, эта точка информации действительна и должна быть учтена при дальнейших расчетах (1500> 990).
мото-ч (см. табл.1). Следовательно, эта точка информации действительна и должна быть учтена при дальнейших расчетах (1500> 990).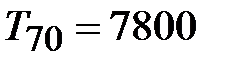 мото-ч. Эта точка информации выходит за верхнюю границу достоверности (7290 мото-ч). Поэтому она не должна учитываться в дальнейших расчетах.
мото-ч. Эта точка информации выходит за верхнюю границу достоверности (7290 мото-ч). Поэтому она не должна учитываться в дальнейших расчетах.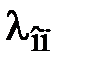 определяют по уравнению:
определяют по уравнению: , (6)
, (6)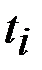 и
и 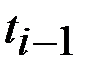 - смежные точки информации.
- смежные точки информации. для крайних точек информации:
для крайних точек информации: мото-ч)
мото-ч) .
.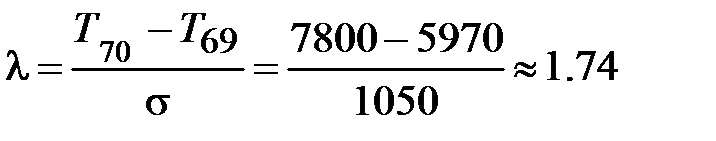 .
. =70 позволяет заключить: первая точка информации
=70 позволяет заключить: первая точка информации  мото-ч является достоверной точкой (
мото-ч является достоверной точкой (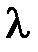 = 0,35 <
= 0,35 <  =1,1), и ее следует учитывать при дальнейших расчетах; последняя точка информации
=1,1), и ее следует учитывать при дальнейших расчетах; последняя точка информации 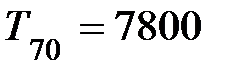 мото-ч представляет собой выпадающую точку (
мото-ч представляет собой выпадающую точку (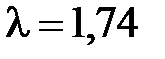 >
>  ), и ее следует исключить из дальнейших расчетов.
), и ее следует исключить из дальнейших расчетов. интервалов;
интервалов; мото-ч;
мото-ч;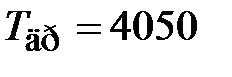 мото-ч;
мото-ч;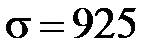 мото-ч.
мото-ч.


