Законы распределения отказов изделий АТ.(случайные велечины)
Одним из основных понятий является - случайное событие. Событием называется всякий факт (исход), который в результате опыта (испытания) может произойти или не произойти. Случайной называют величину, которая в результате испытания может принять одно из возможных заранее неизвестных значений. Случайным величинам противопоставляются величины детерминированные. Случайные величины подразделяются на дискретные (принимающие отдельные значения) и непрерывные. Каждому из таких событий можно поставить в соответствие определенное число, называемое его вероятностью и являющееся мерой возможного совершения этого события. Теория вероятностей основывается на аксиоматическом подходе и опирается на понятия теории множеств. Множество – это любая совокупность объектов произвольной природы, каждый из которых называется элементом множества. Предположим, что производится некоторый опыт (испытание), результат которого заранее неизвестен. Тогда множество В общем случае, если множество Совместные (несовместные) события – такие события, появление одного из которых не исключает (исключает) возможности появления другого. Зависимые (независимые) события – такие события, появление одного из которых влияет (не влияет) на появление другого события. Противоположное событие относительно некоторого выбранного события А – событие, состоящее в не появлении этого выбранного события (обозначается Полная группа событий – такая совокупность событий, при которой в результате опыта должно произойти хотя бы одно из событий этой совокупности. Закон распределения случайных величин указывает на взаимосвязь между возможными значениями случайной величины и их вероятностями. Закон распределения может быть задан аналитически (формулой), в виде таблицы, графиком или диаграммой. Основное свойство любого закона распределения
где Для описания закономерностей, свойственных различным периодам эксплуатации изделий, используют различные законы распределения (табл.1). Так, период нормальной эксплуатации описывается экспоненциальным распределением, играющим важную роль в теории надежности. В качестве модели надежности изделий при возрастающем количестве отказов, связанных с процессами старения и износа элементов конструкций, используют нормальное распределение, при описании процессов приработки изделий — распределение Вейбулла. В случаях, когда закономерности изменения надежности изделий AT не могут быть описаны с помощью рассмотренных распределений, используют другие распределения или ограничиваются непараметрическими методами оценки надежности AT.
|

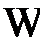 всех возможных исходов опыта представляет пространство элементарных событий, а каждый его элемент
всех возможных исходов опыта представляет пространство элементарных событий, а каждый его элемент  (отдельный исход опыта) является элементарным событием. Любой набор элементарных событий (любое их сочетание) считается подмножеством (частью) множества
(отдельный исход опыта) является элементарным событием. Любой набор элементарных событий (любое их сочетание) считается подмножеством (частью) множества  .
.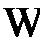 содержит n элементов, то в нем можно выделить
содержит n элементов, то в нем можно выделить 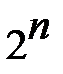 подмножеств (событий).
подмножеств (событий). ).
). ,
,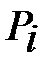 - вероятность значения случайной величины
- вероятность значения случайной величины  .
.


