Задание требований по надежности
Предварительные замечания. При задании требований по надежности следует различать технические объекты трех уровней: 1) системы — технические объекты, выполняющие определенные самостоятельные функции и характеризуемые оперативно-техническими показателями надежности и эффективности функционирования; 2) подсистемы — технические объекты, входящие в состав системы, выполняющие частные функциональные задачи и характеризуемые в основном техническими показателями надежности; 3) элементы — технические объекты, представляющие собой элементную базу подсистем. Задание требований на систему. 1. Экспертное (директивное) задание требований основывается только на общей инженерной интуиции и практическом опыте, а поэтому не требует каких-либо особых комментариев. 2. Задание требований по прототипу основывается на анализе имеющейся статистической информации по надежности уже существующих технических объектов, близких к рассматриваемому по назначению, структуре или элементной базе. Требования по надежности в этом случае задаются с учетом возможного роста надежности элементной базы, масштаба рассматриваемой системы по сравнению с прототипом, условий функционирования и т. п. Такой прогноз в значительной степени также опирается на экспертные оценки, однако подтверждается конкретными фактическими данными. 3. Задание оптимального уровня надежности возникает только в том случае, когда: выходной эффект от функционирования системы измерим в тех же (обычно-стоимостных) единицах, что и затраты на ее создание; достоверно известны исходные данные о надежности элементной базы; полностью определены принципы построения как структуры, так и процессов функционирования (возможность резервирования, использование различной элементной базы, режим использования, регламент технического обслуживания и т. п.). В этом случае задание требований сводится к максимизации целевой функции вида
где
где, в свою очередь, m — число рассматриваемых вариантов структуры, а n — число различных комплектующих элементов;
Для всякого фиксированного k решение находится обычным способом из условия
после чего выбирается вариант, для которого достигается наибольшее абсолютное значение из оптимальных решений Если выходной эффект системы несоизмерим с затратами (объекты обороны, системы безопасности различных транспортных средств и т.п.), то задание требований по надежности на систему возможно только двумя первыми способами. Задание требований на подсистему. Предполагается, что требования на подсистему задаются при наличии уже каким-то образом заданных требований на систему в целом. 1. Метод равномерного распределения. Если система состоит из N примерно близких по сложности (т. е. по структуре и числу входящих элементов) подсистем, то можно заданный показатель надежности (R) типа вероятности безотказной работы, коэффициента оперативной готовности или коэффициента готовности распределять по правилу
Задаваемая средняя наработка для i -й подсистемы в этом случаеприближенноравна 2. Метод пропорционального распределения. Если
Под 3. Метод оптимального распределения. Если при задании требований по надежности на систему в целом (R) известны структура системы (S) и методы повышения надежности подсистем, т. е. функции а) максимум показателя надежности системы при ограничениях на суммарный ресурс б) минимум затрат на систему при достижении заданного показателя надежности Обе задачи решаются обычными способами дискретного программирования, как задачи на условную оптимизацию.
|

 ,
, — показатель надежности системы, зависящий от выбранного
— показатель надежности системы, зависящий от выбранного  -то варианта структуры системы
-то варианта структуры системы  и от надежности элементов
и от надежности элементов  -го типа
-го типа  , т. е.
, т. е. ,
, — выходной эффект от функционирования k -то варианта системы в стоимостном выражении при уровне надежности R;
— выходной эффект от функционирования k -то варианта системы в стоимостном выражении при уровне надежности R;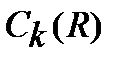 — затраты на обеспечение уровня надежности, равного R, для k -гo варианта системы.
— затраты на обеспечение уровня надежности, равного R, для k -гo варианта системы. ,
, .
.
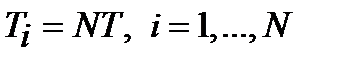 , Е — заданная средняя наработка системы.
, Е — заданная средняя наработка системы.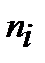 — число элементов в i -й подсистеме, то
— число элементов в i -й подсистеме, то
 в данном случае следует понимать число в некотором смысле «приведенных» элементов.
в данном случае следует понимать число в некотором смысле «приведенных» элементов. , где
, где  — ресурс, затрачиваемый на обеспечение надежности подсистемы, то можно найти оптимальное распределение требований по надежности для двух случаев:
— ресурс, затрачиваемый на обеспечение надежности подсистемы, то можно найти оптимальное распределение требований по надежности для двух случаев: ,
,



