Диаграммы равновесия жидкость – пар в бинарных системах. Первый закон Коновалова. Фракционная перегонка
На рис.5,6,7 общее давление пара бинарного раствора было представлено как функция состава раствора. В качестве аргумента можно также использовать состав пара, определяемый кривыми парциальных давлений и отличающийся от состава жидкого раствора. Таким путем можно получить вторую кривую того же свойства системы – общего давления насыщенного пара раствора в зависимости от другого аргумента – состава пара. На рис.8 изображена схематическая диаграмма – изотерма равновесия бинарный раствор – пар. Любая точка на плоскости диаграммы характеризует валовый состав системы (координата х) идавление (координата P) и называется фигуративной точкой. Верхняя кривая отображает зависимость давления насыщенного пара от состава жидкости, а нижняя кривая – зависимость давления насыщенного пара от состава пара. Этими кривыми плоскость диаграммы разделяется на три поля. Верхнее поле охватывает значения х и P, при которых существует только одна жидкая фаза – раствор переменного состава. Нижнее поле отвечает газовой смеси переменного состава. Любая фигуративная точка в верхнем и нижнем полях изображает состояние одной реально существующей фазы. Поле, заключенное между двумя кривыми, соответствует двухфазной системе. Система, давление и состав которой отображает фигуративная точка, находящаяся в этом поле, состоит из двух фаз – раствора и насыщенного пара. Состав этих фаз определяется координатами точек, лежащих на пересечении изобары, проходящей через фигуративную точку системы, с верхней и нижней кривыми. Например, система, характеризуемая фигуративной точкой k, состоит из двух равновесных фаз, состав которых определяется точками а и b. Точка а, лежащая на нижней кривой, характеризует состав насыщенного пара, а точка b, лежащая на верхней кривой,– состав раствора. Нижняя кривая называется ветвью пара, верхняя кривая – ветвью жидкости.
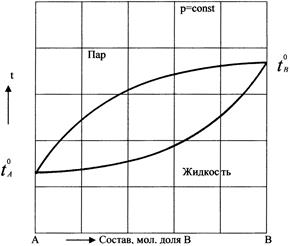
Рис.8. Диаграмма состав – давление бинарной системы. При изотермическом сжатии ненасыщенного пара состава х 1фигуративная точка системы движется вверх по вертикали, конденсация пара начинается в точке а (рис.8) при известном значении давления P. Первые капли жидкости имеют состав х 2;образовавшаяся жидкость содержит меньше компонента А, чем конденсирующийся пар. При изотермическом уменьшении давления жидкость состава х 3начнет испаряться в точке d, давая пар состава x 4 (точка е); образовавшийся пар содержит больше компонента А, чем испаряющаяся жидкость. Следовательно, в паре всегда преобладает по сравнению с равновесной с ним жидкостью компонент А, прибавление которого к системе, как это видно из диаграммы, увеличивает полное давление пара. На основании сказанного легко можно сделать следующее заключение: насыщенный пар по сравнению с равновесным раствором относительно богаче тем компонентом, добавление которого к системе повышает полное давление пара. Это – первый закон Коновалова (1881), являющийся справедливым для всех устойчивых растворов. Рассмотрим явления испарения и конденсации растворов также с помощью изобарной диаграммы температура кипения – состав раствора. Диаграммы t кип. – х можно построить по экспериментальным данным, или имея ряд изотермических диаграмм P – х. На каждой диаграмме P – х, построенной при определенной температуре, находят составы сосуществующих раствора и пара при заданном давлении. По полученным из всех изотерм P – х данным для определенного давления строят одну изобарную диаграмму t кип. – х. Диаграмма t кип. – х показана схематически на рис.9. Так как компонент А с более высоким давлением насыщенного пара Верхнее поле на диаграмме t кип. – х отвечает пару, а нижнее – жидкости. Верхняя кривая – ветвь пара, а нижняя кривая – ветвь жидкости.
Рис.9. Диаграмма температура кипения – состав бинарной системы.
В ректификационных колоннах последовательные перегонки объединены в один автоматизированный процесс, приводящий к разделению компонентов жидкого раствора (ректификация). Промышленное разделение нефти на фракции (первичная переработка нефти) основано на указанном процессе. В заключение приведем еще одну формулировку первого закона Коновалова: В насыщенном паре, находящемся в равновесии с жидким бинарным раствором, выше относительное содержание того компонента, который при T = const имеет более высокое значение давления насыщенных паров по сравнению с другим компонентом или при P = const имеет по сравнению с ним более низкую температуру кипения, иначе говоря, пар по сравнению с жидкостью относительно богаче более летучим компонентом.
|


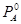 (рис.8) имеет при данном давлении более низкую температуру кипения (
(рис.8) имеет при данном давлении более низкую температуру кипения (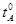 ), то диаграмма t кип. – х имеет зеркально-подобный вид по отношению к диаграмме P – х (имеется только качественное подобие).
), то диаграмма t кип. – х имеет зеркально-подобный вид по отношению к диаграмме P – х (имеется только качественное подобие).