Метод Гаусса
Суть этого метода состоит в том, что посредством последовательного исключения неизвестных матрица системы превращается в треугольную, равносильную данной. Удобнее приводить к трапециевидному виду расширенную матрицу системы, выполняя элементарные преобразования над ее строками. Пример. Решить систему уравнений методом Гаусса: x1 + x2 – 3x3 = 2, 3x1 – 2x2 + x3 = - 1, 2x1 + x2 – 2x3 = 0. Решение. Выпишем расширенную матрицу данной системы и произведем следующие элементарные преобразования над ее строками: а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2: б) третью строку умножим на (-5) и прибавим к ней вторую: В результате всех этих преобразований данная система приводится к треугольному виду: x1 + x2 – 3x3 = 2, -5x2 + 10x3 = -7, - 10x3 = 13. Из последнего уравнения находим x3 = -1,3. Подставляя это значение во второе уравнение, имеем x2 = -1,2. Далее из первого уравнения получим x1 = - 0,7.
|

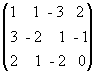
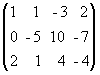 ;
; .
.


