Прямая задача теории погрешностей
Основная задача теории погрешностей состоит в том, чтобы определить по известным погрешностям параметров погрешность функции от этих параметров. Пусть задана дифференцируемая функция
При зависимости функции от одного параметра:
Предельной абсолютной погрешностью функции называют следующую оценку погрешности величины
Пусть задана дифференцируемая функция
Предельной относительной погрешностью функции называю величину Рассмотрим частные случаи. Предельная абсолютная погрешность суммы равна сумме предельных абсолютных погрешностей слагаемых:
Формула дает максимально возможное значение предельной абсолютной погрешности суммы, которое достигается, если погрешность каждого слагаемого принимает наибольшее из возможных значений, и погрешности всех слагаемых имеют одинаковые знаки. При большом количестве слагаемых такое неблагоприятное стечение обстоятельств маловероятно. Погрешности отдельных слагаемых, как правило, имеют различные знаки и частично компенсируют друг друга. Предельная относительная погрешность суммы оценивается следующим образом:
Пусть
Если все числа Остановимся на вычислении предельной относительной погрешности разности. Пусть
При малой абсолютной погрешности близких чисел Погрешность степенного выражения
Зная Отметим несколько полезных следствий из полученной формулы: 1. Предельная относительная погрешность произведения равна сумме предельных относительных погрешностей сомножителей 2. 3. 4.
|

 и пусть
и пусть  - абсолютные погрешности аргументов. Тогда абсолютная погрешность функции (формула Лагранжа):
- абсолютные погрешности аргументов. Тогда абсолютная погрешность функции (формула Лагранжа):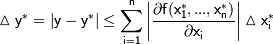
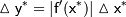
 :
:
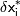 - относительные погрешности аргументов. Тогда относительная погрешность функции:
- относительные погрешности аргументов. Тогда относительная погрешность функции: или
или 
 .
.

 , а
, а  , тогда:
, тогда:
 одного знака (арифметическая сумма), и относительная погрешность удовлетворяет неравенству
одного знака (арифметическая сумма), и относительная погрешность удовлетворяет неравенству  становится очевидным, что для повышения точности суммы в первую очередь необходимо уточнить слагаемые с наибольшей относительной погрешностью. (Андреев-8)
становится очевидным, что для повышения точности суммы в первую очередь необходимо уточнить слагаемые с наибольшей относительной погрешностью. (Андреев-8)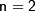 и числа
и числа 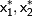 разных знаков, тогда:
разных знаков, тогда:
 расчитывается следующим образом:
расчитывается следующим образом:
 , предельную абсолютную погрешность можно найти по формуле
, предельную абсолютную погрешность можно найти по формуле 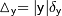 .
. ,
,  . При умножении приближенного числа на точный множитель
. При умножении приближенного числа на точный множитель  предельная относительная погрешность приближенного числа не меняется
предельная относительная погрешность приближенного числа не меняется  , а предельная абсолютная погрешность увеличивается в
, а предельная абсолютная погрешность увеличивается в  раз \vartriangle _{y}.
раз \vartriangle _{y}. ,
,  . Предельная относительная погрешность степени приближенного числа умножается на показатель степени
. Предельная относительная погрешность степени приближенного числа умножается на показатель степени  .
. Предельная относительная погрешность корня из приближенного числа делится на показатель корня
Предельная относительная погрешность корня из приближенного числа делится на показатель корня  .
.


