Множественный регрессионный анализ

В общем случае в регрессионный анализ вовлекаются несколько независимых переменных. Это, конечно же, наносит ущерб наглядности получаемых результатов, так как подобные множественные связи в конце концов становится невозможно представить графически.

В случае множественного регрессионного анализа речь идёт необходимо оценить коэффициенты уравнения

у = b₁-х₁+b₂-х₂+... + b_n-х_n+а,

где n — количество независимых переменных, обозначенных как х₁ и х_n, а — некоторая константа.

Переменные, объявленные независимыми, могут сами коррелировать между собой; этот факт необходимо обязательно учитывать при определении коэффициентов уравнения регрессии для того, чтобы избежать ложных корреляций.

При работе с множественной регрессией, в отличие от парной, необходимо определять алгоритм анализа. Стандартный алгоритм включает в итоговую регрессионную модель все имеющие предикторы. Пошаговый алгоритм предполагает последовательное включение (исключение) независимых переменных, исходя из объяснительного «веса». Пошаговый метод хорош, когда имеется много независимых переменных; он «очищает» модель от откровенно слабых предикторов, делая ее более компактной и лаконичной.

Дополнительным условием корректности множественной регрессии (наряду с интервальностью, нормальностью, линейностью) является отсутствие мультиколлинеарности – наличия сильных корреляционных связей между независимыми переменными.

 

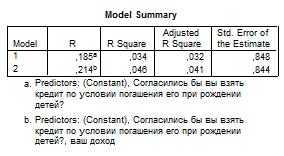
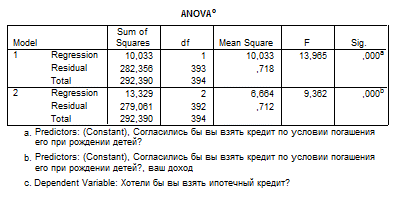
Проведем множественный регрессионный анализ зависимой переменной «желание взять ипотечный кредит» (var1) и независимыми переменными «общая площадь жилья» (S), «возможность кредита при условии его погашения при рождении детей» (A), «доход» (D).

· Выберите в меню Analyze... (Анализ) Regression...(Регрессия) Linear... (Линейная)

Поместите переменную var1 в поле для зависимых переменных, объявите переменные: ««общая площадь жилья», «согласие на кредит, при условии погашения его при рождении детей», «доход» независимыми. В меню Method установлен по умолчанию – Enter (Включение), соответствующий стандартному алгоритму. Этот метод соответствует одновременной обработке всех независимых переменных, выбранных для анализа, и поэтому он может рекомендоваться для использования только в случае простого анализа с одной независимой переменной.

Для множественного анализа следует выбрать один из пошаговых методов. При выборе пошагового алгоритма в списке Method – Forward (Прямой) – пошаговое включение переменных с проверкой на значимость их частной корреляции с критерием. В результате в уравнение включаются все переменные, имеющие значимую частную корреляцию с переменной-критерием. Включение производится в порядке возрастания р-уровня.

При выборе Backward (Обратный) – пошаговый метод, сначала включающий в уравнение регрессии все независимые переменные, а затем поочередно удаляющий все переменные, чья корреляция с критерием имеет уровень значимости выше заданного порогового значения. Как правило, пороговым значением является р=0,1.

При выборе Stepwise (По шагам) – комбинация пошаговых методов Forward (Прямой) и Backward (Обратный). Основная идея – изменение доли влияния независимой переменной на критерий при появлении в уравнении других независимых переменных. Если влияние какой-либо из включенных переменных становится слишком слабым, то она исключается из уравнения. Подобный метод используется в регрессионном анализе наиболее часто.

Применим его к нашему случаю.

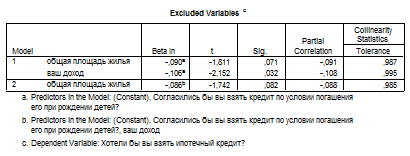
Как видно из таблиц, переменная «общая площадь жилья» исключается из анализа. Значимыми переменными остаются «доход» и «согласие взять кредит при условии погашения его при рождении детей». Переменная «уровень дохода» отрицательно влияет на желание взять ипотечный кредит, возможности взять ипотечный кредит в большей степени рассматривают респонденты с небольшим доходом.

 

Уравнение регрессии для прогнозирования значения var1 (возможность взять ипотечный кредит) выглядит следующим образом:

Var1 = 0,184*A – 0,78*D + 1,712

 

Важным моментом является анализ остатков, то есть отклонений наблюдаемых значений от теоретически ожидаемых. Остатки должны появляться случайно (то есть не систематически) и подчиняться нормальному распределению. Это можно проверить, если с помощью кнопки Charts... (Диаграммы) построить гистограмму остатков.

Проверка на наличие систематических связей между остатками соседних случаев (что, однако, является уместным только при наличии так называемых данных с продольным сечением), может быть произведена при помощи теста Дарбина-Ватсона (Durbin-Watson) на автокорреляцию. Этот тест вычисляет коэффициент, лежащий в диапазоне от 0 до 4. Если значение этого коэффициента находится вблизи 2, то это означает, что автокорреляция отсутствует. Тест Дарбина-Ватсона можно активировать через кнопку Statistics (Статистические характеристики).

Ещё одной дополнительной возможностью является задание переменной отбора в диалоговом окне Linear Regression (Линейная регрессия). Здесь, с помощью кнопки Rule... (Правило) в диалоговом окне Linear Regression: Define Selection Rule (Линейная регрессия: ввод условия отбора), Вы получаете возможность при помощи избирательного признака сформулировать условие, которое будет ограничивать количество случаев, вовлеченных в анализ.