Серьга,
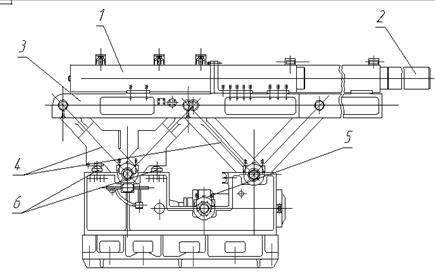
Гидроцилиндр поворота люльки, Плита, 4 – люлька, 5 – гидроцилиндр выдвижения гильзы, 6 – гильзу, 7 – пружинные упоры. Стол подъемно-поворотный предназначен для поворота рулона в положение, удобное для размотки, при котором образующая рулона перпендикулярна оси стана. После остановки рулона над подъемно - поворотным столом, включением гидропривода подъема стола производится подъем стола с рулоном, и освобождается штанга кантователя. Подъем стола производится до уровня, достаточного для ввода внутрь рулона штыря задающего устройства. После вывода из рулона штанги кантователя включением сервопривода стол разворачивается в зависимости от направления навивки в правую или левую сторону. В рулон вводится штырь задающего устройства, после чего подъемно – поворотный стол опускается, оставляя рулон на штыре. Работа подъёмно-поворотного стола проходит с участием как гидроцилиндра, так и гидромеханического привода поворота призмы.
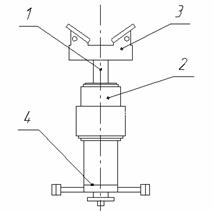
1. Шток подъёма призмы 2. Гидроцилиндр подъёма призмы 3. Призма 4. Гидромеханический привод поворота призмы Устройство задающее предназначено для съема и передачи рулона с подъемно – поворотного стола и передачи его на подъемный стол тележки разматывателя при нахождении ее на первой позиции. Устройство задающее состоит из качающейся рамы, на которой установлен гидроцилиндр перемещения штыря. После опускания подъемно-поворотного стола включением гидропривода перемещается качающая рама со штырем и переносит рулон к подъемному столу тележки разматывателя. Стол тележки разматывателя поднимается и снимает рулон со штыря. Рама и штырь возвращается в исходное положение и цикл повторяется.
1. Гидроцилиндр 2. Штанга 3. Рама 4. Рычаг 5. Гидроцилиндр перемещения рамы 6. Пружинные упоры Со штыря устройства задающего рулон устанавливается на ролики подъемно - поворотного стола. Последний поднимает рулон, освобождая штырь устройства задающего. Затем штырь выводят из рулона, и тележка перемещается на позицию 2. Одновременно с перемещением тележки роликами подъемно-поворотного стола рулон поворачивается в положение, удобное для отгибки конца полосы. После остановки тележки на позиции 2 включается гидропривод фиксатора. Подъемно-поворотным столом рулон поднимается до упора в верхний прижимной ролик. Скребок отгибает конец полосы и зажимает его между приводным роликом и холостым, установленным на скребке. Включением приводного ролика и роликов подъемно-поворотного стола конец полосы передается на проводки, задающие и далее на в разделительно-задающее устройство. Полоса останавливается, конец ее зажимается и удерживается разделительно - задающей машиной до полной размотки рулона. После окончания размотки предыдущего рулона разводятся конуса разматывателя и фиксаторы, затем тележка перемещается в позицию 3. Одновременно конец полосы задается в правильную машину. На позиции 3 рулон устанавливается в конусах разматывателя, а тележка возвращается на позицию 1. Разделительно-задающая машина предназначена для задачи полосы в правильную машину. Машина представляет собой два ролика, собранных на раме с проводкой. Верхний не приводной ролик – для зажима полосы, нижний ролик приводной. Центровка полосы в машине осуществляется, посредством левой и правой кареток с вертикальными роликами, которые при помощи пневмоцилиндра и системы реек равномерно сближаются и центрируют полосу по оси агрегата. Настройка центрирующих роликов на заданную ширину полосы осуществляется перемещением каретки пневмоцилиндра электродвигателем через червячный редуктор и винтовую передачу. Листоправильная машина с тянущими роликами предназначена для правки рулонной ленты. Машина состоит из следующих узлов и механизмов: узел станины; ролики рабочие; ролики опорные; ролик направляющий; ролики тянущие. Тянущие ролики предназначены для задачи ленты в машину. Они вмонтированы в общую станину с рабочими роликами. Верхний ряд рабочих роликов устанавливается на ползуне, который перемещается в направляющих верхней станины и удерживается пружинными подвесками. Для определения величены хода ползуна, устанавливается указатель величины хода. Для уменьшения прогиба рабочих роликов последние опираются на опорные В схему привода листоправильной машины помимо редуктора входит и шестеренная клеть
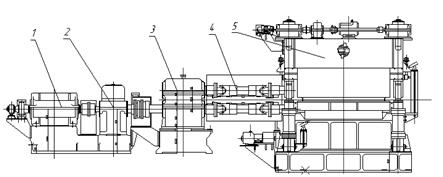
1. Электродвигатель 2. Редуктор 3. Шестерённая клеть 4. Шпиндель 5. Рабочая клеть
Расчет тягового усилия и мощности привода приемного конвейера
Рассчитать тяговое усилие цепного конвейера при следующих данных: вес рулона G=30 т, длина конвейера (расстояние между приводными и натяжными звездочками) L=18,8 м, расстояние между цепями l=1,2 м, число цепей z=2.
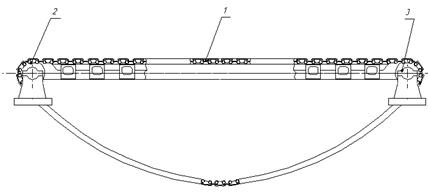
Рисунок 3. Общий вид приемного конвейера. (1-цепи конвейера, 2-ведущие звездочки, 3-ведомые звездочки)
В качестве тягового элемента принимаем катковую цепь с шагом звена t=200 мм, шагом по зацеплению tц=400 мм и массой одного погонного метра цепи qц=24,6 кг (по таблице ІІІ.12 «Цепи тяговые пластинчатые по ГОСТ 588-64» –[1] стр. 172) Погонная нагрузка от веса груза на цепь
Натяжение цепи в точке сбегания с приводной звездочки от провисающего участка
где: λ=18,8 м – длина свободно висящего участка цепи; δ – величина провисания цепи.
Натяжение цепи по точкам перегиба контура конвейера
где ω=0,017 – коэффициент сопротивления движению цепи (по таблице 7.11 –[1] стр.119)
где k=2 – коэффициент сопротивления на звездах
Тяговое усилие на приводных звездочках
Расчетная мощность привода
где η=0,94 – к. п. д. привода 2– число приводов.
Кинематический расчет привода с червячно-цилиндрическим редуктором.
Кинематический расчет привода состоит из следующий основных частей: определения общего передаточного числа; разбивка общего передаточного числа по ступеням; определение кинематической погрешности.
Рисунок 3 – Кинематическая схема червячно-цилиндрического редуктора
Общие рекомендации к расчету
Вращающий момент передается от электродвигателя входному валу редуктора через муфту и частота вращения входного вала равна частоте вращения вала электродвигателя. Редуктор двухступенчатый: на первой ступени: глобоидная червячная передача; на второй ступени: цилиндрическая зубчатая, колеса которой имеют кругловинтовые зубья. Двухступенчатых червячно-цилиндрический редуктор имеет оптимальную конструкцию, большой диаметр ведомого элемента (колеса) цилиндрической передачи излишне увеличивает ширину корпуса редуктора. Поэтому передаточное число цилиндрической и червячной передачи рекомендуется назначать в пределах uчерв= 3,15-5, uцил= 8-40. Кинематическая цепь привода: электродвигатель – червячная передача – цилиндрическая передача, то есть uобщ = uр = u1,2 u3,4 где uр – общее передаточное число редуктора; u1,2 – передаточное число червячной передачи; u3,4 – передаточное число цилиндрической передачи. Привод содержит три вала, частота вращения которых: nэд= nвх – частота вращения вала электродвигателя и входного, частота вращения червяка; nпр - частота вращения промежуточного вала, частота вращения червячного колеса и шестерни; nвых - частота вращения выходного вала, частота вращения зубчатого колеса. Потери мощности, оцениваемые КПД, учитываются в следующих узлах привода: подшипниках входного вала, зацеплении пары цилиндрических колес, подшипниках промежуточного вала, зацеплении червячной передачи, подшипниках выходного вала, то есть
Выбор электродвигателя Исходными данными при выполнении кинематического расчета являются кинематическая схема привода и электродвигатель ДП-810 со следующими параметрами: мощность N=29кВт; напряжение U= 220В частота вращения n=590 об/мин. Определяем потребную мощность привода по формуле:
где W0 – тяговое усилие конвейера; ηприв – КПД привода, который равен
По таблице 6 стр. 28 [1] определяем диапазон значений КПД.
Определяем КПД червячной передачи:
где uчерв – передаточное отношение червячной передачи (ориентировочно принимаем uр=265, uцил=5,6, uчерв= 47)
Кинематический расчет
Определяем общее передаточное число привода:
Разбиваем общее передаточное число по ступеням. От разбивки общего передаточного числа в двухступенчатых редукторах в значительной степени зависят удобство смазывания колес и компоновки деталей, а также конструкция конуса и его габариты. Универсальной рекомендации по разбивке общего передаточного числа по ступеням, удовлетворяющей всем указанным условиям, не существует. Выбор способа разбивки зависит от конкретных требований, которым должна отвечать конструкция: обеспечения минимальных габаритов редуктора, минимальной массы зубчатых колес, получения одинакового погружения зубчатых колес всех ступеней в масляную ванну, создание устойчивости наименьшей площади корпуса редуктора. При разбивки воспользуемся рекомендациями таблицы 12 стр. 35 [1] для червячно-цилиндрического редуктора, согласно которым uт =3,15-5 Принимаем uт =5.
Из стандартного ряда (таблица 10 стр. 32 [1]) назначаем uчерв = 50. Находим фактическое передаточное число редуктора:
Рассчитываем кинематическую погрешность. Оценка погрешности кинематического расчета редуктора заключается в расчете ошибки фактического передаточного числа относительно номинального.
Поскольку при [u]=5% выполняется условие
Расчеты частот, мощностей и вращающих моментов на отдельных элементах привода.
Определяем частоты вращения на валах:
Рассчитываем мощности, передаваемые отдельными элементами привода:
Находим вращающие моменты:
Результаты расчетов заносим в таблицу.
Таблица 2 - Результаты кинематического расчета.
Расчет червячной передачи
Анализируя назначение привода, полагаем, что передача установлена в слабо вентилируемом помещении со средней температурой воздуха t0=200C. Его основная цель – определение межосевого расстояния передачи из условия контактной выносливости зубьев колеса.
Проектировочный расчет
Выбор материала зубьев колеса производится в зависимости от величины скорости скольжения в зацеплении, твердости и чистоты поверхности витков червяка. Определяем скорость скольжения:
По таблице 44 стр. 178 [1] и таблице 45 стр. 180 [1] назначаем:
для червяка – сталь 45 закаленную ТВЧ до твердости 50 HRC с последующей шлифовкой и полировкой витков, для колеса – безоловянную бронзу Бр А9ЖЗЛ с отливкой в кокиль. Так как венец червяка колеса выполнен из безоловянной бронзы, принимаем KHL=1. Рассчитываем допускаемые контактные напряжения:
Предварительно назначаем по таблице 52 стр. 192 [1] для uном=50 коэффициент диаметра червяка, который может иметь значения: 12,5 и 20. Наиболее часто повторяется значение 12,5. Поэтому q = 12,5 наиболее вероятно. При этом отношение
Находится в рекомендованных пределах Рассматриваем коэффициент нагрузки:
где Кv – коэффициент динамичности равный 1,0-1,3 при υs = 1,5-7,5 м/с, принимаем Кv =1,2; Кβ – коэффициент неравномерности распределения нагрузки по длине контактной линии равный 1,03-1,1, при q=12,5 принимаем Кβ = 1,05.
Рассчитываем потребное межосевое расстояние:
где КаТ’=310 МПа1/3 по таблице 47 стр. 184 [1].
Принимаем из стандартного ряда по таблице 46 стр. 183 [1] ачерв=500 мм. По таблице 52 стр. 192 [1] назначаем параметры передачи: Z1=1; Z2=50; m=16; q=12.5; x=0; u=50. Рассчитываем остальные геометрические и конструктивные параметры передачи: для червяка:
для колеса:
Проверка:
Принимаем следующие формулы из таблицы 53 стр. 198 [1].
Принимаем b1=248 мм, так как для шлифованных червяков b1 увеличивается на (35-40) мм при m=10-16.
В соотве6тствии с таблицей 54 стр. 199 [1] назначаем 8 степень точности передачи по СТ СЭВ 311-76.
Проверочный расчет
Его основная цель – определение контактных напряжений при окончательно принятых параметрах передачи. Эти напряжения не должны превышать напряжений допускаемых. Определяем фактическую частоту вращения колеса:
Рассчитываем угол подъема витков червяка:
Находим фактическую скорость скольжения:
Следовательно, материал колеса выбран правильно. Определяем КПД червячного зацепления:
где ρ’=20 по таблице 49 стр. 188 [1].
Ранее было принято КПД равный 0,69. Полученное отклонение равно нулю. Принимаем коэффициент долговечности по условию контактной прочности КHL=1 и коэффициент долговечности по условию изгибной выносливости зубьев колес КFL=1,4. Допускаемые напряжения: контактные [σ]H=160 МПа; изгибные [σ]F=58 МПа. Определяем допускаемые напряжения с учетом режима работы передачи:
Уточняем коэффициенты расчетной нагрузки:
где КV – коэффициент динамичности, Кβ – коэффициент неравномерности распределения нагрузки по длине контактной линии. Принимаем КV =1,2
По таблице 55 принимаем θ=157 и х=0,74.
Рассчитываем контактные напряжения:
где ZM – коэффициент, учитывающий механические свойства материалов спряженных зубчатых колес, принимаем по таблице 21 стр. 72 [1]; ZH – коэффициент учитывающий форму сопряженных поверхностей зубьев, для прямозубой передачи Принимаем ZM =8600МПа ½
Сравниваем с допустимым значением:
165,7 МПа > 160МПа
Определяем перегруз, который не должен превышать допустимый:
Контактная усталостная прочность обеспечена, так как допускается перегрузка по контактным напряжениям до 5% из рекомендаций. Определяем расчетные изгибные напряжения:
где YF – коэффициент формы зуба червячного колеса. По таблице 48 стр. 185 [1], принимаем YF =1,45, что соответствует числу зубьев эквивалентного колеса:
Сравниваем с допустимым значением:
23,95 МПа < 81 МПа
Изгибная усталостная прочность обеспечена. Проверяем передачу на статическую прочность при кратковременных перегрузках:
где Кпер – коэффициент перегрузки
Определяем допускаемые напряжения изгиба при статической перегрузке передачи:
Для бронзы БрА9ЖЗЛ σВ=490 МПа.
Сравниваем с допустимым значением:
50,5 МПа < 294 МПа Статическая изгибная прочность при перегрузках обеспечена. Проверяем передачу на теплостойкость:
Определяем рабочую температуру масла:
где Кt – коэффициент теплопередачи; St – площадь поверхности теплоотдачи. Принимаем t0=200С, Кt=20 кВт/м2 0С – охлаждение искусственное обдувом воздухом по таблице 50 стр. 189 [1], F/Fн=0,4. Под площадью поверхности теплоотдачи понимается внешняя часть корпуса, которая омывается или обрызгивается изнутри маслом. Если для увеличения внешней поверхности на корпусе сделаны ребра, выступы, бобышки, в состав теплоотдающей поверхности включается только 70 % их внешней площади.
Сравниваем с допустимым значением:
47,60С <600С
Теплостойкость передачи обеспечена.
Расчет зубчатой передачи
Проектировочный расчет
Основной задачей является назначение материалов и расчет напряжений. Принимаем для изготовления шестерни и колеса Сталь 45 с термообработкой – улучшение. Обоснование: зубья нарезают после термообработки заготовки. При этом достигается достаточная твердость изготовления зубчатых колес без использования дорогих финишных операций. Колеса хорошо прирабатываются. По таблице 26 стр. 87 [1] и по таблице 27 стр. 88 [1] выбираем: для шестерни: твердость поверхности зубьев Н1=269-302 НВ (наиболее вероятная твердость 285 НВ); σВ1=890 МПа; σТ1=650 МПа; для колеса: твердость поверхности зубьев Н2=235-262 НВ (наиболее вероятная твердость 250 НВ); σВ2=780 МПа; σТ2=6540 МПа;
Определяем допускаемые контактные напряжения:
где σHlimb – предел контактной выносливости; SH – коэффициент безопасности; KHL – коэффициент долговечности; ZR – коэффициент, учитывающий шероховатость сопряженных поверхностей; ZV – Коэффициент, учитывающий влияние окружной скорости; KL – коэффициент, учитывающий влияние смазки; KXH – коэффициент, учитывающий влияние размера колеса. По таблице 28 стр. 90 [1] принимаем: для шестерни:
По таблице 29 стр. 91 [1] принимаем SH=1,1; КHL=1; ZR=1; ZV=1; KL=1; KXH=1.
для колеса:
По таблице 29 стр. 91 [1] принимаем SH=1,1; КHL=1; ZR=1; ZV=1; KL=1; KXH=1.
За расчетное допускаемое контактное напряжение для прямозубой цилиндрической передачи принимаем меньшее из [σ]H1 и [σ]H2 - [σ]рас=518 МПа. Назначаем коэффициенты: Принимаем коэффициент ширины зубчатого колеса ψba=0,315 по таблице 30 стр. 94 [1]. А так же по таблице 37 стр. 105 [1] КНβ=1,15 при b2/d1=0,945 и условии, что колеса прирабатываются и находятся вблизи одной из опор; а для прямых зубьев принимаем КНα=1. По таблице 38 стр. 106 [1] принимаем KHV=1,2. Определяем межосевое расстояние:
где Кар – средний суммарный коэффициент, по таблице 22 принимаем равным 9,75 103 МПа1/3; КНβ - коэффициент распределения нагрузки по ширине колеса; КНα- коэффициент, учитывающий распределение нагрузки между зубьями; KHV - коэффициент динамического нагружения зубьев; ψba - коэффициент ширины зубчатого колеса.
Принимаем по таблице 32 стр. 98 [1] стандартное значение а=1000 мм. Назначаем модуль:
Принимаем модуль из ряда значений по СТ СЭВ 310-76 равный 10. Для силовых передач рекомендуется принимать модуль из условия обеспечения повышения плавности работы передачи.
Назначаем числа зубьев:
Определяем фактическое передаточное число:
Определяем процент ошибки, который не должен превышать 5%:
Рассчитываем геометрические размеры зубчатых колес:
Принимаем по таблице 34 стр. 100 [1] из ряда нормальных линейных размеров b2=320 мм.
Проверка:
Назначаем степень точности:
Одним из основных показателей качества зубчатых колес является их точность. Точность изготовления зубчатых колес и передач означает не только их кинематические и эксплуатационные показатели, а и такие характеристики как интенсивность шума и вибрации, а также существенно влияет на показатели прочности передачи, долговечность ее работы, потери на трение и т. д. По нормам кинематической точности, плавности работы и контакта зубьев зубчатые передачи делят на 12 ступеней точности. Основанием для назначения степени точности зубчатых колес рассчитываемой передачи является окружная скорость.
Определяем окружную скорость:
По таблице 35 стр. 103 [1] и по таблице 36 стр. 104 [1] назначаем степень точности – 9 ГОСТ 1643-81.
Проверочный расчет Преследует цель проверить работоспособность передачи по все возможным критериям работоспособности. Неудовлетворительные результаты хотя бы одной проверки требуют изменение параметров передачи. Проверяем на контактную усталостную прочность:
Zε – коэффициент, учитывающий суммарную длину контактных линий
здесь εα – торцевой коэффициент перекрытия
ZH – коэффициент учитывающий форму сопряженных поверхностей зубьев, для прямозубой передачи принимаем равным 1,77
Расчетным условие является: 468,1 МПа<570 МПа Контактная усталостная прочность обеспечена. Проверяем на усталостную изгибную прочность: Изгибная прочность зубьев шестерни и колеса в общем случае разная, поэтому для дальнейшего расчета необходимо установить «слабый» элемент. «Слабым», подлежащим дальнейшему проверочному расчету, зубчатым колесом пары будет то, у которого меньше отношение
Определяем допускаемое изгибное напряжение:
где σFlimb – предел выносливости зубьев при изгибе; SH – коэффициент запаса; KFC – коэффициент, учитывающий направление приложения нагрузки к зубьям; KFL – коэффициент долговечности. для шестерни: по таблице 39 стр. 109 [1] принимаем
Принимаем KFC=1, KFL =1, и по таблице 41 принимаем SH=2,2.
для колеса:
Принимаем KFC=1, KFL =1, SH=2,2.
Принимаем по таблице 24 стр. 78 [1] при Z1=40 и Z2=100 и более YF1=3,7 и YF2=3,6.
Более «слабым» элементом является колесо, по которому ведется дальнейший расчет.
Расчетным условие является: 24,5 МПа<205 МПа Изгибная усталостная прочность обеспечена. Проверяем на контактную прочность при действии максимальных нагрузок: Определяем максимальное контактное напряжение:
где Кпер – коэффициент перегрузки
Расчетным условие является:
680МПа<1512 МПа Контактная прочность при действии максимальных нагрузок обеспечена. Проверяем на изгибную прочность при действии максимальных нагрузок: Определяем максимальное изгибное напряжение:
Расчетным условие является: 51,7 МПа<688 МПа Изгибная прочность при действии максимальных нагрузок обеспечена. Результаты расчетов обеих передач заносим в таблицу. Таблица 3 - Результаты расчетов
Расчет валов Выбираем в качестве материала вала конструкционную сталь 35 по ГОСТ 1050-88 со следующими механическими характеристиками: бВ=520МПа, бт =280Мпа, τТ =170МПа, б-1 =250МПа, τ-1 =150Мпа Определяем диаметр выходного конца входного вала: Так как конструкция вала на данном этапе расчета не известна, то предварительно определяем минимальный диаметр из расчета только на кручение:
где [τ] – условное допускаемое напряжение при кручении, обычно принимается из расчета [τ]=15-30 МПа. Таким образом, получаем:
Полученное значение диаметра округляем до ближайшего стандартного значения по ГОСТ 6636-69, которое должно соответствовать посадочному диаметру зубчатой муфты. Принимаем dвых=160 мм. Определяем диаметр выходного конца п
|

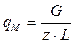 , кг/м
, кг/м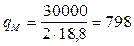 , кг/м
, кг/м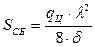 , кг
, кг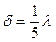 , м
, м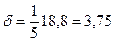 , м
, м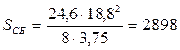 , кг
, кг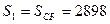 , кг
, кг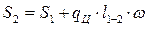 , кг
, кг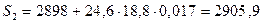 , кг
, кг , кг
, кг , кг
, кг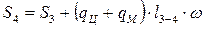 , кг
, кг , кг
, кг , кг
, кг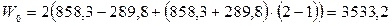 , кг
, кг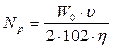 , кВт
, кВт , кВт
, кВт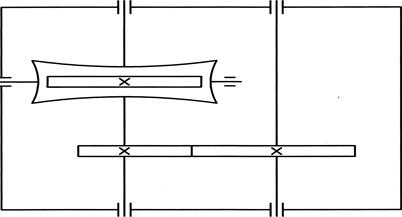
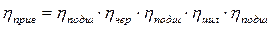
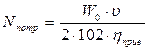
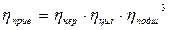
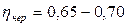
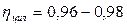

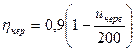
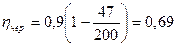
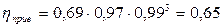
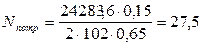 кВт
кВт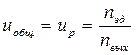
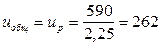
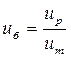
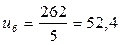
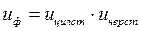
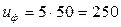

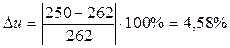
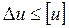 , можно сделать заключение о том, что кинематический расчет выполнен удовлетворительно.
, можно сделать заключение о том, что кинематический расчет выполнен удовлетворительно. об/мин
об/мин
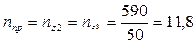 об/мин
об/мин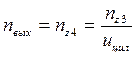
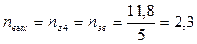 об/мин
об/мин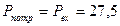 кВт
кВт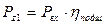
 кВт
кВт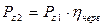
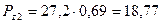 кВт
кВт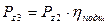
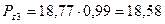 кВт
кВт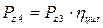
 кВт
кВт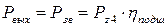
 кВт
кВт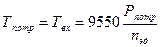
 Нм
Нм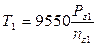
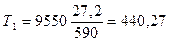 Нм
Нм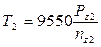
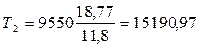 Нм
Нм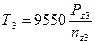
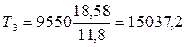 Нм
Нм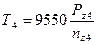
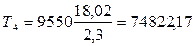 Нм
Нм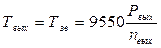
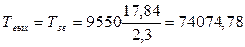 Нм
Нм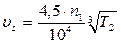
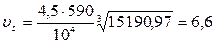 м/с
м/с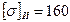 МПа
МПа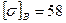 МПа
МПа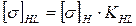
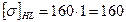 МПа
МПа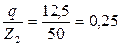
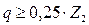
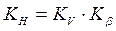
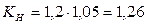
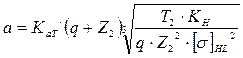
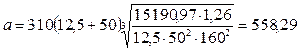 мм
мм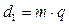
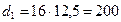 мм
мм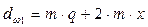
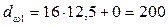 мм
мм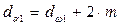
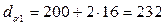 мм
мм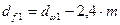
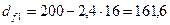 мм
мм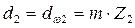
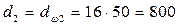 мм
мм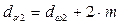
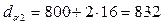 мм
мм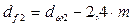
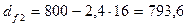 мм
мм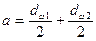
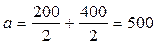 мм
мм
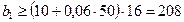 мм
мм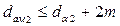
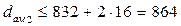 мм
мм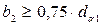
 мм.
мм.
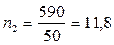 об/мин
об/мин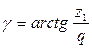
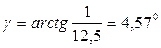
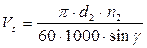
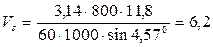 м/с
м/с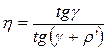

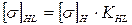
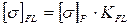
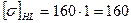 МПа
МПа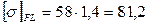 МПа
МПа
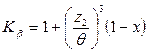

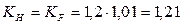


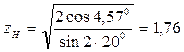
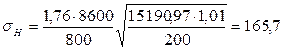 МПа
МПа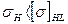
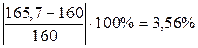
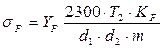

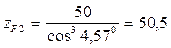
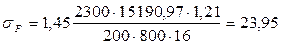
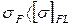
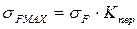
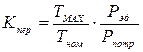
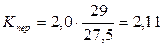
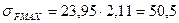 МПа
МПа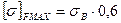
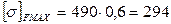 МПа
МПа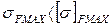
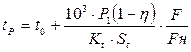
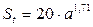
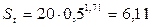 м2
м2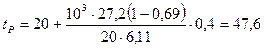 0С
0С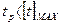

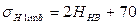
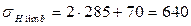 МПа
МПа МПа
МПа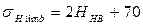
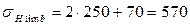 МПа
МПа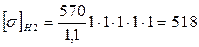 МПа
МПа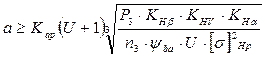
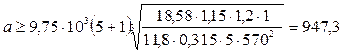 мм
мм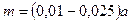
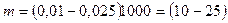 мм
мм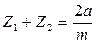
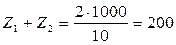 - целое число.
- целое число.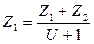
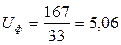
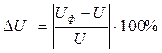
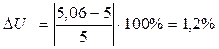
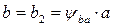
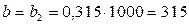 мм
мм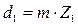
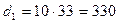 мм
мм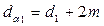
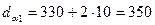 мм
мм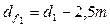
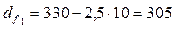 мм
мм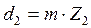
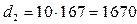 мм
мм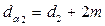
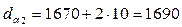 мм
мм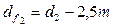
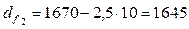 мм
мм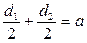
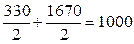 мм
мм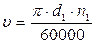
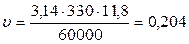 м/с
м/с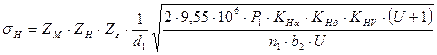 где ZM – коэффициент, учитывающий механические свойства материалов спряженных зубчатых колес, принимаем по таблице 21: «Значения ZM» стр. 72 [1] равным 275 МПа½;
где ZM – коэффициент, учитывающий механические свойства материалов спряженных зубчатых колес, принимаем по таблице 21: «Значения ZM» стр. 72 [1] равным 275 МПа½;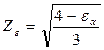
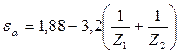
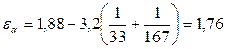
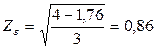
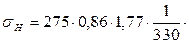
 МПа
МПа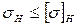
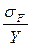

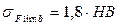
 МПа
МПа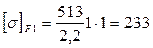 МПа
МПа
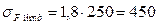 МПа
МПа МПа
МПа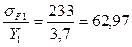
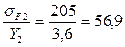
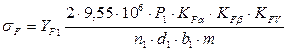
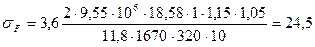

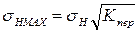
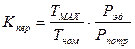
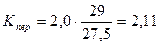
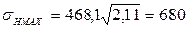 МПа
МПа
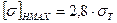
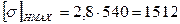 МПа
МПа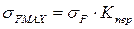
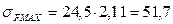 МПа
МПа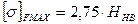
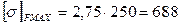 МПа
МПа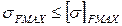
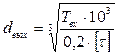
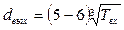
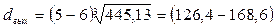 мм
мм


