Основные методы нахождения точечных оценок.
Основные методы нахождения точечных оценок. 1. Метод моментов (Гмурман. Руководство … §2, с. 163-164, пример. 471) состоит в приравнивании теоретических моментов данного распределения соответствующим эмпирическим моментам того же порядка. Он основывается на том факте, что эмпирическая функция распределения при большом числе наблюдений мало отличается от теоретической, поэтому выборочные моменты являются асимметрично несмещенными и состоятельными оценками теоретических моментов. В результате применения этого метода получают систему уравнений. При числе уравнений, большем 4, т.е. если параметров больше 4, этот метод не дает точной оценки. Если распределение характеризуется 1 параметром, то для его отыскания приравнивают 1 теоретический момент одному эмпирическому моменту того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка, т.е.
Если известна плотность распределения вероятности f (x) = f (x, M(X)) в случае непрерывного распределения или закон распределения pi = P(X= xi, M(X)), то уравнение (1) в развернутом виде можно записать так
Как видим, математическое ожидание является функцией от неизвестного параметра заданного распределения, поэтому, решив уравнение (1), получим его точечную оценку. Для случая двух параметров, приравнивая, например, начальные моменты первого порядка и центральные моменты второго порядка, имеем систему
Замечание. Метод моментов содержит неопределенность, поскольку можно получить уравнения для неизвестных параметров, приравняв как начальные, так и центральные моменты. Пример. СВ Х распределена по закону Пуассона
где m – число испытаний в одном опыте, xi – число появлений события в i -ом опыте. Найти методом моментов по выборке Решение. Для оценки одного параметра достаточно одного уравнения вида (1). Т.к. для распределения Пуассона M(X) = λ, то точечной оценкой этого параметра в силу уравнения (1) будет выборочная средняя, т.е.
2. Метод наибольшего правдоподобия (Гмурман. Руководство … §3, с. 169-171, пример. 493) используется в том случае, когда известен вид функции распределения. Он состоит в построении по этой функции так называемой функции правдоподобия и нахождении максимума этой функции (или ее логарифма). Пусть СВ Х в результате n испытаний приняла значения Определение 5. Функцией правдоподобия СВ Х называется функция
где Из определения следует, что функция правдоподобия является вероятностной мерой выборки Определение 6. Оценкой наибольшего правдоподобия параметра θ называется такое значение θ*, при котором функция правдоподобия достигает максимума. Определение 7. Логарифмической ф ункцией правдоподобия СВ Х называется функция ln L. Функции L и ln L достигают максимума при одном и том же значении θ, поэтом вместо отыскания максимума функции L ищут, что удобнее, максимум ln L. При отыскании точки максимума функции ln L аргумента θ поступают следующим образом. 1. Находят производную 2. Из уравнения правдоподобия, которое получается в результате приравнивания этой производной нулю, находят критическую θ*. 3. Находят вторую производную Пример. Найти методом наибольшего правдоподобия по выборке Решение. Учитывая, что θ = μ, составим функцию правдоподобия
Найдем логарифмическую функцию правдоподобия
Составим уравнение правдоподобия
из которого получаем критическую точку Найдем вторую производную
которая отрицательна, при любом μ, т.е. полученная оценка μ * является оценкой наибольшего правдоподобия неизвестного параметра μ. Замечание. Метод моментов отличается простотой, однако, оценки, полученные этим методом, как правило, смещены и малоэффективны. Исключение составляет нормальное распределение. Метод наибольшего правдоподобия дает состоятельную оценку; если существует эффективная оценка, то метод наибольшего правдоподобия дает ее; и оценка наибольшего правдоподобия асимптотически эффективна.
|

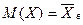 . (1)
. (1)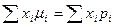 , если Х – дискретна,
, если Х – дискретна,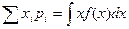 , если Х – непрерывна.
, если Х – непрерывна.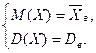
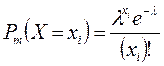 ,
,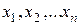 точечную оценку неизвестного параметра λ.
точечную оценку неизвестного параметра λ.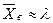 .
.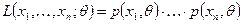 для дискретной СВ,
для дискретной СВ,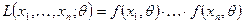 для непрерывной СВ,
для непрерывной СВ,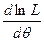 .
.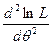 . Если она при θ = θ* отрицательна, то θ* - точка максимума функции ln L.
. Если она при θ = θ* отрицательна, то θ* - точка максимума функции ln L.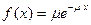 при неотрицательных x.
при неотрицательных x.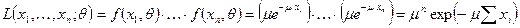 .
.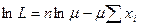 .
.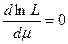 или
или  ,
,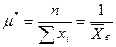 .
.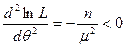 ,
,


