Влияние изменения частоты напряжения источники питания на механические характеристики асинхронной машины
Для изменения частоты напряжения, подводимого к обмотке статора асинхронной машины, применяются электромашинные и тиристорные преобразователи частоты. Как влияет частота напряжения источника питания на механические характеристики асинхронной машины? Известно, что угловая скорость вращения магнитного поля асинхронной машины пропорциональна частоте источника питания f1 ω=2πf1/p. В таком случае и скорость идеального холостого хода асинхронной машины, которой соответствует точка пересечения механической характеристики с осью ординат, пропорциональна частоте ω=ω1. Пропорционально частоте изменяются индуктивные сопротивления обмоток статора и ротора x=2πf1L. Пусть напряжение источника питания, подводимое к обмотке статора асинхронной машины, остается величиной постоянной, равной номинальному значению U1=U1НОМ. С целью уменьшения весогабаритных показателей асинхронные машины проектируются насыщенными. В этом случае в соответствии с выражением U1≈E1=4,44f1w1 Фm=const возможно только увеличение частоты, что вызывает соответствующее уменьшение магнитного потока. Так как угловая скорость и индуктивные сопротивления входят в знаменатель выражения для электромагнитного момента (56), то момент асинхронного двигателя с увеличением частоты будет уменьшаться. Увеличение индуктивных сопротивлений обмоток статора и ротора xK=x1+x2’ при увеличении частоты приводит к уменьшению токов в обмотках и уменьшению критического скольжения (52), (53), (57). Как влияет изменение частоты на энергетические показатели асинхронной машины? Коэффициент мощности заметно уменьшается с уменьшением частоты и возрастает при ее увеличении от номинального значения. На потери в стали с одной стороны влияет увеличение частоты, а с другой стороны уменьшение магнитного потока. Электрические потери в обмотке ротора растут пропорционально квадрату частоты, а потери в обмотке статора зависят от соотношения между токами I10 и I2’, из которых I10 уменьшается с возрастанием частоты, a I2’ возрастает. В целом потери в двигателе растут, но растет и полезная мощность PМЕХ=ωМ=2πnM. током сверх допустимой температуры даже при отсутствии полезной нагрузки на его валу. Поэтому в дальнейшем будет рассматриваться влияние на механические характеристики асинхронной машины только изменения напряжения от номинального значения до нуля. Итак, пусть напряжение U1, подаваемое на статорную обмотку асинхронного двигателя, уменьшается от номинального значения. Угловая скорость вращения магнитного поля не зависит от напряжения ω1=2πf/p, следовательно, все механические характеристики пройдут через одну точку на оси ординат, соответствующую режиму идеального холостого хода асинхронного двигателя (S=О). Момент, развиваемый двигателем при любом скольжении, пропорционален квадрату приложенного напряжения (56), а токи обмоток статора и ротора пропорциональны приложенному напряжению (52) и (53);
I1=U1[1/Zm+ 1/(Z1+Z /2S)].
u11>u12>u13 Рис.11. Механические характеристики асинхронного двигателя при изменении напряжения источника питания Из приведенного на рис.11 семейства механических характеристик асинхронной машины при изменении напряжения видно, что критическое скольжение для всех характеристик остается неизменным, независящим от приложенного напряжения (57)
Крутизна характеристик при понижении напряжения возрастает, но так как Sк остается неизменным, то регулирование скорости двигателя возможно лишь в узких пределах. схеме замещения при изменения скольжения S изменяются не только токи I1 и I /2, но и ток намагничивающего контура I10, а следовательно, изменяется и ЭДC машины, в то время как напряжение сети остается постоянным независящим от нагрузки и режима работы.
Рис.5. Г-образные схемы замещения асинхронной машины. на зажимы с напряжением сети U1. Для обоснования такой схемы замещения сделаем некоторые математические преобразования выражений, составленных по Т-образной схеме замещения асинхронной машины. При синхронном вращении ротора и поля, т.е. в режиме идеального холостого хода асинхронной машины имеем: S=0; r /2(1-S)/S = ∞; İ /2=0; İ1=İ10. Для намагничивающей ветви Т-образной схемы замещения можно записать -Ė1 = -Ė /2 = İ10 · Zm = İ10(rm+jxm) (34) Подставим значение ЭДС E1 в уравнение напряжения (33), записанное для цепи статора в режиме идеального холостого хода, U1 = -Ė1 + Z1İ10 = Zmİ10 + Z1İ10=[(r1+rm) + j(x1+xm)]İ10 (35) Найдем отношение напряжения сети U1 (35) к ЭДС E1 (34) для идеального холостого хода асинхронной машины (36) Комплексный коэффициент С1 может быть представлен в алгебраической, показательной и тригонометрической формах
(37)
(38) В асинхронных машинах малой и средней мощности коэффициент С1 близок к единице и равен С1≈1,02-1,08.
(39) Подставим это выражение для тока İ10 в уравнение токов (33). Из этого уравнения с учетом выражения (36) найдем ток обмотки статора I1
(40) где İ00 - ток обмотки статора при идеальном холостом ходе, когда скольжение S=0, этот ток равен
(41) İ //2 - преобразованный ток рабочей ветви Т-образной схемы замещения
(42) Выразим ток İ //2 через напряжение сети U1 и параметры асинхронной машины. Для этого в системе уравнений (33) в уравнение напряжения, записанное для обмотки статора, подставим выражение ЭДС Е1, составленное для обмотки ротора, получим уравнение для напряжения U1 в виде U1=-Ė1+Z1İ1=-Z /2Sİ /2 + Z1İ1= - İ /2(r /2 + r /2 (1-S)/S + jx /2) + İ1(r1+jx1). Преобразуем полученное уравнение с учетом выражений (40)-(42) U1=-İ /2Z2S + İ1Z1 = -İ //2Ċ1Z /2S + (İ00 – İ //2)Z1 = İ00Z1 – İ //2(Ċ1Z /2S+Z1) = Из этого выражения найдем ток I2’’
3. ИССЛЕДОВАНИЕ МЕХАНИЧЕСКОЙ ХАРАКТЕРИСТИКИ АСИНХРОННОЙ МАШИНЫ Электрическая машина проектируется и изготавливается для определенного расчетного режима, называемого номинальным режимом работы. Этот режим реализуется в естественной схеме включения асинхронной машины при отсутствии добавочных сопротивлений в цепях статора и ротора и при номинальных значениях напряжения U1НОМ и частоты f1НОМ. Механическая статическая характеристика асинхронного двигателя, соответствующая этим условиям, называется естественной характеристикой. Процессы управления и регулирования электроприводов сводятся к изменению характеристик двигателя путем изменения схем соединения обмоток, введения в цепи статора и ротора добавочных сопротивлении, изменения напряжения и частоты источника питания. Механические характеристики, получаемые в этих случаях, называются искусственными характеристиками асинхронного двигателя.
|








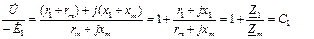

 В ряде случаев более удобной является другая, так называемая, Г-образная схема замещения асинхронной машины рис.5. в которой намагничивающая ветвь вынесена
В ряде случаев более удобной является другая, так называемая, Г-образная схема замещения асинхронной машины рис.5. в которой намагничивающая ветвь вынесена



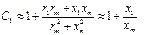 Мнимая часть комплексного числа С1 обычно отрицательная, в связи с чем аргумент γ имеет знак минус. Аргумент γ определяет угол поворота вектора ЭДC (-Е1) относительно напряжения U. В связи с тем, что угол γ мал, например, в машинах, мощностью более 8 кВт угол γ<1°, то с достаточной степенью точности коэффициент С1 может быть определен как вещественное число
Мнимая часть комплексного числа С1 обычно отрицательная, в связи с чем аргумент γ имеет знак минус. Аргумент γ определяет угол поворота вектора ЭДC (-Е1) относительно напряжения U. В связи с тем, что угол γ мал, например, в машинах, мощностью более 8 кВт угол γ<1°, то с достаточной степенью точности коэффициент С1 может быть определен как вещественное число Из Т-образной схемы замещения найдем ток намагничивающей ветви I10
Из Т-образной схемы замещения найдем ток намагничивающей ветви I10


 -İ //2(Ċ1Z2S’+Z1);
-İ //2(Ċ1Z2S’+Z1);



