Трехфазная асинхронная машина при вращающемся роторе
В асинхронной машине, как и в трансформаторе, имеет место магнитная связь между первичной обмоткой, расположенной на статоре и вторичной обмоткой, расположенной на роторе. Однако, в отличие от трансформатора вторичная обмотка асинхронной машины вращается с угловой скоростью ω и ее проводники перемещаются в магнитном поле, которое в свою очередь вращается с угловой скоростью ω1. Следовательно, частота ЭДС, тока, величины индуктивных сопротивлений обмотки ротора являются функциями скольжения S.
где ω1 - угловая скорость вращения поля; ω2 - угловая скорость вращения ротора. Как и при неподвижном роторе, МДС обмотки F2 при вращении ротора асинхронной машины вращается с той же угловой скоростью ω1 относительно статора, что и МДС обмотки статора F1. Докажем это. Пусть асинхронная машина работает в режиме двигателя, и под действием электромагнитного момента ротор вращается с угловой скоростью ω в сторону вращения магнитного поля. В этом случае угловая скорость вращения магнитного поля, созданного током обмотки статора относительно проводников обмотки ротора уменьшается и станет равной ω2=ω1-ω=2πf2/p, (14) Из этой формулы найдем выражение для частоты f2 Таким образом, частота ЭДC и тока в обмотке ротора пропорциональна скольжению S. Действующее значение ЭДС вращающегося ротора равно E2S=4,44f2w2kоб2Фm=4,44f1Sw2kоб2Фm=SE2, (15) где E2 - ЭДC неподвижного ротора (12). Протекая по обмотке ротора, ток I2 создает МДС F2 и магнитный поток Ф2, вращающиеся относительно ротора с угловой скоростью ω2, соответствующей частоте тока в роторе f2. Но в свою очередь ротор вращается относительно неподвижного статора с угловой скоростью ω. Таким образом, результирующая угловая скорость вращения МДC F2 и магнитного потока Ф2 относительно статора определяется как сумма угловых скоростей (ω+ω2)=ω+ω1-ω=ω1. Следовательно, МДС F2 и магнитный поток Ф2 обмотки ротора вращаются относительно статора с той же самой угловой скоростью, что и МДС F1 и магнитный поток Ф1, созданные токами обмотки статора. МДС F1 и F2 сдвинуты в пространстве относительно друг друга на такой угол, чтобы получить результирующую синусоидальную волну MДC F10, необходимую для создания основного магнитного потока Ф. По аналогии с трансформатором получаем
Из полученного уравнения найдем ток I10
где I /2=1/кi · I2 - ток ротора, приведенный к обмотке статора;
Из уравнения (18) найдем ток обмотки статора асинхронной машины
1.4. Приведение рабочего процесса асинхронной машины при вращающемся роторе к рабочему процессу при неподвижном роторе Как уже отмечалось в параграфе 1.2. при неподвижном роторе асинхронная машина работает в качестве трансформатора, при этом электрическая энергия из первичной цепи посредством магнитного поля передается во вторичную цепь. Электрическая энергия во вторичной цепи неподвижной асинхронной машины преобразуется в тепловую и нагревает машину. Во вращающейся асинхронной машине, работающей, например, в двигательном режиме, электрическая энергия, потребляемая обмоткой статора из сети, во вторичной цепи превращается в механическую энергию на валу машины и частично, в тепловую энергию, выделяемую на сопротивлениях обмотки ротора. Исследование режимов работы вращающейся асинхронной машины более сложная задача, чем исследование режимов работы трансформатора, так как частоты ЭДС и токов обмоток статора и ротора не равны. По этой причине невозможно непосредственное изображение электрических величин, относящихся к статору и ротору на одной плоскости, так как они будут вращаться с разными угловыми скоростями, пропорциональными соответствующим частотам. одновременно с этим уменьшаются частота тока и индуктивное сопротивление реактора. Все это приводит к тому, что ток ротора будет спадать, не так быстро, как при наличии только активного сопротивления. Поскольку момент асинхронного двигателя (M=CMФmI2cosψ2) пропорционален магнитному потоку Фm,(который в процессе пуска в первом приближении можно принять постоянным), уменьшающемуся току ротора I2 и возрастающему коэффициенту мощности обмотки ротора, то при ускорении двигателя момент будет почти постоянен и вначале может даже несколько возрастать.
(68)
(69) Тогда формула для расчета искусственной механической характеристики примет вид (с учетом
(70) Приведенный ток ротора определяется по выражению (52)
(71)
|

 , (13)
, (13) (16) Подставим в это уравнение значения МДC по формулам (6) и (9).
(16) Подставим в это уравнение значения МДC по формулам (6) и (9). , (17)
, (17)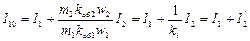 , (18)
, (18)
 - коэффициент приведения токов. (19)
- коэффициент приведения токов. (19) , (20) Таким образом, как и в трансформаторе, ток обмотки статора асинхронной машины состоит из двух составляющих: намагничивающего тока İ10, который обусловливает создание вращающегося магнитного поля в зазоре машины, и тока (-İ /2), который компенсирует размагничивающее действие со стороны обмотки ротора.
, (20) Таким образом, как и в трансформаторе, ток обмотки статора асинхронной машины состоит из двух составляющих: намагничивающего тока İ10, который обусловливает создание вращающегося магнитного поля в зазоре машины, и тока (-İ /2), который компенсирует размагничивающее действие со стороны обмотки ротора. Критическое скольжение и критический момент для искусственной механической характеристики могут быть найдены по формулам:
Критическое скольжение и критический момент для искусственной механической характеристики могут быть найдены по формулам: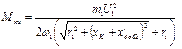
 63)
63)



