Примеры расчетов. Пример 13. Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.26,а)
Пример 13. Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.26,а), методом Мора. Рассмотрим три состояния балки: первое (грузовое) – при действии заданной распределенной нагрузки q; ему соответствует эпюра моментов (рис.26,в). Третье состояние (также единичное) – при действии сосредоточенного момента
Вычисляем прогиб балки в точке С:
Знак "+" означает, что точка С переместится в направлении действия силы. Вычисляем угол поворота сечения В:
Рис. 26
Рис. 27 Знак "+" означает, что сечение В поворачивается в направлении действия момента Пример 14. Определить прогиб балки в середине пролета (рис.27,а) методом Мора. Оценить влияние поперечной силы на общую величину прогиба. Рассмотрим два состояния балки. Первое состояние (грузовое) – при действии силы F (рис.27,а); ему соответствует эпюры изгибающих моментов Второе состояние (единичное) – при действии силы В связи с отсутствием продольных сил в поперечных сечениях балки интеграл Мора (2.18) принимает вид:
Подставляя значения изгибающих моментов и поперечных сил в сечении с координатой z (рис.27) для составляющих полного перемещения получим:
Оценим влияние поперечной силы на общую величину прогиба. Пусть рассматриваемая балка имеет прямоугольное поперечное сечение со сторонами b и h, при этом h=0,1ℓ. Тогда площадь сечения и его осевой момент инерции равны:
Будем считать, что
то есть прогиб, обусловленный деформацией сдвига, составляет 3% от прогиба, обусловленного изгибом. Легко убедиться, что при увеличении отношения
|

 (рис.26,б). Второе состояние (единичное) – при действии сосредоточенной силы
(рис.26,б). Второе состояние (единичное) – при действии сосредоточенной силы  , приложенной в точке С; ему соответствует эпюра моментов
, приложенной в точке С; ему соответствует эпюра моментов 
 , приложенного в точке В; ему соответствует эпюра моментов
, приложенного в точке В; ему соответствует эпюра моментов  (рис.26,г). Примем начало координат на левой опоре; тогда ординаты указанных эпюр в сечении с координатой z соответственно равны:
(рис.26,г). Примем начало координат на левой опоре; тогда ординаты указанных эпюр в сечении с координатой z соответственно равны:
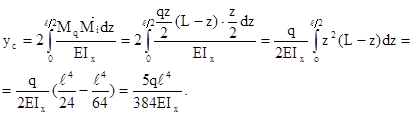




 то есть по часовой стрелке.
то есть по часовой стрелке. (рис.27,б) и поперечных сил
(рис.27,б) и поперечных сил  (рис.27,в).
(рис.27,в). (рис.27,г); ему соответствуют эпюры изгибающих моментов
(рис.27,г); ему соответствуют эпюры изгибающих моментов  (рис.27,е).
(рис.27,е).




 тогда:
тогда:
 влияние поперечных сил на величину прогиба становится еще менее значительным.
влияние поперечных сил на величину прогиба становится еще менее значительным.


