Работа внешних сил. Потенциальная энергия
Определим работу силы F, статически приложенной к некоторой упругой системе (рис.20, а), материал которой следует закону Гука.
Рис. 20 При малых деформациях к этой системе применим принцип независимости действия сил, следовательно, перемещения отдельных точек и сечений конструкции прямо пропорциональны вызывающей их нагрузке:
где Составим выражение элементарной работы внешней силы на перемещении Заменим
Интегрируя это выражение в пределах полного изменения силы от нуля до ее конечного значения, получим формулу для определения работы, совершаемой статически приложенной внешней силой F:
или, с учетом(2.2):
то есть работа внешней силы при статическом действии ее на любое упругое сооружение равна половине произведения значения этой силы на величину соответствующего ей перемещения. Для обобщения полученного вывода под силой понимают любое воздействие, приложенное к упругой системе, то есть не только сосредоточенную силу, но и момент или равномерно распределенную нагрузку; под перемещением понимают тот его вид, на котором данная сила производит работу: сосредоточенной силе соответствует линейное перемещение, сосредоточенному моменту – угловое, равномерно распределенной нагрузке – площадь эпюры перемещений на участке действия нагрузки. При статическим действии на конструкцию группы внешних сил работа этих сил равна половине суммы произведений каждой силы на величину соответствующего ей перемещения, вызванного действием всей группы сил. Например, при действии на балку (рис.20,б) сосредоточенных сил F1, F2 и сосредоточенных моментов М1 и М2 работа внешних сил:
Работу внешних сил на вызванных ими перемещения можно выразить и иначе – через внутренние силовые факторы (изгибающие моменты, продольные и поперечные силы), возникающие в поперечных сечениях системы. Выделим из прямолинейного стержня двумя сечениями, перпендикулярными его оси (рис.21, а), бесконечно малый элемент dz. Стержень состоит из бесконечно большого числа таких элементов. К каждому элементу dz в общем случае плоской задачи приложены продольная сила Nz, изгибающий момент Мх и поперечная сила Qy. Для выделенного элемента dz усилия N, M, Q являются внешними силами, поэтому работу Рассмотрим элемент dz, находящийся только под действием продольных сил N (рис.21,б). Если его левое сечение считать неподвижным, то правое сечение под влиянием продольной силы переместится вправо на величину
Рис. 21 Если неподвижно закрепить левое сечение элемента dz, находящегося под действием только изгибающих моментов М (рис.22,а), то взаимный угол поворота торцевых сечений элемента будет равен углу поворота
На этом перемещении момент М совершит работу:
Рис. 22 Закрепим левое сечение элемента dz, находящегося под действием только поперечных сил Q (рис.22,б,в), а к правому приложим касательные усилия
а работа силы Q на этом перемещении будет:
В действительности касательные напряжения Суммируя (2.5) – (2.7), получим полное значение работы:
Интегрируя выражение
Из формулы (2.9) следует, что работа внешних сил на вызванных ими перемещениях всегда положительна. На основании закона сохранения энергии работа
|


 , (2.2)
, (2.2) - перемещение по направлению силы F;
- перемещение по направлению силы F;  - некоторый коэффициент, зависящий от материала, схемы и размеров сооружения. Увеличение силы F на бесконечно малую величину dF вызовет увеличение перемещения на
- некоторый коэффициент, зависящий от материала, схемы и размеров сооружения. Увеличение силы F на бесконечно малую величину dF вызовет увеличение перемещения на  .
. .
. .
.
 , (2.3)
, (2.3)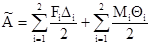 (2.4)
(2.4) можно получить как сумму работ, совершенных статически возрастающими усилиями N, M, Q на соответствующих деформациях элементов dz.
можно получить как сумму работ, совершенных статически возрастающими усилиями N, M, Q на соответствующих деформациях элементов dz. . На этом перемещении сила N совершит работу:
. На этом перемещении сила N совершит работу: (2.5)
(2.5)
 его правого сечения:
его правого сечения: .
. (2.6)
(2.6)
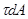 , равнодействующей которых является поперечная сила Q. Предположим, что касательные напряжения
, равнодействующей которых является поперечная сила Q. Предположим, что касательные напряжения  равномерно распределены по всей площади А поперечного сечения, то есть
равномерно распределены по всей площади А поперечного сечения, то есть  , тогда перемещение
, тогда перемещение  определяется в виде:
определяется в виде: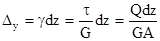 ,
, (2.7)
(2.7) .
. (2.8)
(2.8)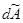 в пределах длины L каждого участка всех стержней и суммируя результаты, получим:
в пределах длины L каждого участка всех стержней и суммируя результаты, получим: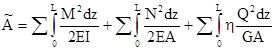 (2.9)
(2.9) .
.


