Теорема о взаимности работ
Рассмотрим два состояния упругой системы, находящейся в равновесии. В каждом из этих состояний на систему действует некоторая статическая нагрузка (рис.23,а). Обозначим перемещения по направлениям сил F1 и F2 через
Рис. 23 Обозначим работу нагрузки первого состояния (сила F1) на перемещениях первого состояния через А11, а работу силы F2 на вызванных ею перемещениях – А22:
Используя (2.9), работы А11 и А22 можно выразить через внутренние силовые факторы:
Рассмотрим случай статического нагружения той же системы (рис.23,а) в такой последовательности. Сначала к системе прикладывается статически возрастающая сила F1 (рис.23,б); когда процесс ее статического нарастания закончен, деформация системы и действующие в ней внутренние усилия становятся такими же, как и первом состоянии (рис.23,а). Работа силы F1 составит:
Затем на систему начинает действовать статически нарастающая сила F2 (рис.23,б). В результате этого система получает дополнительные деформации и в ней возникают дополнительные внутренние усилия, такие же, как и во втором состоянии (рис.23,а). В процессе нарастания силы F2 от нуля до ее конечного значения сила F1, оставаясь неизменной, перемещается вниз на величину дополнительного прогиба
Сила F2 при этом совершает работу:
Полная работа А при последовательном нагружении системы силами F1, F2 равна:
С другой стороны, в соответствии с (2.4) полную работу можно определить в виде:
Приравнивая друг к другу выражения (2.11) и (2.12), получим:
или А12=А21 (2.14) Равенство (2.14) носит название теоремы о взаимности работ, или теоремы Бетти: работа сил первого состояния на перемещениях по их направлениям, вызванных силами второго состояния, равна работе сил второго состояния на перемещениях по их направлениям, вызванных силами первого состояния. Опуская промежуточные выкладки, выразим работу А12 через изгибающие моменты, продольные и поперечные силы, возникающие в первом и втором состояниях:
Каждое подинтегральное выражение в правой части этого равенства можно рассматривать как произведение внутреннего усилия, возникающего в сечении стержня от сил первого состояния, на деформацию элемента dz, вызванную силами второго состояния.
|

 , где индекс “i” показывает направление перемещения, а индекс “j” – вызвавшую его причину.
, где индекс “i” показывает направление перемещения, а индекс “j” – вызвавшую его причину.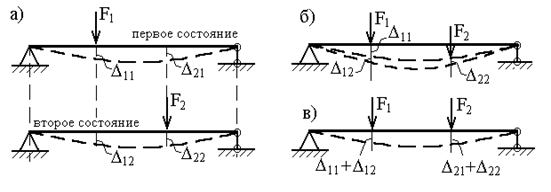
 .
. (2.10)
(2.10)
 и, следовательно, совершает дополнительную работу:
и, следовательно, совершает дополнительную работу:

 (2.11)
(2.11) (2.12)
(2.12) (2.13)
(2.13) (2.15)
(2.15)


