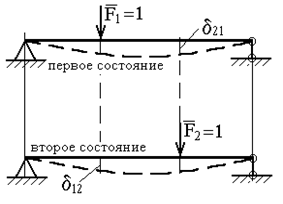
Теорема о взаимности перемещений
Пусть в первом состоянии к системе приложена сила На основании теоремы о взаимности работ:
Рис. 24 Полученное равенство (2.16) носит название теоремы о взаимности перемещений (или теоремы Максвелла): для двух единичных состояний упругой системы перемещение по направлению первой единичной силы, вызванное второй единичной силой, равно перемещению по направлению второй силы, вызванному первой силой.
|
, а во втором - 
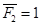(рис.24). Обозначим перемещения, вызванные единичными силами (или единичными моментами 
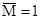) символом 
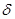. Тогда перемещение рассматриваемой системы по направлению единичной силы 
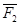в первом состоянии (то есть вызванное силой 
) - 
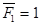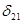, а перемещение по направлению силы 
.
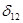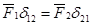, но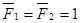 
, поэтому 
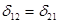, или в общем случае действия любых единичных сил:
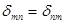(2.16)
