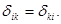Канонические уравнения метода сил
Для получения дополнительных уравнений, о которых говорилось в предыдущем параграфе, нужно прежде всего превратить заданную, n раз статически неопределимую систему, в статически определимую, удалив из нее лишние связи. Полученная статически определимая система называется основной. Отметим, что преобразование заданной системы в статически определимую не является обязательным. Иногда используется модификация метода сил, в которой основная система может быть статически неопределимой, однако изложение этого вопроса выходит за рамки этого пособия. Устранение каких-либо связей не изменяет внутренние усилия и деформации системы, если к ней приложить дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Значит, если к основной системе приложить заданную нагрузку и реакции удаленных связей, то основная и заданная системы станут эквивалентными. В заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе, перемещений быть не может, поэтому и в основной системе перемещения по направлениям отброшенных связей должны равняться нулю. А для этого реакции отброшенных связей должны иметь строго определенные значения. Условие равенства нулю перемещения по направлению любой i-ой связи из n отброшенных на основании принципа независимости действия сил имеет вид:
где первый индекс означает направление перемещения и номер отброшенной связи, а второй указывает на причину, вызвавшую перемещение, т.е. В методе сил реакцию k-ой связи принято обозначать через Xk. С учетом этого обозначения и в силу справедливости закона Гука перемещения
где Подставляя (3.2) в (3.1), получим:
Физический смысл уравнения (3.3): перемещение в основной системе по направлению i-ой отброшенной связи равно нулю. Записывая выражения, аналогичные (3.3), для всей совокупности отброшенных связей, получим систему канонических уравнений метода сил:
Вид уравнения (3.4), т.е. количество слагаемых в каждом из них и их общее число, определяется только степенью статической неопределимости системы и не зависит от ее конкретных особенностей. Коэффициенты системы канонических уравнений (3.4) определяются методом Мора-Верещагина путем перемножения соответствующих эпюр. Все эти коэффициенты, как указывалось выше, представляют собой перемещения; коэффициенты, стоящие при неизвестных – единичные перемещения, а свободные члены – грузовые. Единичные перемещения делятся на главные, расположенные по главной диагонали и имеющие одинаковые индексы (
|

 (3.1)
(3.1) - это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи;
- это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи; 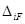 - перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки.
- перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки. (3.2)
(3.2) - единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией
- единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией 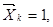 т.е. реакцией, совпадающей по направлению с Xk, но равной единице.
т.е. реакцией, совпадающей по направлению с Xk, но равной единице. (3.3)
(3.3) (3.4)
(3.4) ), и побочные (
), и побочные (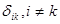 ). Главные перемещения всегда положительные, в отличие от побочных. Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е.
). Главные перемещения всегда положительные, в отличие от побочных. Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е.