Вероятность α отвергнуть гипотезу, когда она верна, называется уровнем значимости критерия.
Одной из важных задач статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по опытным данным. Предположение о виде распределения может быть сделано, исходя из теоретических предпосылок (выполнение условий центральной предельной теоремы может свидетельствовать о нормальном законе распределения случайной величины), опыта аналогичных предшествующих исследований, на основании графического изображения эмпирического распределения. Параметры распределения, как правило, неизвестны, их заменяют наилучшими оценками по выборке. Между эмпирическим и теоретическим распределениями неизбежны расхождения. Возникает вопрос: эти расхождения объясняются случайными обстоятельствами или они являются существенными и теоретический закон распределения подобран неудачно. Для ответа на этот вопрос служат критерии согласия.
Одним из наиболее мощных критериев согласия является критерий Пирсона, называемый еще критерием Хи-квадрат. Его суть заключается всравнении эмпирических частот элементов выборки ni(для дискретных распределений) с теоретическими частотами ni ′ = npi, где pi - вероятность принять это значение, рассчитанное по исследуемому закону распределения. Если распределение непрерывное, то строитсягруппированный статистический ряд из k интервалови pi = F (bi) - F (ai ) есть вероятность попасть в i -й интервал группировки (здесь F (x) - функция распределения проверяемого закона функция Лапласа). Статистикой критерия являетсявеличина
Если
ПРИМЕР 1. Имеется выборка измерения пульса у 40 больных, подвергнутых некоторой лечебной процедуре. Проверить гипотезу о том, что значение пульса у подобных больных распределенопо нормальномузакону распределения. Взять уровень значимости α= 0,05.
Выборка ЧСС у 40больных (уд/мин).
|

 . Эта величина является мерой расхождения эмпирических частот ni и теоретических частот ni ′.Критическое значение критерия равно обратному распределению хи-квадрат со степенями свободы
. Эта величина является мерой расхождения эмпирических частот ni и теоретических частот ni ′.Критическое значение критерия равно обратному распределению хи-квадрат со степенями свободы 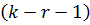 :
: ,гдеk–количество интервалов эмпирического распределения, r – число оцениваемыхпараметров закона распределения, α; –заданный уровень значимости.
,гдеk–количество интервалов эмпирического распределения, r – число оцениваемыхпараметров закона распределения, α; –заданный уровень значимости.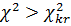 , то гипотеза H0 отвергается; есливыполняется условие
, то гипотеза H0 отвергается; есливыполняется условие  , то распределение можно считать соответствующим теоретическому, другими словами гипотеза H0не противоречит опытным данным.
, то распределение можно считать соответствующим теоретическому, другими словами гипотеза H0не противоречит опытным данным.


