Молекулярно-массовое распределение при радикальной полимеризации
Нахождение дифференциальной функции числового распределения при радикальной полимеризации сводится к нахождению вероятности образования макромолекул с заданной степенью полимеризации р. Рассмотрим вначале полимеризацию, в которой обрыв цепи осуществляется путем диспропорционирования радикалов. В этом случае число частиц в результате реакции обрыва не изменяется:
где Р•m и Р•m - макрорадикалы; Рm и Рn - макромолекулы со степенью полимеризации m и n. Вероятность образования макромолекул со степенью полимеризации р может быть выражена следующим образом:
где ε - вероятность прекращения, а (1-ε) - вероятность продолжения роста цепи, А - коэффициент пропорциональности. Параметр ε описывается простым соотношением:
где Vo, Vp - скорости обрыва и роста цепи. Для дальнейшего важно ε << 1. При этом условии (
Значение A определяется из условия нормировки. Поскольку
то А = 1. Переходя к непрерывному распределению, окончательно имеем:
Ранее в подразд. 1.3.1 было показано, что существует количественная связь между дифференциальными числовой и массовой функциями распределения. Используя (1.7), получаем для дифференциальной массовой функции распределения:
Функции (5.38) и (5.39) описывают ММР полимера, полученного в условиях радикальной полимеризации при обрыве путем диспропорционирования и передачи цепи, а также полимера, полученного путем ступенчатой полимеризации (поликонденсации). Распределение, описываемое уравнением (5.38), называется нормальным распределением, наиболее вероятным распределением, а также распределением Флори. При таком распределении параметр полидисперсности Обрыв через рекомбинацию радикалов. Вэтом случае из двух макрорадикалов образуется одна макромолекула:
Макромолекулы со степенью полимеризации р могут быть получены в результате соединения радикалов, имеющих степень полимеризации р' и (р – р'), где 1<р'<(р-1). Тогда:
Поскольку A'=1 (см. выше), а все значения р' равновероятны, то
Распределение, отвечающее уравнению (5.41), называется уравнением Шульца. Переходя, аналогично предыдущему, к массовой функции распределения, получаем:
Параметр полидисперсности в данном случае равен
Видно, что форма кривых принципиально отлична, особенно в области малых p.
|




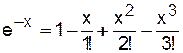 …, что при x<<1 дает e-x=1-x) уравнение (5.34) можно записать в виде:
…, что при x<<1 дает e-x=1-x) уравнение (5.34) можно записать в виде:



 w/
w/ 







