Построение исходной геодезической основы на исходном монтажном горизонте (на уровне «0» отметки).
Два этапа:
2. Измерения выполняются внутри между этими точками: точность 5 мм + точность за температуру. Для определения невязки делаем избыточное измерение. По двум Δ считаем координаты вычисленной стороны, находим диагональ и сравниваем ее с измеренной (для сведения к линейной форме составления уравнений).
Площадная форма условного уравнения:
После алгебраических преобразований: где
Для Гаусса (1864 г): А. К. Зайцев:
Формулы Буткевича:
Если привести подобные члены, получим следующий вид:
Заменяем поправки ошибками вычисленными допустимыми значениями невязки:
Так как измерения равноточные, то формула будет иметь вид:
Контрольная формула для вычисления коэффициентов А, В, С в каждом треугольнике: Aa – Bb – Cc = 0.
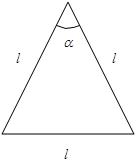
Точность вычисления угла α по теореме косинусов найдем из дифференцирования и после преобразования дифференциального уравнения получим формулу: В треугольниках типичной формы (прямоугольных, равнобедренных, равносторонних) все приведенные выше формулы упрощаются ввиду того что коэффициенты А, В, С становятся либо равными нулю, либо связаны с измеренной стороной.
1)
2)
Созданная на исходном монтажном горизонте сеть повторяется на каждом следующем монтажном горизонте, после переноса точек с исходного горизонта на этот горизонт. После этого рассчитывают разворот сети и смещение ее центра тяжести относительно сети на исходный монтажный горизонт. Если эти величины значимы (превышают ошибки измерения), необходимо в координаты точек на данном монтажном горизонте ввести соответствующие элементы редукции.
f, d, l – средние значения из двух соответствующих измерений, округленные до 0,001.
Невязку округляем до 1-х доле секунды. Измерения считаем равноточными (см. практические занятия).
Центр тяжести вычисляется как среднее арифметическое из четырех координат. Затем вычисляем уклонения координат фигуры от координат центра тяжести:
Формула для разворота исходного дирекционного угла:
Элементы редукции:
Среднее смещение вычисляется как среднее арифметическое из суммы элементов редукции.
Оценка точности:
[1] См. Неумывакин Ю. К., Перский М. И. Геодезическое обеспечение землеустроительных и кадастровых работ. – М., Картгеоцентр-Геодезиздат, 1996 г.
|

 Перенос точек сети со знаков закрепления осей на исходный монтажный горизонт. На рисунке – сеть микротрилатерации.
Перенос точек сети со знаков закрепления осей на исходный монтажный горизонт. На рисунке – сеть микротрилатерации. .
. из треугольника 124 – угловая форма.
из треугольника 124 – угловая форма. - поправки в вычисленные углы.
- поправки в вычисленные углы. ,
, - коэффициенты, определяемые следующим образом:
- коэффициенты, определяемые следующим образом: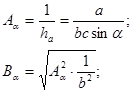
 .
.

 Условное уравнение:
Условное уравнение:  .
.

 .
.

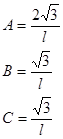



 .
.
 - сумма коэффициентов условных уравнений.
- сумма коэффициентов условных уравнений. ;
; 
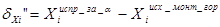 , для Y аналогично.
, для Y аналогично.
 - среднее значение погрешностей, n – число измеренных сторон.
- среднее значение погрешностей, n – число измеренных сторон.


