Основы гидродинамического подобия и метод анализа размерностей.
(Математическое и физическое моделирование)
нр Математическое моделирование. При исследовании гидравлических процессов с помощью математического моделирования изучаются явления, отличные от натурных (физических), но описываемые теми же математическими уравнениями. Совокупность уравнений, описывающих определённый физический процесс, называют математической моделью, а изучение его поведения в тех или иных условиях путём решения уравнений - математическим моделированием. Математическая модель гидравлического явления или процесса обычно создаётся на основании применения к ним наиболее общих законов механики, таких, как сохранение движения, массы и энергии. Записывая эти законы в виде систем дифференциальных уравнений и аналитически их исследуя, то есть используя методы классической механики, можно получить информацию о процессах или явлениях, которые не наблюдались в ограниченном диапазоне изменения исследуемых величин. Применяя общие теоремы механики или термодинамики к частным случаям потока жидкости в конкретных условиях, получают математические модели гидравлических процессов, как правило, в виде сложных систем дифференциальных уравнений в частных производных. Аналитические методы интегрирования и исследования таких уравнений, традиционные для классической механики и гидравлики, в настоящее время всё чаще вытесняются методами численного расчёта подобных систем с использованием ЭВМ. Другой путь состоит в том, что аналитические приёмы интегрирования и исследования систем дифференциальных уравнений используются в сочетании с эмпирическими приёмами. В этом случае зависимости, выведенные из фундаментальных законов механики, применяются при аналитическом исследовании совместно с зависимостями, установленными экспериментальным путём, обычно на основе осреднения данных натуральных изменений. Классическими примерами являются полуэмпирические теории турбулентности и теории пограничного слоя. Численный, или вычислительный, эксперимент - это современный метод теоретических исследований. опирающихся на “экспериментирование” с математической моделью, только роль лабораторной установки выполняет ЭВМ, ведущая вычисления по заданной программе. В настоящее время широко е развитие получили численные методы, ориентированные на использование современных быстродействующих ЭВМ. Среди них можно выделить 2 альтернативных метода численной, или вычислительной, гидравлики3 /26/, быстро развивающиеся в настоящее время, - метод конечного элемента (МКЭ) и метод конечных разностей (МКР). Применение этих методов заставило обратить внимание на целый ряд новых аспектов при исследовании гидравлических процессов. Особенно важным достижением в этой области следует считать исследования, связанные с изучением граничных условий при различных типах давления жидкости. Следует считать, что все последующие, значительные, достижения в гидравлике должны базироваться на рациональном использовании в одном исследовании всех 3 методов: аналитического, эмпирического и вычислительного. примерами математического моделирования являются: исследование движения грунтовых вод методом гидродинамических аналогий (ЭГДА), Физическое моделирование. При таком моделировании изучаемые гидравлические процессы воспроизводятся на модели, отличающейся в масштабе от натуры, на основе оьщих законов подобия механических систем. Явления (процессы) будут механически подобны в том случае, если в них одинаково отношение всех геометрических элементов - размеров, расстояний, перемещений, одинаково отношение плотностей и сил, действующих в соответственных точках и направлениях. Моделью в этом случае называется уменьшенное гидротехническое сооружение или гидравлическая машина вместе с омывающим её потоком жидкости.
Для полного гидродинамического подобия потоков необходимо их геометрическое, кинематическое и динамическое подобие. Два потока будут геометрически подобными, если между их соответствующими линейными размерами существует постоянное соотношение lH l M = a = const где а - линейный масштаб, показывающий во сколько раз размеры модели lM уменьшены, по сравнению с размерами натуры lH. Отметим, что в геометрически подобной модели русла все размеры, в том числе и высота выступов шероховатости Должны быть также постоянными соотношения площадей
Два потока будут подобны (к инематическим ) при подобии полей скоростей и ускорений натуры и модели, которое выполняется если скорости VH и V M и ускорения J M и J H в сходственных точках натуры и модели находятся в одинаковых соотношениях, то есть существуют масштабы скоростей a v и ускорений а j:
При этом аV = const и a j = const. Кинематическое подобие обязательно включает в себя геометрическое подобие. Для динамического подобия необходимо, чтобы все силы, действующие в подобных точках модели и натуры на частицы жидкости, отличались между собой только постоянными масштабами при равенстве углов, характеризующих направление этих сил. Другими словами. явления динамически подобны, если физическая природа действующих на жидкость сил одинакова и векторы этих сил образуют геометрически подобные силовые многоугольники. На любую частицу жидкости в общем случае действуют следующие силы. Сила тяжести, пропорциональная плотности жидкости, ускорению свободного падения g и объёму W (или кубу линейного размера частицы l3):
Сила давления, пропорциональная гидродинамическому давлению p и площади S (или квадрату линейного размера частицы l2
Сила трения, пропорциональная вязкости частицы жидкости
Равнодействующая этих сил F, согласно второму закону И. Ньютона, равна произведению массы и ускорения:
Эта равнодействующая численно равна силе инерции:
Из условия подобия отношения всех пар сходственных сил натуры и модели равны:
где aF - масштаб сил, то есть число, показывающее во сколько раз силы в натуре (с индексом “н”) больше соответствующих сил в модели (с индексом “м”). Величины а, аv, аF называются масштабными множителями. Выбор всех масштабных множителей для подобных потоков не произволен, так как между ними существует определённая взаимосвязь. равнодействующая всех сил, действующих на произвольно взятую в потоке жидкости, выражается, согласно (10.6) в виде:
Следовательно, равнодействующие силы, действующие на 2 сходственные частицы жидкости потока в натуре и модели, равны:
Если выразить их соотношением в масштабных множителях, то получим:
где ap - масштабный множитель плотности р. Учитывая, что масштабный множитель ускорения выражается через масштабные множители скорости аj и длины а (геометрически масштабный множитель) в виде:
Получим
или
Зависимости (10. 10) и (10. 11) называют законом подобия Ньютона в масштабных множителях. Выражая масштабные множители соответствующими отношениями, получим:
или
где величина Критерий Ньютона можно записать и в другом виде, умножив числитель и знаменатель на l, и тогда при этом закон подобия Ньютона (10.10) в физических величинах запишется в виде:
Гидродинамическое (гидравлическое) подобие потоков Гидродинамическое (гидравлическое) подобие потоков обеспечивается равенством критериев Ньютона модели и натуры
Мтоды подобия и размерностей тесно связаны между собой, так как оба требуют отчётливого представления о механизме рассматриваемого явления. Однако для применения теории подобия нужны уравнения, определяющие процесс, а метод анализа размерностей применяется, когда уравнения процесса неизвестны. С помощью этого метода обрабатываются данные опытов и делают последующие обобщения. Начало общей теории этого метода было впервые положено в 1911 г. русским учёным Г. А. Федерманом (Известия Петербургского института, т. ХУ1, вып.1), доказавшим фундаментальную теорему подобия - Пи - теорему: всякое уравнение, выражающее некоторую физическую закономерность и поэтому не зависящее от выбора систем единиц измерения, связывающее собой N физических величин, среди которых величины обладают независимыми размерностями, может быть преобразовано в уравнение, связывающее (N- n) независимых безразмерных комплексов, составленных из упомянутых N физических величин. Суть этой теоремы заключается в следующем. Пусть W является функцией N размерных величин:
Можно доказать, что эту зависимость можно заменить критериальным уравнением П = f (1,1,.... 1, п1, п2.....пN-n) где роль размерных величин играют (N-n) безразмерных величин. Если основная система состоит из 3 единиц (масса, длина, время), то n=3 и вместо N величин рассматриваемое явление представляется в виде зависимости между безразмерными комплексами этих величин. Таким образом, восстановленное путём логических рассуждений уравнении, характеризующем данное явление, размерности величин в правых и левых частях, выраженные через размерности основных физических величин (масса М, длина l, время Т) должны соответствовать друг другу. Последовательность вычислений при составлении критериального уравнения (10.39) с использованием Пи -теоремы рассмотрена впримерах. Пример. необходимо установить зависимость для числа Рейнольдса. Решение. Исследуемое явление, т. е. режим движения, определяется средней скоростью V, а также диаметром трубы d. Для данного случая общая функциональная зависимость (10.39) выражается четырьмя переменными величинами через функцию П, являющуюся в данном случае безразмерной (число Рейнольдса): П = f (V, В соответствии с Пи - теоремой эту функцию можно выразить безразмерным комплексом N -3=4-3=1, то есть одной величиной
где x,y,z,k - показатели степени, подлежащие определению. Заменим величины в последнем уравнении их размерностями:
В левой части безразмерная величина выражена через размерности величин в нулевой степени. Приравнивая показатели степени у одинаковых оснований в левой и правой частях, получаем систему трёх уравнений:
Решение этой системы уравнений даёт следующие результаты:
Тогда искомая безразмерная функция
где m может иметь любое значение, отличающееся от нуля, так как безразмерное число в любой степени остаётся безразмерным. Проще принять m=1 и тогда получаем искомое число Рейнольдса:
П. Критерии гидродинамического подобия. Условием гидродинамического подобия является равенство на модели и в натурк отношений всех сил (тяжести, давления, инерции, трения поверхностного натяжения и др.). Вследствие физических особенностей этих сил практически недостижимо и необязательно. Поэтому устанавливают критерии подобия для частных случаев, когда в качестве преобладающей принимается какая-нибудь одна (главенствующая) из действующих сил. Критерий Фруда. Если преобладает действие сил тяжести, то необходимо выполнение условия, вытекающего из зависимости (10.8)
С учётом зависимостей (10.3) и (10.4) следует:
Следовательно, геометрически подобные потоки можно считать гидродинамически подобными, если будут равны числа Фруда для сходственных сечений обоих потоков:
При этом справедливы следующие соотношения для скоростей и расходов:
Масштабный множитель для времени:
При моделировании по Фруду справедливо равенство гидравлических уклонов (потерь на трение) IH = IM, что соответствует турбулентному режиму движения в квадратичной области сопротивления. Критерий Рейнольдса. при преобладающем действии сил трения необходимо выполнение условия, вытекающего из зависимости (10.9), по аналогии с предыдущим,
Таким образом, потоки будут гидродинамически подобны для движения жидкости при ламинарном режиме или в “гладкой” области сопротивления при турбулентном режиме, если будут равны числа Ренольдса для сходственных сечений обоих потоков: ReH = ReM, или Re = idem При
Критерий Эйлера. Если преобладает действие сил давления, то необходимо выполнение условий по аналогии с предыдущим:
где Eu - критерий Эйлера, который должен быть равен модели и натуры:
При соблюдении критерия Рейнольдса критерий Эйлера выполняется автоматически, и тогда
Критерий Вебера. При преобладающем действии сил поверхностного натяжения (капиллярных) необходимо выполнение условия:
Критерий Струхаля. Если преобладает действие сил инерции в условиях неустановившегося движения, то необходимо выполнение условия:
где St - критерий Струхаля, который должен быть равен для модели и натуры:
Соотношение для времени будет:
Критерий Маха. При преобладающем влиянии сжимаемости жидкости (обтекание тел потоком сжимаемой жидкости с большими скоростями) необходимо выыполнение условия:
где с - скорость распостранения звука в жидкости, а М - критерий Маха, который должен быть равен для модели и натуры: MH = MM или M= idem Критерий Архимеда. При действии архимедовских сил, возникающих вследствие разности плотностей двух сред (р - р) (подъёмная сила нагретого воздуха), необходимо выполнение условия:
Масштабные коэффициенты моделирования.
где Аr - критерий Архимеда, который должен быть равен для модели и натуры: ArH = ArM или Ar = idem Критерий Коши. Если преобладает действие упругих сил (гидравлический удар в трубах), то необходимо выполнение условия:
где Е - модуль упругости материала; Со - критерий Коши, который должен быть равен для модели и натуры: Сом = Сон или Со = idem Критерий Лагранжа. Этот критерий служит для установления подобия медленных течений вязких жидкостей и может быть представлен как произведение критериев Эйлера и Рейнольдса: La = EиRe = idem Сущетсвуют и другие критерии, относящиеся к частным случаям число Прандтля, число Ричардсона и др. Масштабные коэффициенты для наиболее часто встречающихся критериев подобия приведены в табл.10. 1.
III. Основные правила моделирования. При выборе масштаба модели с учётом принятого критерия необходимо соблюдать ряд условий, вытекающих из общих законов подобия: 1. Если поток в натуре турбулентный, то он должен быть турбулентным и на модели ( amin = (30... 50) где VH и RH - скорость, м/с, и гидравлический радиус, м, для натуры. 2. Если поток в натуре в спокойном состоянии (Fr < 1) или в бурном состоянии (Fr>1), то он должен быть соответственно в таком же состоянии и на модели. На соблюдение этого условия нужно обращать особое внимание при искажении масштаба модели. 3. При моделировании следует стремиться к геометрическому подобию шеороховатости, хотя иногда это практически трудно осуществимо (тогда возможно моделирование по условию 4. Если исследование связано с изучением движения насосов, то насосы на модели должны двигаться подобно натуре. 5. Если кавитация (разрыв сплошности струи) есть в натуре, то она должна быть в том же месте и на модели. 6. Влияние поверхностного натяжения должно быть настолько относительно малым, чтобы оно не мешало образованию волн. IV. Моделирование течений. Критериальное уравнение (10.40) для моделирования установившегося движения в напорных водоводах при отсутствии объёмных сил тяжести можно записать в виде:
где Условия моделирования для случая, когда неизвестна величина перепада давления Тогда Еи = При соблюдении критерия Рейнольдса критерий Эйлера выполняется автоматически и равен: Еи = тогда Гидравлический коэффициент трения может и не зависеть от числа Рейнольдса, что справедливо в области гидравлически шероховатых труб, называемой областью квадратичного сопротивления и характеризующейся большими числами Рейнольдса. Такая область потока, где Еи = idem
Если поток Re rp = где dm и Renp = Приведённые условия позволяют установить предельное уменьшение линейных размеров модели, то есть масштаб длин: a = Если принять линейный масштаб по условиям шероховатости Так как условия входа в трубопровод оказывают влияние на характеристики турбулентного потока, то необходимо учитывать длину участка стабилизации, которая равна 50 диаметрам. На расстоянии большем, чем длина участка стабилизации, характеристики турбулентности становятся соответствующими данной форме русла и его шероховатости. Кроме того, имеются рекомендации, определяющие минимальное расстояние, при котором не сказывается взаимное влияние местных сопротивлений. Для гладких водоводов (полиэтиленовые, стеклянные, деревянные, иногда бетонные и стальные) подобие устанавливается при условии: Re = idem
При протекании одной и той же жидкости в натуре и на модели (aj = 1 и ap = 1) связь между масштабами основных величин следующая:
Эти условия при малых масштабах выполнить трудно и тоэтому проводятся исследования в широком диапазоне чисел Re на моделях различных масштабов (масштабная серия исследования). Получаемые результаты позволяют перечислить модельные значения на натуру с учётом масштабных поправок на влияние сил вязкости:
Для напорных водоводов существует ещё одна автомодельная область ламинарного режима весьма медленных течений вязких жидкостей, когда можно пренебречь силами инерции. В этом случае условие подобия определяется критерием Лагранжа: La = ЕиRe = idem что приводит к условию: Еи = В открытых руслах движение воды происходит под действием сил тяжести и трения, и поэтому критериальное уравнение для физической величины в общем случае имеет вид:
а для установившегося движения
При равномерном движении составляющая сила тяжести уравновешивается силами трения и задача моделирования подобна задаче моделирования в напорных водоводах. При моделировании течений в открытых руслах (естественных и искусственных) обычно имеет место неравномерное движение. При моделировании турбулентных потоков, отвечающих квадратичной зоне сопротивления, исходят из критерия Фруда, считая, что такого рода движение обуславливается только силами тяжести. Как отмечено выше, такая область потока, где Для автомодельной области движения при Fr = idem ReM > Renp Значения Renp для квадратичной и переходной зон сопротивления, по аналогии с зависимостями (10.53) и (10.54), определяются из формул:
При этих условиях минимально допустимый линейный масштаб
В практике моделирования гидравлических процессов иногда применяют геометрическое искажение моделей. Это допускается в таких случаях: если нельзя обеспечить подобие шнроховатости, т. е. сопроитвление потока на модели больше, чем в натуре; когда размеры или расход воды в лаборатории не позволяют принять геометрические масштабы, обеспечивающие подобие; при необходимости обеспечить на модели достаточные глубины или подвижность насосов, соответствующие натуре. При перечисленных условиях не может быть выполнено полное геометрическое подобие, а поэтому не соблюдается и гидродинамическое подобие, то есть не будет подобия характеристик во всех точках пространства, занятого потоком. В то же время можно добиться подобия между средними скоростями, расходами и уклонами свободной поверхности. Для этого необходимо установить зависимости, которые позволят определить среднюю скорость, расход, уклон в натуре, если соответствующие величины замерены на модели, геометрически не подобной натуре. Такое условие подобия называется гидравлическим. При этом получается модель с двумя масштабами для линейных элементов: размеры живого (поперечного _сечения (в том числе и вертикальные h) уменьшены в аn раз, а апродольные в аi раз. Тогда соответствующие масштабные коэффициенты. ai = an / ai al = ah / ai aw = an / ai av = aa = ai Обычно искажение масштабов составляет 2-5, а в отдельных случаях до 10 раз. Детально вопросы моделирования с искажёнными масштабами, в том числе при пазмывах русла и движения наносов, рассмотрены в специальной литературе. При большом искажении вертикальных и горизонтальных масштабов, по предложению В. М. Маккавеева и А. Г. Аверкиева, применяется моделирование открытых потоков на воздушно- напорных моделях, при котором свободная поверхность заменяется жёсткой горизонтальной поверхностью. За пределами области автомодельности при Сопоставление результатов опытов на воздушно-напорной модели с данными, полученными на гидравлических моделях показывает, что мелкие воздушные напорные модели при искажении масштабов вполне могут заменить гидравлические модели для изучения плана течений и распределения скоростей потока в плане. При моделировании гидротехнических сооружений большое значение уделяется экспериментальному исследованию коэффициентов скорости, расхода, бокового и вертикального сжатия (струй) условий сопряжения бьефов, работы гасителей энергии, характеристик турбулентности в зоне гидравлического прыжка. и т. п. Обычно роль силы трения незначительна и преобладающее значение имеют силы тяжести, а поэтому моделирование ведётся по критерию Фруда, при котором соотношения между натурными и модельными параметрами потока подробно рассмотрены в пар. 10.2 Ряд исследователй считает, что для соблюдения условий автомодельности предельным является число Рейнольдса ReRnp> 5000....10 000. При этом условии расчётные коэффициенты протекания потока через водосливы, на перепадах, при истечении из-под щита и через др. подобные сооружения не зависят от числа Рейнольдса. Допустимое уменьшение размеров модели определяется условием:
где gH = gb удельный расход в натуре. Для наиболее характерных расходов gH = 3... 40 м2/с масштабы моделирования колеблются в минимально допустимых пределах а= 45....100. В отдельных случаях движения воды через гидросооружения необходимо учитывать и силу трения (быстротоки, водосливная поверхностб плотины большой высоты, сифоны и др.). Моделирование аэрации потока, кавитация и другие вопросы рассмотрены в специально литературе.
|

 , должны быть меньше, чем в натуре в а раз и, следовательно, в подобных потоках относительная шероховатость
, должны быть меньше, чем в натуре в а раз и, следовательно, в подобных потоках относительная шероховатость  R остаётся постоянной, такой же, как в натуре, то есть
R остаётся постоянной, такой же, как в натуре, то есть  H /
H / 



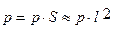
 , скорости её движения V и линейному размеру l:
, скорости её движения V и линейному размеру l:

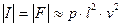

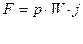





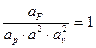

 т. е.
т. е. 
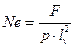 называется критерием Ньютона.
называется критерием Ньютона. , так как
, так как 

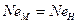

 :
:




 или
или 
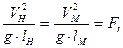

 или Fr = idem
или Fr = idem


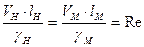
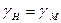 справедливы следующие соотношения скоростей, расходов, времени и гидравлического уклона:
справедливы следующие соотношения скоростей, расходов, времени и гидравлического уклона:


 или
или

 - коэффициент поверхностного натяжения, We - критерий Вебера, который должен быть равен для модели и натуры:
- коэффициент поверхностного натяжения, We - критерий Вебера, который должен быть равен для модели и натуры: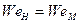 или
или 

 или
или 




 ReM>Rekp) при этом минимально допустимый масштаб модели:
ReM>Rekp) при этом минимально допустимый масштаб модели:
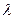 =idem)
=idem)
 - относительная шероховатость стенок водовода.
- относительная шероховатость стенок водовода. , входящего в критерий Эйлера, определяются числом Re= idem
, входящего в критерий Эйлера, определяются числом Re= idem




 - диаметр трубы и высота выступов шероховатости на модели.С учётом того, что в переходной зоне сопротвления изменение гидравлического коэффициента трения невилико, предельное число Рейнольдса может быть уменьшено ао формуле Зегжда:
- диаметр трубы и высота выступов шероховатости на модели.С учётом того, что в переходной зоне сопротвления изменение гидравлического коэффициента трения невилико, предельное число Рейнольдса может быть уменьшено ао формуле Зегжда:

 , то из зависимостей (10.55) и (10.56) при Renp = ReM определяются масштабные коэффициенты аv и аQ, а при Еи = idem будет справедливым соотношение
, то из зависимостей (10.55) и (10.56) при Renp = ReM определяются масштабные коэффициенты аv и аQ, а при Еи = idem будет справедливым соотношение 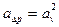
 f(Re)
f(Re)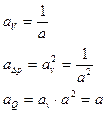
 и т. д.
и т. д.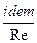


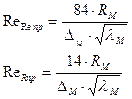
 - число Рейнольдса, подсчитанное по гидралическому радиусу.
- число Рейнольдса, подсчитанное по гидралическому радиусу.
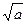
 3/2
3/2



