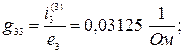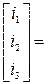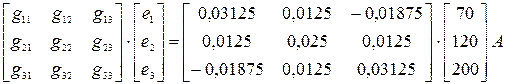Принцип взаимности
Принцип взаимности Из принципа наложения следует, что ток в “ к ”-ой ветви можно определить как алгебраическую сумму токов, вызванных каждым источником в отдельности:
В этом выражении gkk – входная проводимость “ к ”-ой ветви. Она определяется отношением тока в этой ветви к ЭДС в той же ветви при равных нулю ЭДС в остальных ветвях, т.е.:
Если стрелки ЭДС и тока в этой ветви направлены одинаково, то gkm – взаимная проводимость “ к ”-ой и “ m ”-ой ветви. Она определяется отношением тока “ к ”-ой ветви к ЭДС помещенной в “ m ”-ю ветвь при равных нулю ЭДС в остальных ветвях, т.е:.
Так как стрелки токов в “ к ”-ой и “ m ”-ой ветвях в общем случае ставятся произвольно, а ЭДС в “ m ”-ой ветви поставить по стрелке тока в этой ветви, то gkm – алгебраическое число. Принцип взаимности выражается равенством
Этот принцип можно проиллюстрировать двумя режимами работы электрической цепи, если в ней выделить ветви “ к ” и “ m ”.
Если ek= em= e, то справедливо равенство
Пример 1.
В электрической цепи необходимо определить входные и взаимные проводимости, если
Решение. Выбираем (произвольно) направления токов в ветвях и обозначаем их. Поместим в ветвь 1 источник ЕДС
Вычисляем
Помещаем в ветвь 2 источник ЕДС е 2=10 В как показано на рисунке и вычислим токи, вызванные этим источником.
Вычисляем
Помещаем в ветвь 3 источник ЕДС е 3=10 В как показано на рисунке и вычислим токи, вызванные этим источником.
Вычисляем
Пример 2.
В электрической цепи, рассмотренной в примере 1, поменяем источники ЭДС е 1=70 В; е 2=120 В; е 3=200 В. Требуется вычислить токи в ветвях цепи.
Решение. Составим матрицу входных и взаимных проводимостей, взяв их значения из расчета, проведенного в примере 1.
Тогда, применяя принцип наложения вычислим вектор токов в ветвях умножением матрицы проводимости на вектор ЭДС.
|

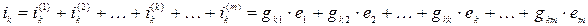 .
. .
. >0.
>0. .
.





 ,
,  .
. , как показано на рисунке и вычислим токи, вызванные этим источником.
, как показано на рисунке и вычислим токи, вызванные этим источником.

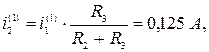

 :
:






 :
:



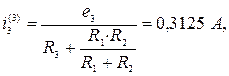


 :
: