for i:=0 to n do
Begin
s:=inputbox('введите коэффициенты','a'+IntToStr(i),'0');
a[i]:=StrToint(s);
x:=strtofloat(edit2.text);
p:=a[0];
End;
for i:=1 to n do
p:=p*x+a[i];
Label2.Caption:='Значение полинома '+IntToStr(p);
End;
Таблица 9 - Индивидуальные варианты лабораторной работы №7
| № В
| Варианты индивидуальных заданий
|
|
| Найти наименьший элемент последовательности  и его номер. и его номер.
|
|
| Вычислить сумму элементов последовательности 
|
|
| По заданному полиному  найти коэффициенты полинома Q(x)=P(x). найти коэффициенты полинома Q(x)=P(x).
|
|
| По заданному полиному  ) найти коэффициенты полинома ) найти коэффициенты полинома 
|
|
| По заданной последовательности  построить последовательность построить последовательность  , исключив из заданной последовательности нулевые элементы. Определить количество оставшихся элементов. , исключив из заданной последовательности нулевые элементы. Определить количество оставшихся элементов.
|
Продолжение таблицы 9
|
| Дана последовательность целых чисел  . Получить новую последовательность, выбросив из исходной элементы со значением max( . Получить новую последовательность, выбросив из исходной элементы со значением max( ). ).
|
|
| По заданной последовательности  (n<=20) построить две последовательности (n<=20) построить две последовательности  и и  , элементы которых определяются условиями: , элементы которых определяются условиями:

|
|
| Дана последовательность  (n<=20). Сдвинуть циклически последовательность на один элемент влево (например, из последовательности 5 8 3 4 10 получить 8 3 4 10 5). (n<=20). Сдвинуть циклически последовательность на один элемент влево (например, из последовательности 5 8 3 4 10 получить 8 3 4 10 5).
|
|
| Найти сумму элементов последовательности  (n<=30), начиная от первого отрицательного элемента и до конца последовательности. (n<=30), начиная от первого отрицательного элемента и до конца последовательности.
|
|
| Дана последовательность вещественных чисел  (n<=20). Вычислить (n<=20). Вычислить 
|
|
| В последовательности  (n<=25) заменить все отрицательные элементы их квадратами, а положительные – кубами. (n<=25) заменить все отрицательные элементы их квадратами, а положительные – кубами.
|
|
| В последовательности  (n<=30) сосчитать число отрицательных и число положительных элементов. (n<=30) сосчитать число отрицательных и число положительных элементов.
|
|
| Дана последовательность целых чисел  (n<=15). Вычислить (n<=15). Вычислить  , где m – либо номер первого отрицательного элемента, либо n, если отрицательных элементов нет. , где m – либо номер первого отрицательного элемента, либо n, если отрицательных элементов нет.
|
|
| Дана последовательность из n (n<=20) различных целых чисел. Найти сумму чисел этой последовательности, расположенных между максимальным и минимальным числами, включая эти числа.
|
|
| Даны две последовательности по n целых чисел в каждой (n<=10). Найти наименьшее среди тех чисел первой последовательности, которые не входят во вторую последовательность.
|
|
| Даны целые числа а1,…,а50. Получить последовательность b1,…,b50, которая отличается от исходной тем, что все члены удвоены.
|
|
| Даны натуральные числа n, a1, a2, …,an. Определить количество ak последовательности a1,a2,…,an, являющихся нечётными числами.
|
Продолжение таблицы 9
|
| Даны натуральные числа n, a1, a2, …,an. Определить количество ak последовательности a1,a2,…,an, кратных 3 и не кратных 5.
|
|
| Даны натуральные числа n, a1, a2, …,an. Определить количество ak последовательности a1,a2,…,an, являющихся квадратами чётных чисел.
|
|
| Даны натуральные числа n, a1, a2, …,an. Определить количество ak последовательности a1,a2,…,an, удовлетворяющих условию
 . .
|
|
| Даны натуральные числа n, a1, a2, …,an. Определить количество ak последовательности a1,a2,…,an, удовлетворяющих условию
 . .
|
|
| Даны натуральные числа n, q1, q2,…, qn. найти те члены qi последовательности q1, q2,…, qn которые являются удвоенными нечётными числами.
|
|
| Даны натуральные числа n, q1, q2,…, qn. найти те члены qi последовательности q1, q2,…, qn, которые при делении на 7 дают остаток 1,2 или 5.
|
|
| Даны натуральные числа n, a1, a2, …,an. В последовательности a1, a2,…,an получить сумму положительных и число отрицательных членов.
|
|
| Дано натуральное число n. Получить сумму тех чисел, которые являются удвоенными нечётными. При отсутствии таких чисел искомая сумма равна нулю.
|
|
| Даны целые числа а1,…,а50. Получить сумму тех чисел данной последовательности, которые кратны 5.
|
|
| Даны целые числа а1,…,а50. Получить сумму тех чисел данной последовательности, которые нечётны и отрицательны.
|
|
| Даны целые числа а1,…,а50. Получить сумму тех чисел данной последовательности, которые удовлетворяют условию  . .
|
Продолжение таблицы 9
|
| Даны натуральное число n, действительные числа a1, a2, …,an. в последовательности a1, a2, …,an все отрицательные члены увеличить на 0.5, а все неотрицательные заменить на 0.1.
|
|
| Даны натуральное число n, действительные числа x1,…xn. В последовательности x1,…xn все члены, меньшие двух, заменить нулями.
|
1.8 Обработка двумерных массивов
Цель:Умение использовать двумерные массивы.
Описание массива может быть дано разными способами.
В первом способе это делается в разделе описания переменных. При этом необходимо указать: имя массива, границы изменения индексов, тип элементов массива.
Таким образом, вся информация о массиве приводится сразу.
Var a: array[1..2,1..3] of real;
Здесь объявляется двумерный массив с именем а, состоящий из шести элементов вещественного типа. В квадратных скобках указываются границы изменения каждого индекса, разделенные запятой.
В данном случае первый индекс принимает значения 1 или 2, а второй изменяется от 1 до 3.
При втором способе описания определяется новый тип данных, представляющих собой многомерный массив с заданными границами изменения индексов, а затем описываются переменные этого типа.
Например,
Type matrix = array[1..5,1..5] of integer;
Var a,b: matrix;
В этом примере определяются данные типа matrix (это массивы, состоящие из пяти строк и пяти столбцов целых чисел) и вводятся две переменные a и b этого типа.
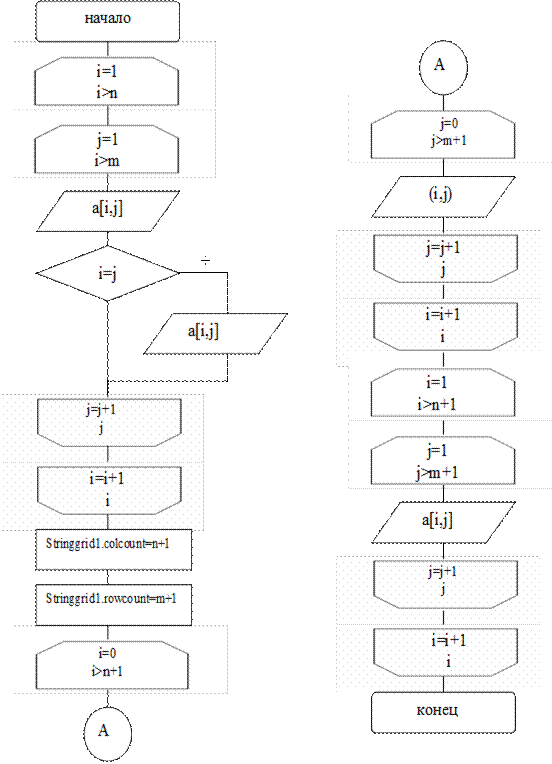
Задание1: Даны натуральное число n, действительная матрица  . Получить последовательность элементов главной диагонали а11, а22,…, аnn.
. Получить последовательность элементов главной диагонали а11, а22,…, аnn.
Технология выполнения задания
Постановка задачи: Создать приложение для вывода последовательности элементов главной диагонали а11, а22,…, аnn, данной матрицы.
Математическая модель представляется так: исходные данные – n,,  , результат – а11, а22,.. аnn.
, результат – а11, а22,.. аnn.
Алгоритм решения задачи: запишем алгоритм решения поставленной задачи с помощью блок-схемы (описываем только процедуру вычисления значения функции).
Программа: Установите компоненты на форме и измените свойство Caption для каждого компонента в соответствии с рисунком 18.
Для компонента BitBtn1 (кнопка Закрыть) в инспекторе объектов измените свойство Kind – bkClose. Для вывода двумерного массива используют компонент StringGrid1, находящийся на вкладке Standart. Компонент StringGrid1 предназначен для создания таблиц.
Данный компонент использует ряд свойств и методов:
1) Сells[i,j] – двухмерный массив ячеек, каждая из которых содержит произвольный текст;
2) ColСount – содержит количество колонок таблицы;
3) RowCount - содержит количество рядов таблицы;
4) FixedCouls – определяет количество колонок фиксированной зоны, заголовков столбцов;
5) FixedRows – определяет количество рядов фиксированной зоны, заголовков строк;
6) Optins.gotabs – свойство разрешающее перемещение между ячейками (если установлено значение true);
7) Options.always.show.editing – свойство разрешающее редактирование таблицы (если установлено значение true);



Рисунок 18 - Образец размещения компонент на форме
Двойным щелчком по компоненту Button1 (кнопка Вычислить) автоматически создается в окне кода стандартная структур. В данную структуру впишите часть программы (у каждого варианта своя индивидуальная часть программы). Для задания 1 эта часть выглядит следующим образом:
procedure TForm1.Button1Click(Sender: TObject);
const n=2; m=3;
var a:array[1..n,1..m] of integer;
s:string; i,j,b,min: integer;
Begin
for i:=1 to n do
for j:=1 to m do
Begin
s:=inputbox('введите','a'+IntToStr(i)+IntToStr(j),'0');
a[i,j]:=StrToInt(s);
if i=j then
ListBox1.Items.Add('a['+IntToStr(i)+','+IntToStr(j)+']='+IntToStr(a[i,j]));
End;
StringGrid1.ColCount:=n+1;
StringGrid1.RowCount:=m+1;
for i:=0 to n+1 do
for j:=0 to m+1 do
StringGrid1.Cells[i,j]:='('+IntToStr(i)+';'+IntToStr(j)+')';
for i:=1 to n+1 do
for j:=1 to m+1 do
StringGrid1.Cells[i,j]:=IntToStr(a[i,j]);
End;
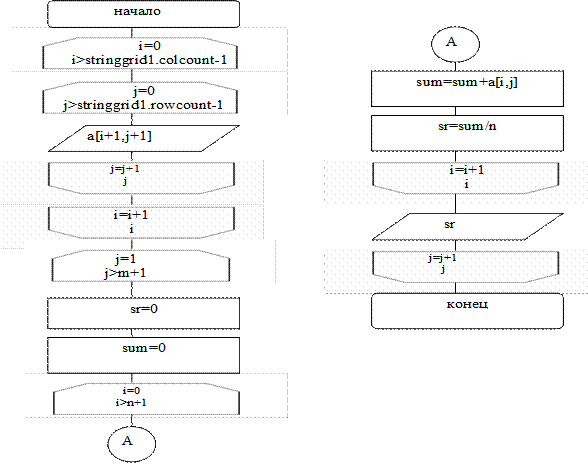
Задание 2:Даны натуральные натуральное число n, действительная матрица размера n  . Вывести матрицу на экран. Найти среднее арифметическое каждого из столбцов.
. Вывести матрицу на экран. Найти среднее арифметическое каждого из столбцов.
Технология выполнения задания
Постановка задачи: Математическая модель представляется так: исходные данные – n,  , результат – а11, а22,.. аnn.
, результат – а11, а22,.. аnn.
Алгоритм решения задачи:Запишем алгоритм решения поставленной задачи с помощью блок-схемы (описываем только процедуру вычисления значения функции).
Программа: Установите компоненты на форме и измените свойство Caption для каждого компонента.
Для компонента BitBtn1 (кнопка Закрыть) в инспекторе объектов измените свойство Kind – bkClose.
Установите в свойстве ColСount значение 2, RowCount – 3, Fixed-Couls значение 0, FixedRows – 0, optins.gotabs –значение true, Options.always.show.editing –значение true;
Двойным щелчком по компоненту Button1 (кнопка Вычислить) автоматически создается в окне кода стандартная структур. В данную структуру впишите часть программы (у каждого варианта своя индивидуальная часть программы). Для задания 2 эта часть выглядит следующим образом:
procedure TForm1.Button1Click(Sender: TObject);
const n=2; m=3;
var a: array[1..n,1..m] of integer;
s:string; i,jsum: integer; sr: real;
Begin
for i:=0 to stringgrid1.rowcount-1
for j:=0 to stringgrid1.colcount-1
a[i+1,j+1]:=strtoint(stringgrid1.cells[i,j]);
for j:=1 to m do
Begin
sr:=0;
sum:=0;
for i:=1 to n do
sum:=sum+ a[i,j];
sr:=sum/n;
ListBox1.Items.Add(FloatToStr(sr));
End;
Таблица 10 - Индивидуальные варианты лабораторной работы №8
| № В
| Варианты индивидуальных заданий
|
|
| Решить систему линейных уравнений с верхней треугольной матрицей

|
|
| Дана квадратная матрица А пятого порядка. Найти А2.
|
|
| Определить, является ли заданная квадратная матрица пятого порядка, составленная из целых чисел, симметричной относительно главной диагонали.
|
Продолжение таблицы 10
|
| Вычислить норму квадратной матрицы А пятого порядка по формуле  . .
|
|
| Вычислить сумму всех элементов квадратной матрицы пятого порядка, лежащих не ниже главной диагонали.
|
|
| Вычислить произведение матрицы А на вектор b. Элементы результирующего вектора c=A*b определяются следующим образом:

|
|
| Вычислить элементы матрицы С, являющейся произведением нижней треугольной матрицы пятого порядка на верхнюю треугольную матрицу того же порядка.
|
|
| Вычислить элементы матрицы С, являющейся суммой нижней треугольной матрицы пятого порядка и верхней треугольной матрицы того же порядка.
|
|
| Проверить, является ли исходная матрица, составленная из целых чисел, нижней треугольной. Напечатать соответствующее сообщение.
|
|
| Определить среднее арифметическое отдельно от всех положительных и всех отрицательных элементов матрицы А.
|
|
| Найти максимальный по модулю элемент матрицы и номер строки и столбца, в котором он находится.
|
|
| Дана несимметричная прямоугольная матрица. Сформировать транспонированную к ней матрицу.
|
|
| Вычислить суммы элементов каждой строки матрицы В(5×4), определить наименьшее значение среди этих сумм и номер соответствующей строки.
|
Продолжение таблицы 10
|
| Осуществить в исходной матрице Y пятого порядка перестановку элементов, несимметричных относительно главной диагонали.
|
|
| Переписать первые элементы каждой строки матрицы Z(4×5), большие заданной величины с, в вектор b(4). Если в строке нет такого элемента, то в вектор b записать 0.
|
|
| Дана действительная матрица размера m´n. Вывести матрицу на экран. Определить числа b1,…,bm равные суммам элементов строк.
|
|
| Дана действительная матрица размера m´n. Вывести матрицу на экран. Определить числа b1,…,bm равные произведениям элементов строк.
|
|
| Дана действительная матрица размера m´n. Вывести матрицу на экран. Определить числа b1,…,bm равные наименьшим значениям элементов строк.
|
|
| Дана действительная матрица размера m´n. Вывести матрицу на экран. Определить числа b1,…,bm равные значениям средних арифметических элементов строк.
|
|
| Дана действительная матрица размера m´n. Вывести матрицу на экран. Определить числа b1,…,bm равные разностям наибольших и наименьших значений элементов строк.
|
|
| Даны натуральное число n, действительная матрица размера n´9. Вывести матрицу на экран. Найти средне арифметическое каждого из столбцов;
|
|
| Даны целые числа а1, а2, а3. Получить целочисленную матрицу  , для которой , для которой  . .
|
|
| Даны действительные числа а, …,а; b, …,b. Получить действительную матрицу  , для которой , для которой  . .
|
Продолжение таблицы 10
|
| Дана действительная матрица 18´n. Вывести матрицу на экран. Найти значение наибольшего по модулю элемента матрицы.
|
|
| Получить  - целочисленную матрицу для которой. - целочисленную матрицу для которой. 
|
|
| Дана действительная матрица размера m´n. Вывести матрицу на экран. Найти сумму наибольших значений элементов её строк.
|
|
| Дано натуральное число n. Выяснить сколько положительных элементов содержит матрица  , если , если  . Вывести матрицу на экран. . Вывести матрицу на экран.
|
|
| Дана действительная матрица n´m, в которой не все элементы равны нулю. Получить новую матрицу путём деления всех элементов данной матрицы на её наибольший по модулю элемент.
|
|
| Дана действительная квадратная матрица порядка 12. Заменить нулями все её элементы, расположенные на главной диагонали.
|
|
| Дана действительная матрица размера 6´9. Вывести матрицу на экран. Найти среднее арифметическое наибольшего и наименьшего значений её элементов.
|
1.9 Табулирование функции двух переменных
Цель:Умение представлять результаты вычисления значения функции двух переменных в табличном виде.
Рассмотрим тему на примерах.
Задание: На интервалах  с шагом
с шагом  и
и  с шагом
с шагом  протабулировать функцию
протабулировать функцию  , где х - произвольное число.
, где х - произвольное число.
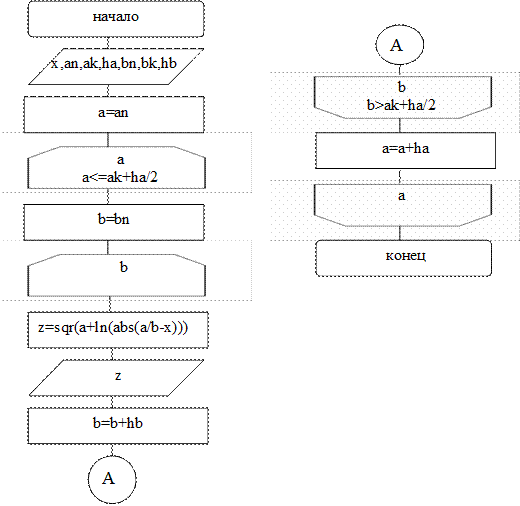
Технология выполнения задания
Постановка задачи: Создать приложение вычисления значений функции z.
Математическая модель представляется так: исходные данные – x,a,b, результат – z вычисляется для каждого a и b на интервалах  с шагом
с шагом  и
и  с шагом
с шагом  .
.
Алгоритм решения задачи: запишем алгоритм решения поставленной задачи с помощью блок-схемы (описываем только процедуру вычисления значения функции).
Программа: Установите компоненты на форме и измените свойство Caption для каждого компонента в соответствии с рисунком 19.
 Рисунок 19 - Образец размещения компонентов на форме
Рисунок 19 - Образец размещения компонентов на форме
Для компонента BitBtn1 (кнопка Закрыть) в инспекторе объектов измените свойство Kind – bkClose.
Двойным щелчком по компоненту Button1 (кнопка Вычислить) автоматически создается в окне кода стандартная структур. В данную структуру впишите часть программы (у каждого варианта своя индивидуальная часть программы). Для данного задания эта часть выглядит следующим образом:
procedure TForm1.Button1Click(Sender: TObject);
var z,an,ak,ha,bn,bk,hb,a,b,x:real;
s:string;
Begin
x:=StrToFloat(Edit1.Text);
s:=inputbox('ввод данных','an','o');
an:=StrToFloat(s);
s:=inputbox('ввод данных','ak','o');
ak:=StrToFloat(s);
s:=inputbox('ввод данных','ha','o');
ha:=StrToFloat(s);
s:=inputbox('ввод данных','bn','o');
bn:=StrToFloat(s);
s:=inputbox('ввод данных','bk','o');
bk:=StrToFloat(s);
s:=inputbox('ввод данных','hb','o');
hb:=StrToFloat(s);
a:=an;
while a<=ak+ha/2 do
Begin
b:=bn;
Repeat
z:=sqr(a+ln(abs(a/b-x)));
s:='a='+FloatToStr(a)+' b='+FloatToStr(b)+' z='+FloatToStr(z);
ListBox1.Items.Append(s);
b:=b+hb;
until b>bk+hb/2;
a:=a+ha;
End;
End;
Таблица 11 - Индивидуальные варианты лабораторной работы №9
| № В
| Варианты индивидуальных заданий
|
|
| На интервалах  с шагом с шагом  и и  с шагом с шагом  для каждого а и b протабулировать функцию для каждого а и b протабулировать функцию  , где х - любое действительное число. , где х - любое действительное число.
|
Продолжение таблицы 11
|
| На интервалах  с шагом с шагом  и и  с шагом с шагом  для каждого а и b протабулировать функцию для каждого а и b протабулировать функцию
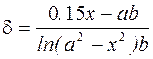 , где х - любое действительное число. , где х - любое действительное число.
|
|
| На интервалах  с шагом с шагом 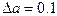 и и  с шагом с шагом  для каждого а и b протабулировать функцию для каждого а и b протабулировать функцию

|
|
| На интервалах  с шагом с шагом  и и  с шагом с шагом  для каждого а и b вычислить для каждого а и b вычислить  ,х=0.792 ,х=0.792
|
|
| На интервалах  с шагом с шагом  и на интервала и на интервала  с шагом с шагом  для каждого а и b протабулировать функцию для каждого а и b протабулировать функцию  . .
|
|
| На интервалах  с шагом с шагом  и и  для каждого а и z вычислить для каждого а и z вычислить  , причём, если , причём, если  , ,  , иначе , иначе  . .
|
|
| На интервалах 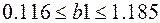 с шагом с шагом  и и  с шагом с шагом  для каждого а и b вычислить значения функции для каждого а и b вычислить значения функции  . .
|
|
| На интервалах  с шагом с шагом  и и  с шагом с шагом  для каждого а и b протабулировать функцию для каждого а и b протабулировать функцию  , причём х=0.44. , причём х=0.44.
|
|
| На интервалах  с шагом с шагом  и и  с шагом с шагом  для каждого а и b вычислить для каждого а и b вычислить  , причём х=0.087. , причём х=0.087.
|
|
| На интервалах  с шагом с шагом  и и  с шагом с шагом 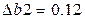 для каждого а и b вычислить значения для каждого а и b вычислить значения  , где х=1.44 , где х=1.44
|
Продолжение таблицы 11
|
| На интервалах 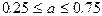 с шагом с шагом  и и  с шагом с шагом  для каждого а и b протабулировать функцию для каждого а и b протабулировать функцию  , причём, х= 0.416. , причём, х= 0.416.
|
|
| На интервалах  с шагом с шагом  и и  с шагом с шагом  для каждого а и b протабулировать функцию для каждого а и b протабулировать функцию  , где х - любое положительное число. , где х - любое положительное число.
|

 и его номер.
и его номер.

 найти коэффициенты полинома Q(x)=P(x).
найти коэффициенты полинома Q(x)=P(x).
 ) найти коэффициенты полинома
) найти коэффициенты полинома 
 построить последовательность
построить последовательность  , исключив из заданной последовательности нулевые элементы. Определить количество оставшихся элементов.
, исключив из заданной последовательности нулевые элементы. Определить количество оставшихся элементов.
 . Получить новую последовательность, выбросив из исходной элементы со значением max(
. Получить новую последовательность, выбросив из исходной элементы со значением max( ).
).
 и
и  , элементы которых определяются условиями:
, элементы которых определяются условиями:


 , где m – либо номер первого отрицательного элемента, либо n, если отрицательных элементов нет.
, где m – либо номер первого отрицательного элемента, либо n, если отрицательных элементов нет.
 .
.
 .
.
 .
.
 . Получить последовательность элементов главной диагонали а11, а22,…, аnn.
. Получить последовательность элементов главной диагонали а11, а22,…, аnn. , результат – а11, а22,.. аnn.
, результат – а11, а22,.. аnn.



 . Вывести матрицу на экран. Найти среднее арифметическое каждого из столбцов.
. Вывести матрицу на экран. Найти среднее арифметическое каждого из столбцов.

 .
.

 , для которой
, для которой  .
.
 , для которой
, для которой  .
.
 - целочисленную матрицу для которой.
- целочисленную матрицу для которой. 
 , если
, если  . Вывести матрицу на экран.
. Вывести матрицу на экран.
 с шагом
с шагом  и
и  с шагом
с шагом  протабулировать функцию
протабулировать функцию  , где х - произвольное число.
, где х - произвольное число.

 Рисунок 19 - Образец размещения компонентов на форме
Рисунок 19 - Образец размещения компонентов на форме с шагом
с шагом  и
и  с шагом
с шагом  для каждого а и b протабулировать функцию
для каждого а и b протабулировать функцию  , где х - любое действительное число.
, где х - любое действительное число.
 с шагом
с шагом 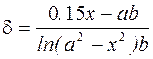 , где х - любое действительное число.
, где х - любое действительное число.
 с шагом
с шагом 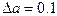 и
и 
 с шагом
с шагом  и
и  с шагом
с шагом  для каждого а и b вычислить
для каждого а и b вычислить  ,х=0.792
,х=0.792
 с шагом
с шагом  и на интервала
и на интервала  с шагом
с шагом  для каждого а и b протабулировать функцию
для каждого а и b протабулировать функцию  .
.
 с шагом
с шагом  и
и  для каждого а и z вычислить
для каждого а и z вычислить  , причём, если
, причём, если  ,
,  , иначе
, иначе  .
.
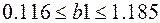 с шагом
с шагом  и
и  с шагом
с шагом  для каждого а и b вычислить значения функции
для каждого а и b вычислить значения функции  .
.
 с шагом
с шагом  и
и  , причём х=0.44.
, причём х=0.44.
 с шагом
с шагом  и
и  с шагом
с шагом  для каждого а и b вычислить
для каждого а и b вычислить  , причём х=0.087.
, причём х=0.087.
 с шагом
с шагом  и
и  с шагом
с шагом 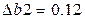 для каждого а и b вычислить значения
для каждого а и b вычислить значения  , где х=1.44
, где х=1.44
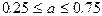 с шагом
с шагом  и
и  , причём, х= 0.416.
, причём, х= 0.416.
 , где х - любое положительное число.
, где х - любое положительное число.



