Свойства средней арифметической. Способы ее исчисления.
Свойства средней арифметической: 1. Если xi=c, где с – постоянная величина, то средняя арифметическая будет равна с; 2. Сумма отклонений значений признака от его средней арифметической равна 0, т.е. 3. Если из всех значений признака вычесть постоянную величину с, то средняя арифметическая уменьшится на эту величину с:
4. От уменьшения или увеличения частот
5. Если все индивидуальные значения признака уменьшить или увеличить в d раз, то величина средней арифметической также уменьшится или увеличится в d раз.
Способ моментов (метод отсчета от условного нуля)используется в случае вариационных рядов с равными интервалами. Согласно этому методу среднюю арифметическую взвешеннную можно вычислить: Способы исчисления: В дискретном ряду:
В вариационном ряду:
|
;
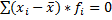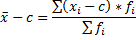
каждого значения признака в м раз величина средней арифметической не изменится:
, момент первого порядка. d – величина интервала, c- значение середины интервала, находящегося в центре ряда (если количество интервалов нечетное) или середину интервала с наибольшей частотой также из центра ряда (при четном количестве интервалов в центре ряда будут находится два интервала).
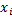
=1360/25=54,4 кв. м.
