Относительные показатели вариации. Их значение в статистическом анализе.
Относительные показатели вариации используются для сравнения степени вариации: · Одного признака в разных совокупностях; · Разных признаков в одной совокупности; 1. Коэффициент оссиляции 2. Отнсительное линейное отклонение 3. Коэффициент вариации При анализе рядов распределения проводится оценка симметричности и крутизны распределения. Симметричное распределение Распределение является симметричным, если частоты двух любых вариант, равноотстоящих в обе стороны от центра распределения, равны между собой. Симметричное распределение: Правосторонняя ассиметрия: Левосторонняя ассиметрия: Чем больше разница между средней арифметической и модой (медианой), тем больше асимметрия ряда. Степень ассиметрии: Моментный коэффициент асимметрии
Коэффициент асимметрии изменяется от –3 до +3. Если As>;0, то правосторонняя ассиметрия. При этом выполняется соотношение Если As<;0, то асимметрия левосторонняя. При этом На практике асимметрия считается значительной, если коэффициент асимметрии превышает по модулю 0,25. Если превышает по модулю 0,5, то ассиметрия значительная. Крутизна распределения: Эксцесс представляет собой вершины распределения вверх или вниз от вершины нормального распределения. Коэффициент эксцесса рассчитывается по формуле
где
16. Виды дисперсии. Правило сложения дисперсий. Свойства дисперсии. + 17. Использование метода группировок для изучения взаимосвязи между социально-экономическими явлениями. Эмпирическое корреляционное отношение. Виды дисперсий: Эмпирический коэффициент детерминации показывает, какая доля в общей дисперсии показателя приходится на дисперсию, возникающую в результате вариации группировочного признака. Ход вычисления: 1. Определяется общее среднее значение показателя по формуле средней арифметической, либо простой, либо взвешенной. 2. Вычисляется общая дисперсия: 3. Рассчитываются групповые средние. 4. Определяются внутригрупповые дисперсии: 5. Вычисляется средняя из внутригрупповых дисперсий: 6. Межгрупповая дисперсия: 7. Правило сложения дисперсий: 8. Эмпирический коэффициент детерминации: 9. Эмпирическое корреляционное отношение: Свойства дисперсии: o Если xi=c, где с – постоянная величина, то дисперсия будет равна нулю; o Если из всех значений признака вычесть постоянную величину с, то дисперсия от этого не изменится:
o Если все индивидуальные значения признака уменьшить в d раз, то дисперсия уменьшится в d2 раз:
На приведенных свойствах дисперсии основан один из методов ее расчета – способ моментов. Согласно ему дисперсию можно вычислить по следующей формуле (применяется только в случаях с равными интервалами!)
Где d – величина интервала, c- значение середины интервала, находящегося в центре ряда (если количество интервалов нечетное) или середину интервала с наибольшей частотой также из центра ряда (при четном количестве интервалов в центре ряда будут находится два интервала).
|




 - совокупность неоднородна.
- совокупность неоднородна. =Ме = Мо.
=Ме = Мо. , где
, где 
 ,
, - центральный момент четвертого порядка,
- центральный момент четвертого порядка,  или
или  . При нормальном распределении
. При нормальном распределении  =3, эксцесс нормального распределения равен 0. Обычно, если эксцесс положителен, то распределение островершинное, если отрицательный – то плосковершинное.
=3, эксцесс нормального распределения равен 0. Обычно, если эксцесс положителен, то распределение островершинное, если отрицательный – то плосковершинное. либо
либо  . Она характеризует вариацию значений признака за счет всех факторов, как положенного в основу группировки, так и не учтенных, но действующих.
. Она характеризует вариацию значений признака за счет всех факторов, как положенного в основу группировки, так и не учтенных, но действующих.
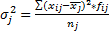 . Они характеризуют вариацию значений исследуемого признака внутри групп независимо от того, какое значение принимает группировочный признак.
. Они характеризуют вариацию значений исследуемого признака внутри групп независимо от того, какое значение принимает группировочный признак.
 . Межгрупповая дисперсия характеризует вариацию значений исследуемого признака за счет действия на него только группировочного признака.
. Межгрупповая дисперсия характеризует вариацию значений исследуемого признака за счет действия на него только группировочного признака. . Проверяется точность вычислений, или найти по двум компонетам неизвестную.
. Проверяется точность вычислений, или найти по двум компонетам неизвестную.
 . Изменяется от о до 1. 0 – связи нет. 1- наличие функциональной зависимости между признаками, при которой значения исследуемого показателя полностью полностью определяются значениями группировочного признака. Чем ближе к единице, тем теснее связь.
. Изменяется от о до 1. 0 – связи нет. 1- наличие функциональной зависимости между признаками, при которой значения исследуемого показателя полностью полностью определяются значениями группировочного признака. Чем ближе к единице, тем теснее связь.





