Некоторые сведения из векторного анализа.
Математические модели электрического и магнитного полей обычно представлены в векторной форме, поскольку эти поля представляются в виде сил, действующих в определенных направлениях вдоль касательных к линиям, которые называются силовыми линиями полей. Для математических операций с полями используется векторный анализ. Минимальные сведения и соотношения, которые изложены в настоящем разделе. Прежде, чем приступить к изучению основного материала теории электромагнетизма, полезно ознакомиться с некоторыми соотношениями из векторного анализа, так как математические модели объектов в электромагнитной теории удобно представить в векторном виде. Обратимся к известной дифференциальной операции, операции градиента некоторой скалярной величины j. Градиентом называют вектор имеющий направление быстрейшего увеличения величины и равный по модулю производной по этому направлению Ñ- оператор Гамильтона,
или
В качестве примера можно привести градиент атмосферного давления над поверхностью Земли.
На Рис. 1 представлены изобары — плоскости одинакового давления атмосферы над Земной поверхностью при пересечении их плоскостью XY. В этом случае они выглядят в виде параллельных линий. Поскольку Р0>Р1>Р2>Р3>Р4 вектор градиента
так как
Векторное представление удобно тем, что позволяет заранее не использовать какие-либо координаты, а оперировать непосредственно с вектором, поэтому можно использовать интегральное представление оператора Гамильтона и применить его для величин векторных.
тогда
Оператор Гамильтона называют оператором объемного дифференцирования
Рис. 2 Объем V и стягивающая его поверхность S. Здесь предполагается V - бесконечно малый объем, на котором имеет место точка, в которой вычисляются результаты объемного дифференцирования. Объем V окружает замкнутую поверхность S, dS - ее элемент, умноженный на единичный вектор n (сокращенно ее часто обозначают dS) Единичный вектор n - нормален к поверхности S. lim обозначает, что поверхность стягивается к точке на поверхности S(r) (Рис. 2). Известны три основные операции grad, div, rot.
В декартовых координатах величина
определяет циркуляцию вектора A вихрь вектора вдоль контура L. (Рис. 3).
Рис. 3 Циркуляция вектора. На рис. 3 dl - единичный вектор вдоль касательной к контуру L. Если объект действия оператора Гамильтона - V фиксирован, то с ним можно производить операции, как с обычным вектором, в декартовых координатах,
тогда
Разложение по ортам
Оператор Гамильтона является и дифференциальным оператором и поэтому в соответствии с правилом дифференцирования
следует
Используя это обстоятельство можно вывести ряд формул
учитывая что,
или
Следует заметить, что используя дифференциальные операции можно получить формулы:
так как векторное или скалярное произведение трех векторов, из которых два одинаковых обращается в 0. Важная теорема Стокса, которая формулируется следующим образом "Циркуляция вектора по замкнутому контуру равна потоку вихря вектора через поверхность ограниченную этим контуром", что можно представить в виде выражения
В теории электромагнетизма используют теорему, которая получила название Остроградского-Гаусса. Формулируется она следующим образом "Поток вектора
Это соотношение может быть получено, как следствие более общей теоремы Остроградского.
|










 (2)
(2) (3)
(3)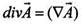 носит в математике название "расхождение" и представляет собой поток вектора
носит в математике название "расхождение" и представляет собой поток вектора  через замкнутую вокруг источника вектора односвязную поверхность S.
через замкнутую вокруг источника вектора односвязную поверхность S. скалярная и может быть представлена как
скалярная и может быть представлена как
 (4)
(4)
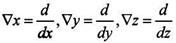

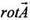 в цилиндрической координате имеет вид
в цилиндрической координате имеет вид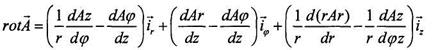


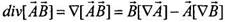




 -называют оператором Лапласа
-называют оператором Лапласа
 (8)
(8) (9)
(9) (10)
(10) (11)
(11)
 в пределе Sk®0, поскольку S конечна.
в пределе Sk®0, поскольку S конечна. через замкнутую поверхность S равен объемному интегралу от расхождения вектора
через замкнутую поверхность S равен объемному интегралу от расхождения вектора  (13)
(13)


