Решение неоднородных уравнений Максвелла, вектор Герца.
При решении уравнений Максвелла в общем случае находят значения полей Точка над означает, что эти поля изменяются по гармоническому закону. Однако зависимость полей от трех координат требует решения системы уравнений, что является весьма трудоёмким делом. На практике в ряде задач невозможно пренебречь значением плотности сторонних токов, что еще более усложняет задачу решения уравнений Максвелла для каждого конкретного случая, в частности задачи возбуждения волноводов, штырей, петель и т.д. Для задач такого рода можно пренебречь плотностью электрического заряда r=0. Система уравнений Максвелла при этом приобретает вид
Относительное значение диэлектрической постоянной
- векторная функция пространственных координат называют электрическим векторным потенциалом. Напряженность магнитного поля
Функция
поскольку из векторного анализа следует, что
Свяжем электрический векторный потенциал
или
Поскольку
справедливо равенство При этом сохраняется направление стрелок на силовых линиях электрического поля от + → - Таким образом, мы нашли способ выразить напряженность электрического и магнитных полей через векторный АЭ и скалярный электрические потенциалы j
(5)
Задача значительно упрощается, поскольку вместо двух векторов функций надо найти две функции — одну векторную и одну скалярную. Возможно использование всего одной векторной функции Предположим, что
Если наложить на функцию Следовательно для решения, например, неоднородного уравнения Гельмгольца
где
в общем случае, когда сторонними токам При этом следует заметить, что для частного случая, когда r =0 в третьем уравнении системы (1) неоднородное уравнение Гельмгольца справедливо и для вектора-потенциала
Переход от вектора Герца в уравнении (8) к полям
(10)
А для уравнения (9) переход к полям
|

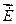 и
и 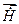 в зависимости от х, у, z в декартовой системе координат или от r, j, z в цилиндрической системе, при этом в электродинамике значение этих полей зависит от времени t. Эта зависимость может быть учтена предположением, что поля изменяются только по гармоническому закону и используя показательную функцию
в зависимости от х, у, z в декартовой системе координат или от r, j, z в цилиндрической системе, при этом в электродинамике значение этих полей зависит от времени t. Эта зависимость может быть учтена предположением, что поля изменяются только по гармоническому закону и используя показательную функцию  , где
, где  , а w - угловая частота, t - текущее время, можно производить все математические преобразования полей
, а w - угловая частота, t - текущее время, можно производить все математические преобразования полей  и
и 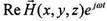

 (1)
(1) предполагаем величиной комплексной в общем случае найти все 6 проекций векторов
предполагаем величиной комплексной в общем случае найти все 6 проекций векторов  [2] Например, четвертому уравнению удовлетворяет векторное поле
[2] Например, четвертому уравнению удовлетворяет векторное поле
 (т.к.
(т.к.  ) (2)
) (2) будет равна:
будет равна: (3)
(3)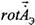 - неопределена, единственное условие налагаемое на функцию
- неопределена, единственное условие налагаемое на функцию  - это ее дифференцируемость. Равенства сохраняет силу, если к полю
- это ее дифференцируемость. Равенства сохраняет силу, если к полю 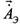 добавить еще одну функцию радиуса
добавить еще одну функцию радиуса 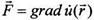 .
. - произвольная гладкая функция радиуса-вектора,
- произвольная гладкая функция радиуса-вектора,
 с напряженностью электрического поля. Подставим (3) во второе уравнение нашей системы (1)
с напряженностью электрического поля. Подставим (3) во второе уравнение нашей системы (1)
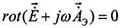 (4)
(4) ,то
,то  (5)
(5) - скалярный электрический потенциал (знак «-» поскольку должно быть
- скалярный электрический потенциал (знак «-» поскольку должно быть )
)

 , которая носит название вектор Герца[1].
, которая носит название вектор Герца[1]. (6)
(6) (7)
(7) и
и 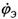 ограничение
ограничение  , которое носит название калибровка Лоренца, то можно убедиться, что условие калибровки Лоренца выполняется и для функции
, которое носит название калибровка Лоренца, то можно убедиться, что условие калибровки Лоренца выполняется и для функции  .
. (8)
(8)
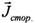 нельзя пренебречь.
нельзя пренебречь.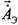 в виде
в виде (9)
(9) и
и  осуществляется посредством формул
осуществляется посредством формул

 посредством соотношений (5).
посредством соотношений (5).


