РАБОЧАЯ ПРОГРАММА, МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ДИСЦИПЛИНЕ
1. Выделение функционального компонента – нахождение уравнения линии регрессии 2. Оценка доли функционального компонента в стохастической зависимости: коэффициент корреляции r, если 1,2,3,4,5,6 4,6,5,1,3,2 2,1,6,5,4,3 и другие. ----------------------- По определению, инверсию образуют два числа в перестановке когда меньшее из них расположено правее большего. Каждой перестановке можно сопоставить число инверсий в ней, которое подсчитывается следующим образом: для каждого из чисел определяют количество стоящих правее его меньших чисел, и полученные результаты складываются.
Например, определим число инверсий в следующей перестановке: (5,3,1,4,2,6).
Решим задачу за пять шагов, на первом шаге выделим первый (слева направо) элемент и подсчитаем число элементов стоящих правее от него меньших чем он сам. (меньшие элементы будем зачеркивать). Затем аналогичным образом обработаем второй элемент и т.д.
Gt; 4 Gt; 2 Gt; 0 Gt; 1 Gt; 0
Итого, число инверсий в заданной перестановке составляет: 4 + 2 + 0 + 1 + 0 = 7
Перестановка называется четной, если число инверсий в ней четно, и нечетной - в противном случае. В частности, рассмотренная выше перестановка нечетная, так как количество инверсий в ней равно семь. ------------------------------------------------------------------------------- Транспозиции Транспозиция – элементарное преобразование строк/столбцов матрицы, заключающееся в перемене мест двух строк/столбцов матрицы, при этом позиции остальных элементов не меняется.
Отсюда вытекает одно из свойств определителя: - Определитель меняет знак при любой транспозиции его столбцов/строк. Это происходит из-за того, что транспозиция меняет чётность перестановки на противоположную. -------------------------------------------------------------------------------
Свойства определителей: -определитель транспонированной матрицы; -перемена строк местами в определителе; -определитель матрицы с одинаковыми строками 1). Транспонирование - замена строк на столбы в матрице. Примеры:
Из свойств транспонированной матрицы следует, что определитель транспонированной матрицы равен определителю исходной матрицы:
----------------------- 2). При перестановке мест строк/столбцов матрицы определитель меняет свой знак на противоположный, при этом абсолютное значение не меняется. (и пример на основе матриц выше)
ч 3). Определитель матрицы с 2-я одинаковыми строками = 0 Пусть A - квадратная матрица, имеющая две одинаковые строки/столбца. И пусть B - матрица полученная в результате перестановки указанных одинаковых строк/столбцов матрицы A.
С одной стороны det A = det B, но в силу свойства №2 следует, что det A = - det A, откуда следует что det A = 0. ------------------------------------------------------------------------------- Свойства определителей: -разложение определителя по строке Разложение определителя по строке - сумма произведений элементов какой–либо его строки на их алгебраические дополнения(минор умноженный на
Ликбез: i - номер строки j - номер столбца. Пример а12: i=1, j=2
Пример разложения по первой строке матрицы вида:
∆= или ∆=а11 ------------------------------------------------------------------------------- Свойства определителей: -произведение элементов одной строки на алгебраические дополнения другой строки; -умножение строки на число; -две пропорциональные строки; -разложение определителя на сумму двух; -прибавление к элементам одной строки элементов другой строки, умноженных на одно и то же число. 1). ----------------------- 2). При умножении элементов к-строки на одно и то же число, определитель умножается на это же число. (это число можно вынести за скобки матрицы и при нахождении определителя оно будет умножаться на определитель).(можно пример) ----------------------- 3). Если в матрице существуют 2 пропорциональные строки, то ее определитель равен 0 (коэффициент пропорциональности можно вынести за знак определителя, тогда матрица полученного определителя будет содержать две равные строки, откуда следует из свойства определителя матрицы с 2-мя одинаковыми строками, что det=0) ----------------------- 4). ----------------------- 5). -------------------------------------------------------------------------------
Определитель Вандермонда
Определитель Вандермонда равен нулю тогда и только тогда, когда существует хотя бы одна пара -------------------------------------------------------------------------------
Определитель ступенчатой матрицы ------------------------------------------------------------------------------- Теорема Лапласа Пусть выбраны любые k строк матрицы A. Тогда определитель матрицы A равен сумме всевозможных произведений миноров k-го порядка, расположенных в этих строках, на их алгебраические дополнения.
где суммирование ведётся по всевозможным номерам столбцов РАБОЧАЯ ПРОГРАММА, МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ДИСЦИПЛИНЕ
|

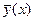 .
.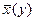 - прямые; корреляционные отношения
- прямые; корреляционные отношения 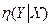 ,
, 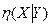 в общем случае.
в общем случае. и
и 
 (и пример на основе матриц выше)
(и пример на основе матриц выше)
 ).
).
 +
+  +
+ 
 - а12
- а12  + а13
+ а13 

 такая, что
такая, что  .
.




