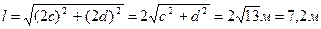Приклади розв'язування задач
Задача 1. На якій відстані один від одного необхідно підвісити лампи в теплицях, щоб освітленість Е на поверхні Землі в точці, що лежить посередині між двома лампами, була не менше 200 лк? Висота теплиці h = 2 м. Сила світла кожної лампи I = 800 кд (рис. 15). Розв'язування. Відстань l між лампами можна визначити з формули прямокутного трикутника:
Лампу можна прийняти за точкове джерело світла, оскільки її розміри малі в порівнянні з відстанню до точки, в якій визначається освітленість. Тому знайти відстань r від лампи до точки А можна з формули освітленості:
де
Підставимо вираз (3) в (1):
Підставимо числові значення величин в (4) і обчислимо
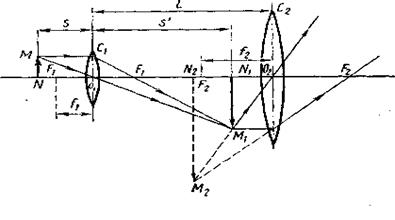
Задача 2. Фокусна відстань об'єктиву мікроскопа f1 =5 мм, окуляра f2=25 мм. Предмет знаходиться на відстані s==5,1 мм від об'єктиву (рис.16). Обчислити довжину тубуса мікроскопа і збільшення, що дається мікроскопом
Рис.16. Розв'язування. Збільшення мікроскопа
де
де s' — відстань від об'єктиву до дійсного зображення, що дається їм; 0,25 м — відстань якнайкращого бачення для нормального ока. З обліком (2) і (3) формула (1) прийме вигляд
Відстань s' від об'єктиву до зображення можна знайти з формули лінзи:
(s— відстань від предмету до лінзи), звідки Підставивши вираз для s' у (4), одержимо
Випишемо величини, що входять у формулу (5), в СІ: s = Довжину тубуса визначимо, виходячи з таких міркувань, Дійсне зображення, що дається об'єктивом, повинне лежати у фокусі окуляра, оскільки окуляр діє як лупа (мал. 10). Тому довжина тубуса
Підставимо числові значення величин в (5) і (6) і обчислимо:
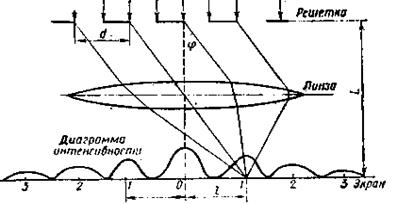
Задача 3. Визначити число штрихів на 1 мм дифракційних грат, якщо при нормальному падінні світла довжиною хвилі Розв'язування. Число штрихів N на 1 мм грат визначимо по формулі N =1/ d (1) де d — період грат (мал. 11). Період грат знайдемо з умови максимуму:
де Зважаючи на те що для максимуму 1-го порядку кут малий, можна прийняти
Підставивши у формулу (2) вираз синуса кута з (3),визначимо постійну грати:
З обліком (4) формула (1) прийме вигляд
Рис.17. Випишемо числові значення величин, що входять в (5), в СІ: l = 3,3м L=1,10 м k =1, Підставимо числові значення величин в (5) і обчислимо. Задача 4. Частота потужних імпульсів випромінювання радіолокатора аеропорту 500 Гц. Який радіус його дії? Як довго ціль, що рухається зі швидкістю 900 км/год, летітиме від краю зони спостереження до точки розташування радіолокатора? Розв'язання. Між двома імпульсами проходить час Таку відстань ціль пройде за час t = R/v = 20 хв. Відповідь: радіус дії локатора 300 км; таку відстань пасажирський літак проходить за 20 хв.
Розв’язання: На рис.18. пунктиром показано початкове положення дзеркала,суцільною лінією – його положення після повороту на кут
Відповідь: якщо екран знаходиться на відстані 19 000 – 38 000 км і далі, то швидкість «зайчика» від дзеркала дорівнює перевищить швидкість світла у вакуумі. Задача 6. У кімнаті площею дві суміжні стіни являють собою плоскі дзеркала. Яку площу кімнати бачить людина, яка стоїть на відстані 2м від одного і 3м — від другого дзеркала? Яка відстань від людини до найбільш віддаленого до неї зображення? Розв'язання. Будуючи зображення, переконуємось, що їх три і вони разом з предметом утворюють прямокутник зі сторонами 4м і 6м. Отже відстань від людини до найвіддаленішого її зображення
Очевидно, що людині кімната здається вчетверо більшою і має площу80 м2.
|

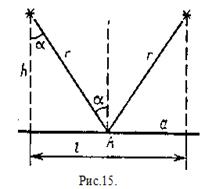
 (1)
(1)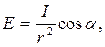 (2)
(2)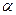 — кут, під яким падають промені. Підставивши в (2)
— кут, під яким падають промені. Підставивши в (2)  , виразимо r:
, виразимо r: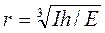 (3)
(3) (4)
(4)
 .
.
 (1)
(1)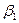 — збільшення об'єктиву;
— збільшення об'єктиву; 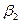 — збільшення окуляра, визначувані по формулах
— збільшення окуляра, визначувані по формулах
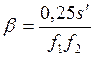 (4)
(4)

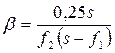 (5)
(5)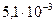 м f 1=
м f 1= 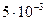 м, f 2 =
м, f 2 =  м.
м.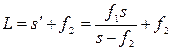 (6)
(6)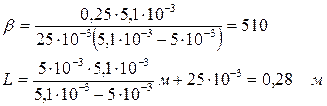
 =600 нм грати дають перший максимум на відстані l= 3,3 см від центрального. Відстань від грат до екрану L = 110см.
=600 нм грати дають перший максимум на відстані l= 3,3 см від центрального. Відстань від грат до екрану L = 110см.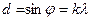 (2)
(2)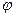 — кут, під яким спостерігається к-й максимум; к — порядок (номер) максимуму.
— кут, під яким спостерігається к-й максимум; к — порядок (номер) максимуму.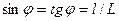 (3)
(3)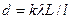 (4)
(4) (5)
(5)
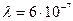 м.
м. . За цей час імпульс має дійти до цілі, відбитись і повернутись до приймача локатора. Отже, радіус дії
. За цей час імпульс має дійти до цілі, відбитись і повернутись до приймача локатора. Отже, радіус дії 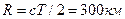 .
.
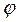 . Легко бачити, що перпендикуляр до дзеркала робить поворот на
. Легко бачити, що перпендикуляр до дзеркала робить поворот на 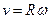 знаходимо відстань до екрану:
знаходимо відстань до екрану: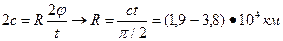 .
.