Задача 10. Яка може бути найменша відстань L між предметом і його зображенням у збірній лінзі з фокусною відстанню F?
Розв'язок:Може бути два випадки: 1) необхідно знайти відстань між предметом і дійсним зображенням (предмет і зображення знаходяться по різні боки від лінзи, рис.21); 2) необхідно знайти відстань між предметом і уявним зображенням (предмет і зображення знаходяться по один бік від лінзи, рис.21).
Рис.21 Нехай величини d і f (відстань від предмета до лінзи і від лінзи до зображення), які входять у формулу лінзи, є координатами предмета і зображення на числовій осі, яка збігається з оптичною віссю лінзи. При цьому за початок відліку оберемо оптичний центр лінзи, а додатний напрямок відліку нехай збігається з напрямком поширення світла. Тому відстань між предметом і зображенням, що буде відраховуватись вздовж цієї осі, є велечина додатна. Розглянемо перший випадок, коли предмет знаходиться на відстані d>F від лінзи. Запишемо формулу тонкої лінзи:
Оскільки, згідно з умовою задачі,
Тут L – функції двох змінних d і f. Тепер можна застосувати звичайний метод дослідження функції на екстремум. Необхідно взяти першу похідну від L по змінній f і прирівняти її до нуля:
Рівняння (3) має два корені: f=0 і f=2F. Для першого випадку, коли зображення дійсне, має виконуватись нерівність f>F, тому перший корінь не підходить. Отже, f=2F. Підставивши вираз для f у формулу (2), знайдемо мінімальну відстань L:
Якщо ж зображення уявне (другий випадок), то Це відповідає випадку, коли предмет знаходиться біля лінзи і зображення збігається з ним. Для того щоб впевнитись, що значення f відповідає мінімальному, а не максимальному значенню L, візьмемо другу похідну і визначимо її знак:
Знаки «+» і «-», які стоять перед дробом, відповідають нерівностям
Задача 11. Відстань від предмета до екрана. Лінза, яка розміщена між ними, дає чітке зображення предмета на екрані у двох положеннях, відстань між якими. Знайти фокусну відстань лінзи. Розв’язок:Побудуємо чіткий рисунок ходу променів, який відповідатиме умові задачі (рисунок 22).
Рис. 22 Оскільки зображення на екрані, то воно є дійсним, і відповідно лінза є збірною (рис.22). За умовою задачі Запишемо формулу тонкої лінзи і знайдемо відстань від лінзи до зображення Побудуємо графіки функцій Для побудови графіка функції
Зрозуміло, що для побудови графіка Графіки залежностей f(d) наведені на рисунку (23).
Рис.23 Пряма Ці точки можна знайти, якщо розв’язати рівняння
З цього можна зробити висновок, що обидва корені додатні. За умовою задачі
Розглянемо випадок, коли відстань між предметом і екраном залишається постійною, а переміщують тільки лінзу, тобто Розробимо два чітких рисунки (рис.24), які відповідають двом положенням лінзи, розмістивши їх один під одним.
Рис.24 Запишемо рівняння для такої лінзи щодо обох положень:
Порівнявши обидва рисунки і уважно прочитавши умову задачі, одержимо
Підставивши вирази для
Розв’яжемо цю систему відносно
Підставимо вирази
Задача 12. Точкове джерело світла розміщене на відстані від збірної лінзи з фокусною відстань. За першою лінзою розмістили розсіювальну лінзу, але так, що система дає дійсне зображення джерела з лінійним збільшенням на відстані від першої лінзи. Знайти положення розсіювальної лінзи та її фокусну відстань. Розв'язання. Зробимо чіткий схематичний рисунок (рис.25).
Рис.25 Побудуємо проміжне зображення точки S, не враховуючи наявності лінзи Запишемо формулу тонкої збірної лінзи і формулу для пошуку збільшення, яке дає лінза.
Побудуємо зображення точки
Рис. 26 Запишемо рівняння для тонкої розсіювальної лінзи:
Ми отримали чотири рівняння для системи лінз:
Розглянувши уважно рисунки 25 і 26, робимо висновок, що
Підставимо вирази для
За умовою задачі відомо, що збільшення k системи дорівнює одиниці, а оскільки Система рівнянь матиме вигляд
Оскільки за умовою задачі відомі
З рівняння (6) знайдемо
З рівняння (5) знайдемо фокусну відстань розсіювальної лінзи
Задача 13. На відстані d від тонкої збірної лінзи на головній оптичній осі розміщено джерело світла. За лінзою на відстані 0,75 d помістили плоске дзеркало (рис.27). Зображення знаходиться посередині відрізка, що з'єднує джерело з центром лінзи. Знайти фокусну відстань лінзи. Розв'язок: Запишемо формулу тонкої збірної лінзи
Зображення, яке дає лінза, розміщується в точці S1 на відстані f від лінзи. У зворотному напрямку, оскільки на відстані 0,75d розміщене дзеркало, предмет буде знаходитись в точці
Рис.27 З рисунка видно, що За умовою задачі
Ми отримали систему рівнянь (рівняння (1)-(3)):
Розв’язавши цю систему рівнянь відносно F, дістанемо
Отже, Отже, фокусна відстань розсіювальної лінзи
|


 (1)
(1) , то, підставивши вираз для визначення d в рівняння (16.15) і рзв’язавши його відносно L отримаємо
, то, підставивши вираз для визначення d в рівняння (16.15) і рзв’язавши його відносно L отримаємо (2)
(2) ,
, . (3)
. (3) .
.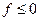 ; тоді використаємо перший корінь, коли
; тоді використаємо перший корінь, коли  . Отже,
. Отже, 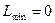 .
. .
. і
і  , тому в будь-якому випадку
, тому в будь-якому випадку  і відповідно виконується умова мінімуму функції
і відповідно виконується умова мінімуму функції  .
.
 – висота предмета,
– висота предмета, 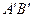 - висота зображення,
- висота зображення, 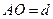 -відстань від предмета до оптичного центра лінзи,
-відстань від предмета до оптичного центра лінзи,  - відстань від оптичного центра лінзи до зображення.
- відстань від оптичного центра лінзи до зображення. .
. .
. і
і  .
. .
.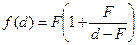 спочатку необхідно побудувати графік 1/d, зсунути його на відстань F вправо по осі абсцис, помножити на F, зсунути на 1 по осі ординат і помножити на F.
спочатку необхідно побудувати графік 1/d, зсунути його на відстань F вправо по осі абсцис, помножити на F, зсунути на 1 по осі ординат і помножити на F.
 Прирівнявши праві частини цих рівнянь, дістанемо
Прирівнявши праві частини цих рівнянь, дістанемо  або
або 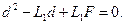 Розв’язавши квадратне рівняння відносно d, отримаємо
Розв’язавши квадратне рівняння відносно d, отримаємо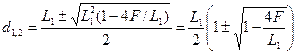 .
. , тоді
, тоді


 (1)
(1) . (2)
. (2)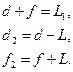
 і
і  в рівняння (2), отримаємо систему рівнянь
в рівняння (2), отримаємо систему рівнянь
 і
і  :
:


 . Проведемо довільний промінь AB (джерело світла розміщено в точці A). Щоб знайти хід променя AB після заломлення на лінзі, проведемо побічну оптичну вісь, яка буде паралельною до променя AB, і фокальну площину, що проходить через правий фокус збірної лінзи. Після заломлення промінь проходить через точку С (точку перетину фокальної площини і побічної оптичної осі). Зображення, яке дає лінза
. Проведемо довільний промінь AB (джерело світла розміщено в точці A). Щоб знайти хід променя AB після заломлення на лінзі, проведемо побічну оптичну вісь, яка буде паралельною до променя AB, і фокальну площину, що проходить через правий фокус збірної лінзи. Після заломлення промінь проходить через точку С (точку перетину фокальної площини і побічної оптичної осі). Зображення, яке дає лінза 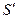 , буде на перетині променя BC і с головної оптичної осі.
, буде на перетині променя BC і с головної оптичної осі. (1)
(1)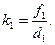 (2)
(2)
 (3)
(3)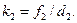 (4)
(4)


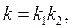 то
то 
 (5)
(5) (6)
(6) і
і  , то з рівняння (3) знаходимо
, то з рівняння (3) знаходимо
 :
:


 (1)
(1) на відстані
на відстані 
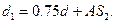 Оскільки
Оскільки  то
то  (2)
(2) Запишемо формулу лінзи для того випадку, коли промінь проходитиме лінзу в зворотньому напрямку з точки
Запишемо формулу лінзи для того випадку, коли промінь проходитиме лінзу в зворотньому напрямку з точки  (3)
(3)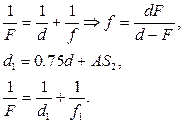
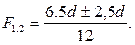
 Перше значення кореня
Перше значення кореня  не підходить за умовою задачі, оскільки
не підходить за умовою задачі, оскільки 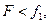 а
а  значить
значить 




