Имена в формулах

Использование имен в формулах облегчает понимание расчетов, которые они выполняют. Например, формулы:

=СУММА(Продано_в_сентябре) или =скорость*время

воспринимаются значительно легче, чем:

=СУММА(C20:C30) или =A10*B10.

Рис. 4. Группа Определенные имена вкладки Формулы Ленты

Поименованными могут быть ячейки, диапазоны (смежные и несмежные), строки и столбцы, а также константы, формулы и таблицы. Имена ячеек и диапазонов являются абсолютными ссылками. Для работы с именами используются элементы управления, расположенные в группе Определенные имена вкладки Формулы Ленты (рис. 4).

Чтобы задать имена отдельным ячейкам, диапазонам, строкам или столбцам достаточно выделить нужную часть электронной таблицы, а затем задать для нее имя в поле Имя строки формул, не забыв завершить ввод нажатием клавиши Enter.

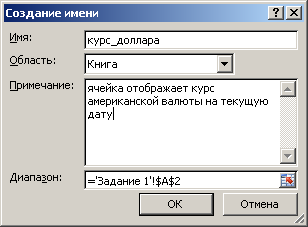
Больше возможностей дает диалоговое окно Создание имени, которое открывается кнопкой Присвоить имя из раздела Определенные имена вкладки Формулы Ленты (рис. 5).

Рис. 5. Диалоговое окно Создание имени

Для управления именами используется диалоговое окно Диспетчер имен, которое открывается одноименной кнопкой, расположенной в разделе Определенные имена вкладки Формулы Ленты.

Рис. 6. Ввод имен в формулы с помощью списка Использовать в формуле

При создании формул в них можно использовать существующие в книге имена ячеек, диапазонов, констант, формул и таблиц. Это можно сделать, набирая имена с клавиатуры. Но гораздо легче в процессе создания формулы выбирать имена из списка имен, который открывается кнопкой Использовать в формуле из группы Определенные имена вкладки Формулы Ленты (рис. 6).