РАЗДЕЛ 3
УРАВНЕНИЕ БЕРНУЛЛИ
Количество жидкости, проходящее через живое сечение (ЖС) в единицу времени, называют расходом. Различают расходы: · объемный
· массовый
· весовой
На пути движения жидкости (рис.3.1) конфигурация потока и поле скоростей в его живом сечении (ЖС) могут изменяться, но количество жидкости, прошедшее за время t через любое сечение, неизменно, это фиксируется уравнением неразрывности:
Для капельной жидкости ее плотность r мало зависит от величины давления р (по крайней мере, при изменении р в пределах 10 МПа). При r = const выражение (3.4) будет соответствовать закону постоянства объемного расхода на рассматриваемом участке потока:
Для газа плотность r зависит от давления р и температуры T, поэтому при расчете газопроводов используют зависимости (3.4) и (3.2), при этом
где R – газовая постоянная, для воздуха Полный запас энергии Е некоторого объема жидкости массой m относительно произвольной горизонтальной плоскости сравнения определяется выражением
где mgz = Ez – потенциальная энергия положения, Дж; z – вертикальная координата точки или тела (z положительна, если тело расположено выше плоскости сравнения, и отрицательна – если ниже); Энергия, отнесенная к массе m, объему V или весу G, называется удельной энергией. Так, энергия, приходящаяся на единицу массы,
Энергию, приходящуюся на единицу объема (т.е. давление), получим, разделив выражение (3.7) на V; при этом
Энергию, приходящуюся на единицу веса (т.е. напор), получим, разделив (3.7) на G; при этом G = mg,
Связь между давлением р и напором Н выражается согласно выражению (2.3) формулой р = r gH. (3.11) При движении реальной жидкости (r = const, m > 0) кинетическая энергия в сечении потока может распределяться по-разному в зависимости от режима движения и вида потока. Так, при ламинарном режиме эпюра скоростей в ЖС – парабола, при равномерном установившемся турбулентном движении эта эпюра напоминает трапецию, для струи – прямоугольник, т.е. степень равномерности распределения кинетической энергии в ЖС потока для разных условий различна. Это отражается через коэффициент Кориолиса, который вводят в состав кинетической энергии в формулах (3.8)-(3.10) как множитель a. Для Re < 2320 a = 2; для Re > 2320 при равномерном движении турбулентного потока a = 1,03-1,10. С целью упрощения расчетов в последнем случае рекомендуется принимать a» 1. Для струи и идеальной жидкости a = 1. В сечении 1-1 полная энергия (рис.3.1)
в сечении 2-2
потерянная между сечениями 1-1 и 2-2 часть энергии составит
Здесь закон сохранения энергии имеет вид
или
Уравнение (3.12) есть уравнение Бернулли для реального потока капельной жидкости. Потери энергии (напора) по длине потока определяются формулой Дарси
где l – коэффициент гидравлического трения (или коэффициент Дарси). Участок потока, где скорость изменяет свое направление и значение, называют местным сопротивлением (МС). Протяженность МС мала по сравнению с длиной прямых участков, поэтому считают, что МС длины не имеет. Эти потери определяются по формуле Вейсбаха:
где z – коэффициент местного сопротивления. Коэффициент Дарси в общем случае зависит от режима движения (Re) и шероховатости (D) твердых границ потока, т.е.
Число Рейнольдса Re (безразмерное) характиризует соотношение сил инерции (через среднюю скорость v) и сил вязкого трения (через кинематический коэффициент вязкости n)
где Для ЖС круглой формы диаметром d L = d; для ЖС некруглой формы L = 4 R г; R г – гидравлический радиус,
где S ЖС – площадь живого сечения, м2; c – смоченный периметр, м. Смоченный периметр – это длина линии контакта жидкости с твердыми стенками в ЖС (длина свободной поверхности жидкости в смоченный периметр не входит). Для ламинарного режима движения (линейная зона сопротивления, 0 < Re < 2320 и Для общего случая турбулентного режима (Re > 2320) по А.Д.Альтшулю
где Δэ – эквивалентная (зернистая) шероховатость, мм. Турбулентный режим подразделяют на три зоны сопротивления, границы между которыми ориентировочно соответствуют: · зоне гладкого трения или зоне гидравлически гладких труб, когда толщина δ ламинарного пристенного слоя больше высоты Δ (или Δэ) шероховатостей, т.е. δ > Δ. При этом lII ≠ f (Δ). Эта зона соответствует
· зоне гидравлически шероховатых труб, когда δ ≤ Δ. При этом ядро потока дополнительно турбулизируется, касаясь выступов шероховатости, и lIII = f (Re, Δ). Эта зона примерно соответствует
· квадратичной зоне сопротивления (
В справочниках приводятся значения l для квадратичной зоны сопротивления. В табл.3.1 даны значения эквивалентной шероховатости для некоторых видов труб [1, 5].
Таблица 3.1
Коэффициенты местных сопротивлений z в общем случае зависят от режима движения (Re), расстояния между двумя МС (L), степени открытия запорного устройства и от вида МС. В квадратичной зоне сопротивления При ламинарном движении нужно учитывать поправку В к формуле (3.14), которая для потерь давления будет иметь вид:
где указанная поправка может быть ориентировочно определена из следующих данных [10]:
Все справочные данные приводятся для одиночного МС, к которому жидкость подходит с неискаженной эпюрой скоростей u. К таким эпюрам относится парабола (ламинарный режим; a = 2,
где J – гидравлический уклон,
D hl и D pl – потери соответственно напора и давления по длине потока l; ν – кинематический коэффициент вязкости, м2/с; r – радиус трубы, м; y – текущая координата для рассматриваемого слоя жидкости. Любое МС искажает поле скоростей. Если между двумя смежными МС расстояние L недостаточно для восстановления нарушенной эпюры, то к МС № 2 поток подойдет с искаженной эпюрой, и коэффициент z2 не будет соответствовать указанному в справочнике или полученному расчетом. По опытным данным общий коэффициент нескольких близко расположенных МС бывает меньше арифметической суммы отдельных z, присущих этим МС, т.е. Базовой длиной между двумя МС, достаточной для выравнивания поля скоростей, считают
Расчетным путем можно определить потери энергии: · от внезапного расширения потока от сечения S 1 до сечения S 2 > S 1
при S 2 >> S 1 (выход потока из трубы в резервуар с v» 0) · от внезапного сужения потока от сечения S 1 до сечения S 2 < S 1
при S 1 >> S 2 (вход в трубу из резервуара)
Данные о z при сочленении двух плавных колен приведены на рис.3.2 [1]. Коэффициент сопротивления диафрагмы ζд, расположенной внутри трубы постоянного сечения (рис.3.3),
где
Коэффициент сопротивления сварного стыка на трубопроводе
где δ – высота сварного стыка (шва), выступающего внутрь трубы; d – внутренний диаметр трубы. Возрастание гидравлического сопротивления, вызванное сварными швами, определяется формулой
где l1, l – сопротивление трубопровода, соответственно, с учетом и без учета сварных швов; l – расстояние между стыками (длина труб).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Пример 3.1. Определить направление движения реальной жидкости и вид местного сопротивления в наклонном трубопроводе при следующих исходных данных: геодезическая отметка сечений z 1 = 2 м, z 2 = 6 м; манометрическое давление p 1 = 0,1 МПа, p 2 = 0,05 МПа; диаметры трубопровода d 1 = 200 мм, d 2 = 120 мм; расход жидкости кинематический коэффициент вязкости жидкости Решение. Жидкость должна двигаться от области с большей полной удельной энергией в область с меньшей энергией. Полная удельная энергия в сечении 1-1 и 2-2 согласно (3.12):
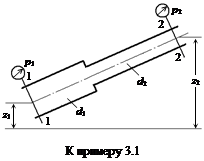
Жидкость движется от сечения 1-1 к сечению 2-2, если Е 1 > Е 2, и наоборот. Для определения Е 1 и Е 2 нужны сведения о средних скоростях v 1 и v 2, коэффициентах Кориолиса a1 и a2 и плотности r. Используя формулу расхода (3.5), имеем
Коэффициент Кориолиса зависит от режима движения и вида потока. В задаче поток напорный, т.е. для круглого сечения
Заданному ν согласно табл.1.1 соответствует жидкость из группы минеральных масел При этом:
Так как Е 1 > Е 2, масло движется от сечения 1-1 к сечению 2-2, а местное сопротивление называется внезапным сужением потока.
Пример 3.2. Вода для поливки улиц поступает из накопителя в цистерну емкостью V = 10 м3 за время t по трубопроводу диаметром (условный проход) d = 50 мм и длиной l = 10 м. На трубопроводе имеется регулируемый пробковый кран с коэффициентом местного сопротивления zкр. При zкр = 40 цистерна наполняется за t 1 = 1 ч. На какой угол β надо установить рукоятку крана, чтобы вдвое сократить время наполнения цистерны (t 2 = 0,5 ч)? Принять для трубопровода трубу стальную тянутую, новую; высотой h пренебречь. Уровень воды в накопителе за время заправки цистерны постоянен. Данные для решения:
Решение. Составим уравнение Бернулли по типу (3.12), включающее данные о потерях в местных сопротивлениях. С этой целью проведем плоскость сравнения 0-0 по оси трубы, зададим начальное сечение 1-1 по свободной поверхности воды в накопителе, а сечение 2-2 на выходе из трубы. Тогда:
где z 1 = H; z 2 = 0; р 1 = р 2 = р а; v 1» 0; После подстановки названных величин имеем:
Для решения этого уравнения необходимо иметь сведения о средней скорости v 2, коэффициенте Кориолиса a2 и коэффициенте Дарси l. Обозначим v 2 через v. Согласно (3.1)
Определим режим движения, приняв для воды
т.е. режим турбулентный и a» 1. Уточним зону сопротивления. Для указанных в задании труб шероховатость Δэ = 0,015 мм (табл.3.1). Тогда
Находим напор в накопителе:
Выразим новое значение
где v нов – новая средняя скорость в трубе, При этом Полученное Re также относится к третьей области сопротивления:
т.е.
Согласно данным для решения в условии примера на приведенном рисунке zкр = 4,45 соответствует примерно углу установки крана β» 26о. Так как начальная величина zкр = 40 соответствовала b» 45о, кран следует приоткрыть. Заметим, что изменение угла b примерно в 1,7 раза вызвало изменение сопротивления крана примерно в 9 раз и сократило время заправки цистерны в 2 раза.
ЗАДАЧИ
Задача 3.1. Жидкость перетекает при H = const из резервуара N в резервуар M по трубопроводу, состоящему из двух участков ( Определить расход жидкости Q при Н = 1 м и h 1 = 0,25 м. Ответ: Q = 2,2 л/с.
Задача 3.2. Жидкость перетекает из бака N в бак М по трубопроводу, состоящему из двух прямых отрезков ( 1. Определить расход жидкости Q. 2. Построить напорную линию (НЛ) и пьезометрическую (ПЛ) от бака N до бака М. Ответ: Q = 18 л/с.
Задача 3.3. Из реки в колодец с расходом Q = 10 л/c поступает вода через приемный фильтр (zф = 12) и трубопровод ( По достижении разности уровней воды в реке и колодце Н автоматически включается насос, подающий воду с тем же расходом на производственные нужды. Определить величину Н.
Ответ: Н = 3,34 м.
Задача 3.4. Из большого резервуара вода подводится к пункту потребления под напором Н по горизонтальному трубопроводу общей длиной Определить напор Н, если пропускная способность трубопровода Q = 0,05 м3/с; принять коэффициент Дарси l = 0,025. Построить для трубопровода напорную линию (НЛ) и пьезометрическую (ПЛ). Ответ: Н = 6,8 м. Задача 3.5. В нижнем баке существует манометрическое давление р м над свободной поверхностью воды. Под действием этого давления вода с расходом Q транспортируется по вертикальному трубопроводу в верхний открытый бак. Дано: d = 0,025 м, Определить р м. Ответ:
Задача 3.6. Центробежный насос (ЦН) забирает воду из колодца по всасывающей трубе (ВТ) длиной L 1 = 12 м через приемный клапан с сеткой (zф1 = 6).
Колодец сообщается с большим водоемом самотечной трубой (СТ) с сеткой (zф2 = 2); длина СТ L 2 = 20 м. Расход ЦН и пропускная способность СТ одинаковы. Определить расход Q и разность уровней воды в водоеме и колодце Z, если d 1 = d 2 = d = 150 мм, допустимая вакуумметрическая высота ЦН [ Н вак] = 6 м, коэффициент Дарси для ВТ и СТ одинаков (l = 0,03), а ось ЦН расположена выше уровня воды в водоеме (h = 2 м). Ответ: Q = 38 л/с; Z = 1,9 м.
Задача 3.7. Определить расход воды Q, истекающей из конического насадка в атмосферу, если в герметичном резервуаре большой емкости уровень воды постоянен и составляет Н = 5 м, а на свободной поверхности в резервуаре имеет место избыточное давление р = 0,4 МПа. Размеры трубопровода: Принять коэффициенты Дарси l1 = 0,043; l2 = 0,034 и коэффициенты местных сопротивлений: вентиля zв = 4, насадка zн = 0,06. Сжатием струи на выходе из насадка пренебречь; учесть другие
Ответ: Q = 68,2 л/с.
Задача 3.8. Вода вытекает в атмосферу по горизонтальной трубе, на которой установлены два пьезометра. Диаметр трубы d = 50 мм, длина каждого из трех участков l = 4 м, разность показаний пьезометров Δ h = 0,3 м. Определить расход Q и напор в резервуаре Н. Принять шероховатость трубы Δэ = 0,5 мм и кинематическую вязкость воды ν = 1 Ст; местными сопротивлениями пренебречь. Ответ: Q = 2,85 л/с, Н = 0,9 м.
Задача 3.9. Определить режим безнапорного движения воды (число Рейнольдса) в прямоугольном лотке шириной b = 80 см при высоте слоя воды в нем h = 38 см, если расход составляет Q = 5,5 м3/ч, а температура воды t = 10°С. Ответ:Re = 3004.
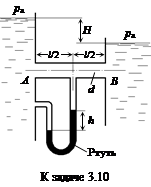
Задача 3.10. Определить расход воды Q, протекающей из бака А в бак В, и располагаемый напор Н, если показание ртутного дифманометра, присоединенного одним коленом к баку А, а другим – к середине трубы, составляет h = 440 мм.
Длина трубы l = 10 м, диаметр трубы d = 25 мм, ее шероховатость Δэ = 0,2 мм. Местные сопротивления учесть. Ответ: Q = 1,8 л/с, Н» 10,1 м.
Задача 3.11. Из накопителя А с постоянным уровнем периодически и кратковременно выпускают часть воды по самотечному трубопроводу с расходом Q = 126 м3/ч. Трубопровод стальной, эксплуатируется несколько лет и имеет следующие размеры: · верхний горизонтальный участок с шиберной задвижкой (ЗШ) – l 1 = 10 м, d 1 = 100 мм; · вертикальный участок – l 2 = 5 м, d 2 = d 1; · нижний горизонтальный участок – l 3 = 30 м, d 3 = 150 мм. Выпуск воды производят при полностью открытой ЗШ. Резерв высоты h в накопителе для твердого осадка равен 0,27 м; участки соединены между собой прямыми коленами с a = 90°. Определить высоту Н слоя воды в накопителе во время выпуска. Определение зоны сопротивления обязательно. Ответ: Н» 2 м.
Задача 3.12. Вода при температуре t = 10° С вытекает по горизонтальному трубопроводу в атмосферу при постоянном напоре Н = 1,8 м. Определить расход воды Q, если: · внутренний диаметр трубы d = 6,2 см; · задвижка шиберная (ЗШ) полностью открыта; · труба стальная, бывшая в употреблении;
· длина трубопровода l = 10 м. Ответ: Q = 7,24×10-3 м3/с. Задача 3.13. По наклонной прямой трубе длиной L = 2 км постоянного диаметра d = 100 мм перекачивают нефть (ρ = 950 кг/м3, n = 25×10-6 м2/с) с расходом Q = 5 л/с. Избыточное давление в начале трубы р 1 = 0,3 МПа. Определить угол a наклона трубы к горизонту, если в конце трубы давление атмосферное. Изобразить трубу по итогам расчета. Ответ:a = 24¢.
Задача 3.14. По трубе внутренним диаметром d = 100 мм перекачивают нефть плотностью Определить суточную пропускную способность трубы (массовый расход Q т). Ответ: Q т = 641,6 т/сут.
Задача 3.15. Определить часовой расход Q воды при ее движении безнапорно по желобу прямоугольной формы (ширина желоба а = 40 см, высота слоя воды h = 18 см) с числом Рейнольдса Re = 20000. Ответ: Q = 13,7 м3/ч.
Задача 3.16. Горизонтальная труба диаметром d 1 = 20 см в сечении а-а резко переходит в трубу диаметром d 2 = 10 см. Пренебрегая сопротивлениями и считая режим движения жидкости турбулентным, определить разность Δ h 1 уровней жидкости в пьезометрах, если в широком сечении жидкость движется со средней скоростью v = 0,8 м/с. Как изменится Δ h, если учесть местное сопротивление (резкое сужение)? Ответ:Δ h 1» 0,49 м; Δ h 2 = 0,685 м.
Задача 3.17. Определить манометрическое давление в сечении 1-1 (р 1) трубопровода, по которому движется жидкость плотностью r = 880 кг/м3, если средняя скорость в сечении 1-1 v 1 = 1,1 м/с и площадь живого сечения 2-2 (S 2) в 2,5 раза меньше S 1. Расчеты выполнить для двух случаев, показанных на рисунке. Принять манометрическое давление в сечении 2-2 р 2 = 2×105 Па, разность геодезических отметок сечений Δ Z = 8,7 м, жидкость считать идеальной. Ответ: р 1 = 2,78×105 Па (рисунок, а); р 1 = 1,28×105 Па (рисунок, б).
Задача 3.18. Определить среднюю скорость движения воды в сечении 2-2 v 2, если v 1 = 1,2 м/с, манометрическое давление р 1 = 1,2 кгс/см2 и р 2 = 1,1 кгс/см2, а разность геодезических отметок сечений 1-1 и 2-2 составляет Δ Z = 3 м.
Принять режим движения турбулентным, потери напора на преодоление всех гидравлических сопротивлений между сечениями 1-1 и 2-2 ΣΔ h 1-2 = 1,4 м. Ответ: v 2 = 7,25 м/с.
Задача 3.19. Пожарный рукав диаметром d 1 = 76 мм заканчивается коническим сходящимся насадком (брандспойтом), суммарные потери напора в котором составляют Δ h = 0,3 м при расходе Q = 8×10-3 м3/с.
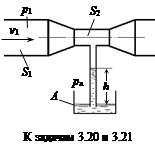
Определить манометрическое давление р 1 на входе в насадок, если струя воды поднялась на высоту Н = 26 м. Сопротивлением воздуха пренебречь. Ответ: р 1 = 2,57×105 Па. Задача 3.20. На какую высоту h может подняться вода из открытого резервуара А по трубке, присоединенной к узкому сечению S 2 трубопровода, если средняя скорость воды в широком сечении v 1 = 1,2 м/с, а манометрическое давление р 1 = 12000 Па? При этом площадь широкого сечения S 1 в пять раз больше S 2. Потерями энергии пренебречь. Ответ: h = 0,538 м.
Задача 3.21. По трубопроводу, имеющему сужение, движется вода с расходом Q = 22 л/с. Диаметр трубопровода в широком сечении d 1 = 200 мм, манометрическое давление там же р 1 = 12000 Па. Каким должен быть диаметр d 2 узкой части трубопровода, чтобы обеспечить подъем воды из открытого резервуара А на высоту h = 3,1 м? Потерями напора пренебречь. Ответ d 2» 55,1 мм.
Задача 3.22. По трубопроводу постоянного сечения длиной L = 56,4 км перекачивают нефть плотностью r = 860 кг/м3. Начальная отметка трубопровода выше конечной на 120 м. Определить величину гидравлического уклона I, если манометрическое давление в начале трубопровода р 1 = 3×106 Па, а в конце – атмосферное р 2 = р а. Ответ: I = 0,0084.
Задача 3.23. Определить манометрическое давление р 2 в точке 2 водопровода постоянного диаметра, имеющего общую длину L 1-2 = 12 км и L 2-3 = 4,2 км, если в точке 3 давление р 3 = р а, а в точке 1 манометрическое давление р 1 = 1,5 МПа. Геодезические отметки точек: z 1 = 0, z 2 = 64 м, z 3 = 42 м. Ответ: р 2 = 0,165 МПа.
Задача 3.24. Водомер Вентури имеет диаметры d 1 = 200 мм, d 2 = 100 мм. Определить расход воды Q, если показание ртутного дифманометра соответствует Δ h = 4,2 см. Принять коэффициент Кориолиса a = 1,06 и коэффициент расхода, учитывающий потери энергии в водомере m = 0,96. Ответ: Q» 24,4×10-3 м3/с. Задача 3.25. На горизонтальном участке трубопровода внутренним диаметром d 1 = 100 мм установлен водомер Вентури с диаметром суженной части d 2 = 50 мм. Определить, пренебрегая потерями энергии, расход воды Q по показанию ртутного дифманометра Δ h = 3,8 см, подключенного к широкому и узкому сечению водомера.
Установить область сопротивления широкого и узкого участков водомера, если эквивалентная шероховатость Δэ = 0,1 мм. Ответ: Q = 6,03 л/с.
Задача 3.26. По трубопроводу диаметром d 1 = 200 мм с резким сужением до диаметра d 2 = 100 мм перекачивают масло плотностью rм = 750 кг/м3. Избыточное давление в широкой трубе р 1 = 176,6 кПа, а в узкой трубе р 2 = 147,2 кПа. Геодезическая отметка первого сечения относительно второго z 1 = +1 м. Определить потери напора Δ h 1-2 на участке 1-2 при расходе масла Q = 31,4×10-3 м3/с. Определить полную энергию потока в первом сечении (гидродинамический напор) Н гд и кинетическую Hv. Ответ:Δ h 1-2 = 3,76 м; Н гд = 22,23 м; Hv = 0,051 м.
Задача 3.27. Трубопровод, имеющий в сечении 1 диаметр d 1 = 150 мм, постепенно расширяется до диаметра d 2 = 400 мм в сечении 2. Центр тяжести сечения 2 расположен выше центра тяжести сечения 1 на величину z 2 = 2 м. Определить разность полных напоров (Н 1 – Н 2) между сечениями 1 и 2, если расход воды по трубопроводу составляет Q = 106 л/с, а потери энергии на трение равны 20 % от потерь при внезапном расширении потока. Ответ: Н 1 – Н 2 = 0,472 м.
Задача 3.28. По прямому трубопроводу постоянного диаметра d = 250 мм, с шероховатостью Δэ = 0,04 мм, длиной l = 250 м, наклоненному к горизонту под углом a = 0°55¢, подается вода с расходом Q = 49,1×10-3 м3/с. Определить: · давление воды р 2 в сечении 2, если давление в сечении 1 составляет р 1 = 196,2 кПа, а жидкость движется от сечения 1 к сечению 2; · давление р 2 при р 1 = = 196,2 кПа, если жидкость движется от сечения 2 к сечению 1. При расчетах проверка области сопротивления обязательна. Ответ: р 2 = 149031 Па; р 2 = 164889 Па.
Задача 3.29. Вертикальная коническая труба длиной l = 4 м имеет нижний диаметр d 1 = 500 мм и верхний d 2 = 100 мм; из сечения 2-2 жидкость истекает в атмосферу со скоростью v 2 = 10 м/с.
Определить: · избыточное давление на входе воды в трубу р 1; · полную удельную энергию потока (с учетом атмосферного давления р а) на входе в трубу Н гд.1 и на выходе Н гд.2 относительно плоскости сравнения, проведенной через сечение 1-1. Ответ: р 1 = 93084 Па; Н гд.1 = 19,5 м; Н гд.2 = 19,1 м.
Задача 3.30. Определить гидравлический уклон I для напорного потока воды в трубе постоянного диаметра d = 0,1 м при расходе Q = 5×10-3 м3/с, если эквивалентная шероховатость трубы Δэ = 0,02 мм. Ответ: I = 0,0043.
Задача 3.31. По новому трубопроводу постоянного диаметра d = 200 мм длиной l = 1,6 км перекачивают в сутки 2794 т тяжелой нефти (r = 924 кг/м3, ν = 1,4 Ст). Определить потери напора Δ h по длине трубопровода, если он выполнен из стальных бесшовных труб. Ответ: Δ h» 8,36 м.
Задача 3.32. Определить допустимую высоту установки центробежного насоса над уровнем воды в колодце z н при следующих данных: вакуумметрическая высота всасывания насоса h вак = 4,8 м; диаметр всасывающей трубы d = 200 мм, ее длина l = 16 м; подача насоса Q = 173 м3/ч. На всасывающем трубопроводе имеются местные сопротивления: фильтрующая сетка с обратным клапаном zс и два плавных колена (zк) с поворотом на 90° и радиусом закругления R = 200 мм. При расчетах установление области сопротивления обязательно. Эквивалентную шероховатость трубы принять Δэ = 0,1 мм. Ответ:zн < 3,9 м.
Задача 3.33. Определить диаметр нефтепровода d и режим движения Re нефти (r = 885 кг/м3, ν = 0,25 Ст), если скорость ее движения Ответ: d = 158 мм; Re» 7600.
Задача 3.34. Из накопителя А в водоем В вода подается при температуре t = 30° С по сифонному трубопроводу с расходом Q = 50 л/с при разности уровней в водо
|

 м3/с; (3.1)
м3/с; (3.1) кг/с; (3.2)
кг/с; (3.2) Н/с. (3.3)
Н/с. (3.3) (3.4)
(3.4) . (3.5)
. (3.5)
 , (3.6)
, (3.6) ; Т – абсолютная температура, К; р – давление.
; Т – абсолютная температура, К; р – давление. (3.7)
(3.7) – потенциальная энергия давления, Дж;
– потенциальная энергия давления, Дж;  – кинетическая энергия, Дж.
– кинетическая энергия, Дж. Дж/кг. (3.8)
Дж/кг. (3.8) ,
, Дж/м3 = Па. (3.9)
Дж/м3 = Па. (3.9) Дж/Н = м. (3.10)
Дж/Н = м. (3.10)



 . (3.12)
. (3.12) (3.13)
(3.13) (3.14)
(3.14) . (3.15)
. (3.15) (3.16)
(3.16) ; L – характерный размер ЖС.
; L – характерный размер ЖС.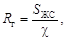 (3.17)
(3.17) )
)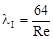 . (3.18)
. (3.18)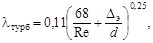 (3.19)
(3.19) , а коэффициент l может быть определен по Блазиусу
, а коэффициент l может быть определен по Блазиусу ; (3.20)
; (3.20) (3.19)
(3.19) ), когда δ → 0, а
), когда δ → 0, а  и не зависит от скорости потока v. Эта зона соответствует
и не зависит от скорости потока v. Эта зона соответствует  и по Шифринсону
и по Шифринсону (3.21)
(3.21) . Справочники приводят сведения о z именно для этой зоны.
. Справочники приводят сведения о z именно для этой зоны.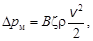 (3.22)
(3.22) ), описываемая формулой
), описываемая формулой , (3.23)
, (3.23) ; (3.24)
; (3.24) [9].
[9]. (3.25)
(3.25) (3.26)
(3.26)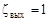 ;
; (3.27)
(3.27) .
.
 (3.28)
(3.28) ; εд – коэффициент сжатия струи (по А.Д.Альтшулю [5]),
; εд – коэффициент сжатия струи (по А.Д.Альтшулю [5]), (3.29)
(3.29)
 (3.30)
(3.30) (3.37)
(3.37)
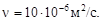



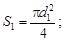


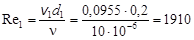 – ламинарный режим; a = 2;
– ламинарный режим; a = 2; – турбулентный режим; a» 1.
– турбулентный режим; a» 1. . Для более точного установления r можно воспользоваться справочными данными, например [1, с.314], жидкости с
. Для более точного установления r можно воспользоваться справочными данными, например [1, с.314], жидкости с  соответствует масло АМГ-10,
соответствует масло АМГ-10, 



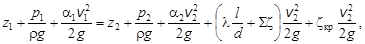
 ;
;  – для прямого колена с a = 90° [1].
– для прямого колена с a = 90° [1].

 (см. табл.1.5),
(см. табл.1.5),

 и
и  т.е. Re = 70750 относится к третьей зоне сопротивления, где l определяется формулой Альтшуля
т.е. Re = 70750 относится к третьей зоне сопротивления, где l определяется формулой Альтшуля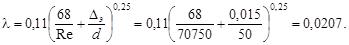

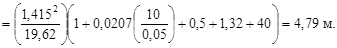



 aнов» 1.
aнов» 1. ,
,

 ,
, 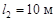 ) разного диаметра (d 1 = 50 мм, d 2 = 100 мм), при одинаковом коэффициенте Дарси (l1 = l2 = 0,03). На трубопроводе имеются два плавных колена (zк = 0,15) и внезапное расширение (zвр).
) разного диаметра (d 1 = 50 мм, d 2 = 100 мм), при одинаковом коэффициенте Дарси (l1 = l2 = 0,03). На трубопроводе имеются два плавных колена (zк = 0,15) и внезапное расширение (zвр).
 ,
, 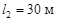 ) разного диаметра (d 1 = 0,1 м, d 2 = 0,15 м) при одинаковом коэффициенте Дарси (l1 = l2 = 0,03). Высоты слоя жидкости в баках: Н 1 = 4 м, Н 2 = 2 м.
) разного диаметра (d 1 = 0,1 м, d 2 = 0,15 м) при одинаковом коэффициенте Дарси (l1 = l2 = 0,03). Высоты слоя жидкости в баках: Н 1 = 4 м, Н 2 = 2 м. ; d = 0,1 м); коэффициент Дарси принять l = 0,022.
; d = 0,1 м); коэффициент Дарси принять l = 0,022.

 и одинаковым диаметром d = 0,15 м. Трубопровод смещен в середине пролета в горизонтальной плоскости с помощью двух плавных колен (zк = 0,44), установленных близко друг к другу.
и одинаковым диаметром d = 0,15 м. Трубопровод смещен в середине пролета в горизонтальной плоскости с помощью двух плавных колен (zк = 0,44), установленных близко друг к другу.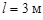 , Q = 1,5 л/с. Принять коэффициент Дарси l = 0,035, режим – турбулентный, zз = 9,3.
, Q = 1,5 л/с. Принять коэффициент Дарси l = 0,035, режим – турбулентный, zз = 9,3.

 ;
;  ; d 1 = 100 мм; d 2 = 200 мм; d н = 80 мм.
; d 1 = 100 мм; d 2 = 200 мм; d н = 80 мм. указанные на схеме местные сопротивления. Построить пьезометрическую линию для трубопровода в целом.
указанные на схеме местные сопротивления. Построить пьезометрическую линию для трубопровода в целом.


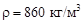 со средней скоростью v = 1,1 м/с.
со средней скоростью v = 1,1 м/с.
















 при перекачке 600 т/сут и работе насоса по перекачке 8 ч/сут.
при перекачке 600 т/сут и работе насоса по перекачке 8 ч/сут.


