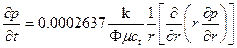Первоначальные, внутренние и внешние условия границ коллектора

Уравнение диффузии описывает как давление флюида в каком-нибудь кусочке горной породы будет реагировать на возбуждение давления. Для того, чтобы описывать физическую проблему это уравнение должно быть дополнено набором первоначальных состояний и состоянием границ коллектора.

Первоначальные условия: полное описание действия давления во всем пласте должно быть дано в такое-то время (данное время). В аналитической модели общее допущение должно быть такое: коллектор под постоянным давлением pi, время равно 0.

Условия внутренних границ:предусматривает условия потока жидкости скважин(ы) во время добычи или нагнетания. Эти состояния потока жидкости определяются законом Дарси адаптированным к геометрии скважины (стандартная, трещиноватая, наклонная, горизонтальная и т.д.). В основном, поток в поверхностных условиях постоянен во время 0, а в пластовых условиях подчиняется скоротечным изменениям (transient change) называемым эффект хранения у ствола скважины (wellbore storage). Кроме того, могут быть разрывы (перерывы) давления в пласте называемые скин-эффектом. Поэтому, условия внутренних границ будут комбинацией закона Дарси, wellbore storage и скин-эффекта.

Условия внешних границ:эти условия описывают внешние границы резервуара (коллектора). Какие бы ни были геометрические состояния, 3 основные условия границ коллектора используются в аналитической модели: уплотнение? (sealing), постоянное давление и во время бесконечной модели пласта (то есть, нет границ коллектора в данном направлении). (детали в §E.4).

• Простой пример: однородная линейно-поточная скважина, однородный безграничный коллектор. Простейший пример – однородная линейно-поточная скважина. Уравнения определяющие этот пример здесь (детали в §E.5):

 

Радиальное рассеивание в однородном коллекторе:

 

 

Первоначальное состояние:

 

 

Скважинное состояние:

 

Бесконечный коллектор:

 

 

• Безразмерные величины

Вышеприведенные уравнения включают в себя физические параметры, такие как проницаемость, и могли бы быть бесполезными в решении этой проблемы с особым сочетанием значений этих параметров. Безразмерные величины предназначены, чтобы устранять физические параметры, которые затрагивают количественно, но не качественно, действия коллектора.

Процесс выбора различных безразмерных величин прост (детали в §E.6). Для линейно-поточной скважины формулы безразмерных величин здесь:

 

Безразмерное расстояние:

 

Беспредельное давление:

 

Беспредельное время:

 

и в безразмерном выражении:

 

Радиальное рассеивание в однородном коллекторе:

 

 

Первоначальное состояние:

 

Скважинное состояние:

 

Бесконечный коллектор:

 

 

Эти уравнения независимы от физических параметров и могут быть решены необычным путем. Это изменение величин может быть использовано в запутанных случаях, но может повлечь за собой необходимость введения дополнительных величин, таких как (в этом случае) скин фактор, коэффициент безмерного сохранения у ствола скважины (dimensionless wellbore storage) и т.д.