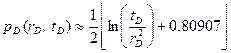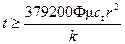Решение проблемы
Решение может быть сложным процессом, особенно потому, что решение не должно быть только действенным, но также должно быть выполнено на компьютере при сносной, недорогой цене последнего. Обычно проблему диффузии можно решить «как есть», или используя преобразования Лапласа или Фурье. Преобразование Лапласа очень популярно, так как оно упрощает уравнения разделяя время и место, и из-за процесса дополнения коэффициента сохранения в стволе скважины, скин-эффекта, двойной пористости и эффектов многослойного коллектора, и потому вполне прост в использовании. Конечно, мы не будем рассматривать детально процесс решения здесь. Даже в математическом приложении (смотр. §E.7) мы подробно излагали только проблему линейного потока. Экспоненциальный интеграл: в случае с линейным потоком флюида скважины в однородном (гомогенном) и безразмерном (неопределенны границы) коллекторе решение будет таким:
где Ei – экспоненциальный интеграл. По этому случаю решение линейного потока скважины иногда называется решением экспоненциального интеграла. Заменяя члены безразмерности ихними значениями мы получаем:
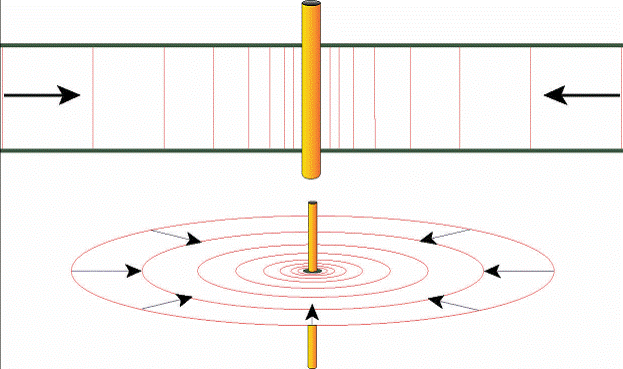
• Бесконечно действующий радиальный поток (infinite acting radial flow)
После того, как эффекты в стволе скважины становятся незначительными и до того, как выявляются границы слоев коллектора, поток может достичь состояния называемого Бесконечно действующий радиальный поток (БДРП – IARF). В случае с решением линейно действующего потока описанного выше, этот режим соответствует приблизительно функции экспоненциального интеграла. Если это указать в безразмерных выражении (см. §E.8):
For и в физическом выражении: For Если мы рассмотрим действие в стволе скважины (то есть когда r=rw и rD=1), позднее во времени приближение к решению радиального потока будет заключать в себе дополнительный элемент соответствующий падению или восстановлению давления в пласте (sandface), называемый скин фактор, S (описывается позже).
For
И в физическом выражении:
For
Эта связь, с давлением касательно логарифма времени в радиальном потоке, является принципиальной в интерпретации замеров скважин.
|