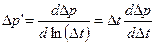B.7 • Билогарифмический (log-log) подход

· Безразмерные величины

Источники безразмерных величин и пути их получения описаны в §E.6. В действительности любая величина или переменная может быть безразмерной, если умножить ее на группу констант с противоположными величинами, но выбор этой группы будет зависеть от типа проблемы которую надо решить. Например, чтобы создать безразмерное давление, реальное давление p (в psi) умножают на группу «А» с единицами измерения psi-1.

 

Безразмерное давление: pD = A.p, где A = f (kh, m,..)

Безразмерное время: tD = B.t, где B = f (k, j, Ct..)

 

Определяя безразмерное давление и безразмерное время в этом случае возможно разработать аналитическую модель скважины и коллектора, или теоретическую «типовую модель кривой», которая дает нам всеобъемлющее «глобальное» описание поведения давления что независит от дебита или от действительных значений параметров скважины и коллектора (в группах А и В).

 

В билогарифмическом графике: log(pD) = log(p)+log(A) и log(tD) = log(t) +log(B)

 

Если выбрана правильная безразмерная модель, реальное (log p vs log t) и теоретические (log pD vs log tD) давления в зависимости от кривых времени похожи в очертаниях, но перемещаются параллельно (не могу найти подходящий перевод) друг-другу когда прочерчены в одном и том же графике. Изменения в значениях констант в группах А и В могут повлечь за собой перемещение данных на X и Y осях координат, но фигуры кривых будут оставаться без изменений.

Как только определена модель и установлено сопоставление, сдвиг между реальными данными и безразмерной типовой моделью кривой на обеих осях координат предоставляет нам решения на некоторые параметры интерпретации. Типично, что эффект сохранения в стволе скважины (wellbore storage) (C) определяется в подгонке времени (time match), или при смещении на X оси, а исходные данные слоя проницаемости (permeability-thickness) (kh) на оси Y. Окончательная подгонка типовой модели кривой дает нам скин (S).

Двойной логарифмический или билогарифмический подход теперь вытеснил полулогарифмический подход в индустрии, так как комбинируя билогарифмич. график p vs t с производной давления (pressure derivative), как описывается в следующем разделе, появляется возможность делать полный анализ с одним графиком. От простейшей модели однородного бесконечного коллектора до наиболее сложной модели неоднородного, имеющего границы коллектора, билогарифмический «диагностический» график обеспечивает нас качественной картиной скважины и коллектора, и количественным определением параметров.

 

Детали вычисления даны в §E.11.

Когда мы вносим реальные данные по давлению в тот же график, что и типовые модели безразмерных кривых, они немного смещены от этих кривых по Х-оси и Y-оси:

 

 

Перемещая имеющиеся данные к типовой модели кривых (или как Сапфир делает это наоборот) возможно определить некоторые параметры скважины и коллектора:

 

 

Это простой пример однородного коллектора, но этот же принцип применим и ко всем остальным.

 

B.8 • Производная давления (pressure derivative)

Представление производной давления в 1983 году преобразило науку по интерпретациям замеров скважин, которая в то время базировалась на полулогарифмическом графике. Помещением графика производной давления в билогарифмический график, родился «диагностический график», который был показан на предыдущих примерах.

Производная давления является, по существу, темпом изменения давления касательно функции суперпозиции времени – т.е. наклон кривой полулогарифмического графика:

 

Итак, основная идея производной – вычислить наклон на каждой точке кривой по давлению в полулогарифмическом графике (график суперпозиции), и отразить это в билогарифмическом графике.

Детали уравнения даны в §E.12. Подводя итог, производная для идеального падения давления (депрессии) (drawdown) имеет выражение:

 

 

· Чистый эффект сохранения в стволе скважины

В самом начале, когда поток регулируется компрессией/декомпрессией жидкости в стволе скважины (эффект сохранения), изменение давления линейное по отношению к проходящему времени:

 

 

Когда поток в начале соотносится с эффектом сохранения в стволе, кривые давления и производной от давления будут обьединяться в наклоне прямой линии в билогарифмическом графике.

 

· Бесконечно действующий радиальный поток

Как уже было показано, в радиальном потоке производная стабилизируется и дает постоянное значение, относительно наклона кривой суперпозиции m’.

В большинстве других режимов дебита будет видно, что тогда как билогарифмический график раскрывает небольшую или же ненужную информацию, кривая производной давления всегда показывает характерные данные.