B.10 • Польза метода суперпозиции в моделировании изменений по дебиту и моделировании границ
Логарифмическое приближение решению уравнения рассеивания (коэффициента диффузии) для бесконечно действующего радиального потока было представлено в §B.2. Эта аналитическая модель развита допуская единичный постоянный дебит, тогда как на практике нам нужно получить решение модели для более сложных предысторий потока скважины. В особенности, из-за трудности держать постоянным дебит скважины, методы интерпретации традиционно базировались на данных по восстановлению давления, предшествовавшим, конечно же, одному или двум падениям давления. Принцип суперпозиции позволяет вычислить действия многодебитного потока простым путем: добавлением данных по падению давления.
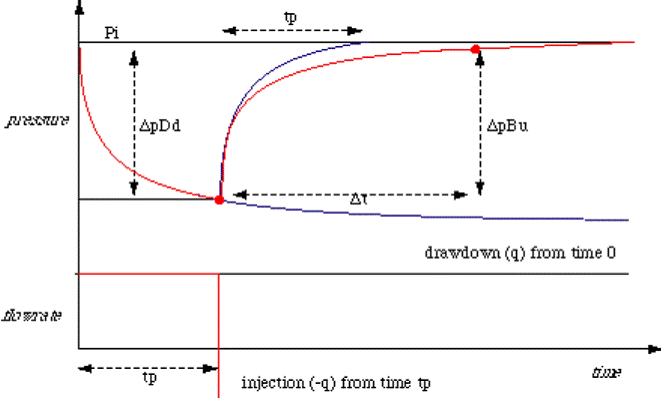
· Метод суперпозиции в восстановлении давления Рассматривая скважину с дебитом q работающую до конца времени tp, и затем закрывающуюся, мы хотим найти давление во время tp+t, как видно внизу. Тот факт, что уравнения линейны позволяет нам использовать принцип суперпозиции (наложения): изменение давления происходящее из-за соотношения периодов добычи равняется суперпозиции отдельных изменений давления вследствие каждой фазы добычи. Закрытие во время tp математически эквивалентно продолжению падения давления во время добычи с дебитом q; в сочетании с закачкой с дебитом –q от времени tp (ниже):
В этом случае, изменение давления во временном периоде tp+Dt будет суммой изменения давления вследствие падения давления во время добычи с дебитом q начиная со времени 0 до времени tp+Dt, а изменение давления во время нагнетания (закачки) с дебитом –q начиная со времени tp до времени tp+t:
pBU t pi pDD tp t pDD t
Снова ссылаясь на диаграмму, отмечаем, что после срока действия восстановления давления tp, изменение давления во время закачки с дебитом q такое же, как и изменение давления в конце падения давления: Если бы это не было для продолжавшегося действия падения давления, восстанавливающееся давление следовало бы зеленой линии и вернулась бы к значению Pi (pressure initial – начальное давление) после периода времени tp. Однако, это изменение наложено на «движующуюся основную линию», которая является продолжением снижения давления во время депрессии скважины (drawdown), и восстановление давления не сможет вернуться к значению Pi после временного периода tp.
Мы больше беспокоимся изменениями давления, чем само реальное давление:
Таким образом:
Так как решение падения давления является увеличивающейся функцией времени, последнее продолжительнее чем любое из положительных периодов. Таким образом:
Первое выражение подтверждает, что действие восстанавливающегося давления будет ровнее чем действие падающего давления, а второе поясняет, что давление никогда не сможет превзойти первоначальное.
· Метод суперпозиции в многоступенчатом испытании
Суперпозиция в многоступенчатом испытании является естественным расширением суперпозиции восстановления давления к любому виду истории добычи скважины. Порядок (очередность) дебитов q1, q2,.... qN или соотвествующие периоды времени T1, T2,... TN, с соответсвующими началами по времени t1=0, t2,.... tN, будет приближен к сумме падений давления, начиная с самого начала каждого периода потока до текущего времени, то есть до конца, и к сумме соответсвующих дебитов q1, q2-q1,... qN-qN-1.
Если решение по падению давления принимается за значение Q:
Если период которым мы интересуемся – период добычи или падение давления в многоступенчатом режиме добычи, изменение давления, которым мы интересуемся будет соотвествовать формуле вверху. Выбранная Q будет последним стабилизированным дебитом. Детали даны в §E.17.
В случае закрытия скважины после многоступенчатой добычи, делающий интерпретацию инженер, также как и для простого восстановления давления, будет рассматривать изменение давления с тех пор как закрыли скважину. Детали даны в §E.20.
|

 где
где 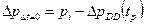

 и
и 





