РУБИНОВОГО ЛАЗЕРА
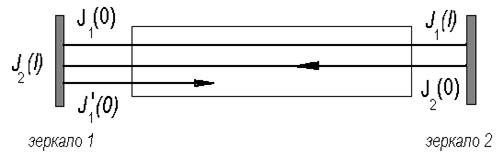
Поместим образец активного вещества длиной l между двумя зеркалами открытого резонатора, имеющими коэффициенты отражения соответственно r 1 и r 2 (рис. 5).
Рис. 5. Прохождение излучения через активное вещество в резонаторе
Изменение интенсивности излучения при прохождении через активное вещество длиной l может быть представлено следующим выражением:
где b - коэффициент внутренних потерь в активном веществе, который для кристалла рубина лежит в пределах 0,05…0,1 (1/см) = 5…10 (1/м). Рассмотрим последовательно прохождение излучения через активное вещество. Предположим, что на вещество со стороны первого зеркала падает излучение с интенсивностью J 1(0), тогда на втором зеркале получаем
От второго зеркала отражается излучение с интенсивностью J 2(0) = r 2× J 1(l). Снова пройдя в активной среде расстояние l, поток излучения падает на первое зеркало с интенсивностью
и отражается от первого зеркала
Для того, чтобы в объеме между зеркалами излучение не затухало, необходимо выполнение следующего условия:
Прологарифмировав последнее выражение, получаем
где bизл – коэффициент потерь на излучение; bэ – суммарный коэффициент потерь. Следовательно, условие генерации излучения можно записать через инверсию населенностей в виде
Введем определение пороговой инверсии населенностей
Преобразуем выражение (9) для порогового значения инверсии населенностей, тогда, введя обозначение
Коэффициент К пор является важной энергетической характеристикой излучения твердотельного лазера и определяет пороговый уровень мощности накачки
где hнак - КПД системы накачки. Величина К пор может быть определена из соотношения (20) с учетом (19) в соответствии со следующим выражением:
из которого, в свою очередь, можно выразить коэффициент внутренних потерь в активной среде b
Из приведенных выражений следует, что если в среде отсутствуют потери, т.е. bэ = 0, то К пор = 1. Теперь проведем приближенный расчет мощности излучения ОКГ на рубине. Запишем уравнение (16) отдельно для прямой и отраженной волн (рис. 5)
Решим эту систему уравнений с учетом выражения для инверсии населенностей (9), полученного из балансных уравнений, при выполнении граничных условий
Предположим, для начала, что в кристалле рубина отсутствуют внутренние потери, т.е. b = 0. Решив систему (24) для указанных граничных условий и опустив при этом промежуточные вычисления, получим выражение, определяющее интенсивность излучения рубинового лазера без учета внутренних потерь
где J изл – интенсивность излучения ОКГ на рубине; К – коэффициент, определяющий превышение мощности накачки над пороговым уровнем мощности накачки. Коэффициент К может быть выражен как отношение мощности накачки, поглощаемой кристаллом рубина, к пороговой мощности накачки при условии отсутствия потерь, т.е.
Мощность накачки, поглощаемая кристаллом рубина, зависит от величины напряжения, приложенного к пластинам конденсатора блока питания системы накачки, и определяется выражением
где С = 1400 мкФ – емкость конденсаторов блока питания системы накачки; U нак. – напряжение накачки; tнак. = 10-3 с – длительность импульса накачки. Пороговая мощность накачки (знаменатель в (26)) была рассчитана теоретически в соответствии с (14) п. 4 в предположении, что в активной среде отсутствуют потери (b = 0) и КПД системы накачки hнак = 1. Следовательно, коэффициент К может быть определен посредством следующего выражения:
Мощность индуцированного излучения ОКГ на рубине, без учета внутренних потерь, можно определить исходя из следующего соотношения:
где f 21 = 4,321×1014 – частота перехода с рабочего уровня на основной уровень; S т – площадь торца кристалла рубина, которая для размеров, выбранных в п. 4: l = 0,1 м и R = 3×10-3 м, составляет S т = 2,827×10-5 м2. Подставляя в указанное соотношение выражение, определяющее интенсивность излучения рубинового лазера (без учета потерь) (25), получаем
Потери b в кристалле рубина можно учесть, если ввести эквивалентную длину рубинового стержня l э, воспользовавшись следующим соотношением:
откуда с учетом (18) можно выразить l э
Подставив в (29) вместо l выражение для l э получим выражение, определяющее мощность индуцированного излучения рубинового лазера с учетом потерь в кристалле рубина
При мощности накачки значительно больше пороговой, т.е. при К >> 1, можно воспользоваться приближенным выражением для нахождения мощности излучения рубинового лазера:
Из приведенных формул (30) и (31) очевидно, что мощность индуцированного излучения рубинового лазера зависит от целого ряда параметров, связанных как с характеристиками системы накачки, так и с конструктивными особенностями лазера.
|

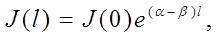 (16)
(16) - коэффициент квантового усиления;
- коэффициент квантового усиления;


 или
или  (17)
(17) или
или  (18)
(18)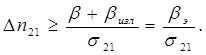
 (19)
(19) и пренебрегая вероятностью собственного излучения лазера 2Р21, получаем
и пренебрегая вероятностью собственного излучения лазера 2Р21, получаем (20)
(20) (21)
(21) (22)
(22) (23)
(23) (24)
(24)
 (25)
(25) (26)
(26) (27)
(27) (28)
(28)
 (29)
(29)

 (30)
(30) (31)
(31)


