ДЛЯ ОКГ НА РУБИНЕ
Кинетические уравнения для трехуровневой системы, представленной на рис. 4, имеют вид:
Для установившегося распределения частиц в рассматриваемой системе, когда
исходя из (4) и (5), запишем уравнения баланса энергий в квантовой системе
Выразим из уравнений баланса (7) соотношение, определяющее инверсию населенностей на рабочих уровнях
Рассмотрим теперь два предельных случая: 1. Пусть вероятность релаксационных переходов Г32 между уровнем накачки и рабочим уровнем рассматриваемой квантовой системы намного превышает вероятности других возможных переходов, т.е. Г32 >> А31, Р31, А21, Р21. Тогда из соотношения (8) получаем
Это же соотношение можно получить из второго и третьего уравнений баланса в системе (7), если учесть, что Г32 >> А31, Р31. 2. Пусть вероятность индуцированных переходов с уровня накачки на основной уровень превышает вероятности других возможных переходов, т.е. Р31 >> А31, Г32, А21, Р21. Тогда, исходя из (8) получаем
Из полученных выражений (9) и (10) следует, что для выполнения условия инверсии населенностей необходимо, чтобы вероятность индуцированных переходов между уровнем накачки и основным уровнем превышала вероятность спонтанных переходов между рабочим и основным уровнями, т.е.
|

 (3)
(3)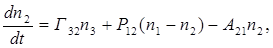 (4)
(4) (5)
(5) (6)
(6)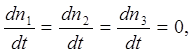
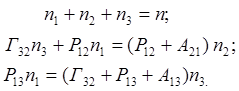 (7)
(7) , таким образом, чтобы в правой части этого выражения находились только известные величины (вероятности переходов и полное число частиц в квантовой системе n). Опустив промежуточные выкладки, получаем
, таким образом, чтобы в правой части этого выражения находились только известные величины (вероятности переходов и полное число частиц в квантовой системе n). Опустив промежуточные выкладки, получаем (8)
(8) (9)
(9)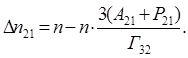 (10)
(10) (11)
(11)


