Дифференциальное уравнение теплопроводности
Математическое описание температурных полей в компонентах технологических систем выполняется с помощью дифференциального уравнения теплопроводности. Выведем это уравнение при следующих допущениях [3]: твердое тело однородно и изотропно; в процессе теплопередачи не происходят фазовые превращения; деформация, вызванная изменением температуры пренебрежимо мала по сравнению с размерами тела. Выделим из нагреваемого тела элементарный объем (рис. 1.4) DV, где DV = Dx × Dy × Dz. На основании закона изменения внутренней энергии dU= dQ1+ dQ2 , (1.13) где dU – общее изменение внутренней энергии вещества в объеме DV за время Dt; dQ1 – количество теплоты, поступившее в этот объем путем теплопроводности; dQ2 – количество теплоты, возникшее в объеме ΔV в связи с функционированием в нем внутренних источников. К внутренним относятся
dQx = qx × Dy × Dz × dt теплоты, где qx – плотность теплового потока в направлении оси ОХ. Через противоположную площадку А2В2С2Д2 за это же время отводится dQx+Dx теплоты, причем dQx+Dx = qx+Dx × Dy × Dz × dt. Разность: dQ1x = dQx - dQx + Dx = (qx - qx + Dx) × Dy × Dz × dt, (1.14) представляет собой количество теплоты, поступившей в объем DV за счет теплопередачи в направлении оси ОХ. Функция qx+Dx непрерывна в интервале Dx, поэтому она может быть разложена в ряд Тейлора:
Ограничимся первыми двумя членами ряда, поскольку остальные содержат малые величины высоких порядков. Тогда уравнение (1.14) преобразуется:
Аналогичные выражения можно получить для определения количества теплоты, поступившей в объем DV по направлениям OY и OZ. Суммируя величины dQ1x, dQ1y, dQ1z, получаем:
Определим величину dQ2. Если объемную плотность тепловыделения внутренних источников обозначить qв., то за время dt в объеме DV накопится теплота: dQ2 = qв. × DV × dt. (1.18) Элементарные количества теплоты dQ1 и dQ2 вызовут изменение температуры вещества и величину dU можно найти из уравнения:
где с – массовая теплоемкость, Дж/(кг×К), ρ; – плотность вещества, кг/м3. Подставляя значения dQ1, dQ2, dU из уравнений (1.17) – (1.19) в уравнение (1.13), получим:
Но по закону Фурье: Тогда:
Так как коэффициент теплопроводности зависит от температуры, то дифференциальное уравнение теплопроводности в общем виде имеет выражение (1.21). Более простой вид уравнения получается после принятия упрощающих допущений. Наиболее часто применяют следующие допущения: 1) коэффициент теплопроводности не зависит от температуры; 2) плотность внутренних источников тепла равна 0, (qв = 0):
где Таким образом, в наиболее простом виде дифференциальное уравнение теплопроводности выглядит так:
где Ñ2 – оператор Лапласа. Выражения (1.23) и (1.22) представляют собой нелинейные дифференциальные уравнения в частных производных второго порядка. Аналитическое решение нелинейных дифференциальных уравнений достаточно сложно и они могут быть решены только в простейших случаях теплообмена. Намного легче решаются линейные дифференциальные уравнения т. к. они обладают важной особенностью известной из математики: сумма нескольких независимых друг от друга решений линейного дифференциального уравнения также является решением такого уравнения. Это свойство позволяет в случаях, когда на тело действует система из нескольких независимых источников описать их воздействие независимыми дифференциальными уравнениями, решить их, а затем общее решение представить в виде суммы частных (принцип суперпозиции решений).
|

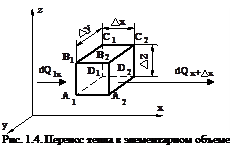 источники, тепловыделение которых связано с процессами, происходящими в материале твердого тела, например, с объемными химическими реакциями, действием электрического тока и т. д. Пусть за время dt к элементарной площадке А1В1С1Д1 подведено
источники, тепловыделение которых связано с процессами, происходящими в материале твердого тела, например, с объемными химическими реакциями, действием электрического тока и т. д. Пусть за время dt к элементарной площадке А1В1С1Д1 подведено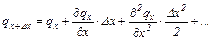 (1.15)
(1.15)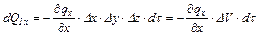 . (1.16)
. (1.16)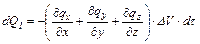 . (1.17)
. (1.17)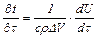 , (1.19)
, (1.19)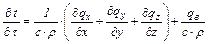 . (1.20)
. (1.20)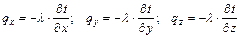 .
.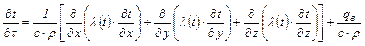 . (1.21)
. (1.21)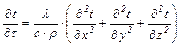 , (1.22)
, (1.22)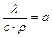 – коэффициент температуропроводности данного вещества. Он характеризует тепловую инерцию материала. Чем выше а, тем быстрее материал прогревается.
– коэффициент температуропроводности данного вещества. Он характеризует тепловую инерцию материала. Чем выше а, тем быстрее материал прогревается. , (1.23)
, (1.23)


