Закон распределения интенсивности источника
Закон распределения интенсивности (плотности теплового потока) является одной из важнейших характеристик источника. В процессах механической обработки, как правило, возникает несколько источников теплоты. Чтобы для каждого из них установить тепловую мощность, необходимо: 1) определить общую тепловую мощность процесса; 2) распределить последнюю между конкретными источниками, возникающими в данной технологической операции, то есть составить приходную часть теплового баланса (см. уравнение (1.1)). Если тепловая мощность данного источника (Q, Дж/с) распределенного по некоторому объему, расположенному в системе координат X, У, Z, то между элементом тепловой мощности dQ и интенсивностью источника q (x, y, z) существует очевидное соотношение: dQ (x, y, z) = q (x, y, z)dx dy dz. (2.1) В реальных технологических процессах распределение интенсивности источников описывается сложными закономерностями. При теплофизическом анализе прибегают к некоторым идеализированным законам распределения интенсивности источников и стоков в пространстве и во времени [3]. Рассмотрим некоторые идеализированные законы, часто встречающиеся при теплофизическом анализе процессов механической обработки материалов. Самым простым является равномерное стационарное распределение, когда интенсивность q0 не зависит от координат и времени.
Соответственно для трех-, двух- и одномерного источников, что отмечено индексами при q. Следующую группу представляют источники с линейно распределенной интенсивностью. В качестве примера рассмотрим линейный призматический источник, ограниченный в трех направлениях, интенсивность которого в двух направлениях распределена по линейным законам, а в третьем – равномерно (рис. 2.2). Для этого источника q (x, y, z) = qo – k1 x – k2 y. (2.2) Из условий q (ℓ, 0, z) = 0 и q (x, ∆, z) = 0 получаем:
Тогда:
Откуда:
Следовательно:
где по оси ОХ и равномерного по оси OZ. Используя (2.1), получаем при u = exp [-3] = exp [-k×ℓ] @ 0,047. Поэтому если источник в точке х = ℓ;имеет интенсивность, близкую к нулю, можно положить k×ℓ» 3, и k=3/ℓ;
Большую группу идеализированных источников составляют источники с распределением интенсивности по нормальному закону. К этой группе относятся нормально-линейные, нормально-плоские (полосовые), нормально-круговые и нормально объемные источники теплоты. Общим для этих источников является то, что распределение интенсивности вдоль одной, двух или трех осей координат подчиняется закону нормального распределения. На рис. 2.3 приведен двумерный ограниченный источник длинной b и шириной 2ℓ;. Вдоль оси ОХ он имеет закон распределения: q (x) = q0 exp [-k × x2], (2.6)
известно, что:
где Ф(рu) – функция интеграла вероятности Гаусса, иногда обозначаемая erf [pu]. Используя формулу (2.7), получаем:
В правой части выражения учтено, что при Нормально-круговой двумерный источник описывается уравнением
где Большое распространение имеют комбинированные источники. Рассмотрим источник, в котором на первой части контактной площадки теплота распределена равномерно, а на второй – по некоторой убывающей кривой, которая хорошо аппроксимируется экспонентой.
Рис. 2.3. Нормально распределенные источники: полосовой и круговой Для него:
Рис. 2.4. Источник с комбинированным законом распределения Определив q0 , получаем формулы для описания законов распределения интенсивностей: при при где
|





 .
.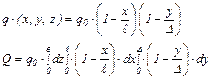
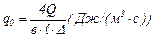 . (2.3)
. (2.3) . (2.4)
. (2.4) – безразмерные абсцисса и ордината любой точки внутри источника. На рис. 2.2 приведен двумерный источник с распределением интенсивности по экспоненциальному закону q(x) = q0 exp [-kx]
– безразмерные абсцисса и ордината любой точки внутри источника. На рис. 2.2 приведен двумерный источник с распределением интенсивности по экспоненциальному закону q(x) = q0 exp [-kx] . (2.5)
. (2.5)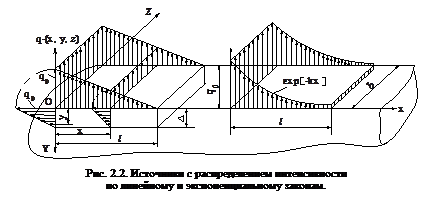
 . (2.7)
. (2.7)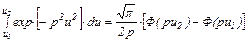 , (2.8)
, (2.8) . (2.9)
. (2.9)
 (2.10)
(2.10) – безразмерный текущий радиус.
– безразмерный текущий радиус.
 (2.11)
(2.11)
 ,
, , (2.12)
, (2.12)
 .
.


