Плотность итоговых потоков теплообмена
Плотность итоговых потоков теплообмена определяют путем решения балансовой задачи при граничных условиях 4-го рода (см. п. 3.3.4). В этом случае приравнивают друг другу средние температуры соприкасающихся тел на каждой контактной площадке. Для площадки ab:
где в левой части уравнения – температура площадки контакта, рассчитанная исходя из закономерностей распределения теплоты в теле А, в правой – то же в теле В. Аналогично для площадок cd и ef:
Как видно из примера, необходимо составить столько уравнений, сколько контактных площадок имеется в системе. В эти уравнения входят средние температуры, значения которых зависят от известных плотностей потоков теплообразующих источников W и от неизвестных плотностей итоговых потоков теплообмена Q. Поскольку число неизвестных равно числу уравнений, полученная система имеет единственное решение. В результате решения такой системы каждый из итоговых потоков теплообмена может оказаться со знаком «+» или «-». Знак «+» показывает, что итоговый поток идет в том направлении, которое предусматривалось в структурной схеме.
Инженерная методика расчета температур На контактных площадках твердых тел
Методика расчета температур. Общие положения
Идея инженерной методики [4] состоит в том, что формулы для расчета температур представляют в виде ряда сомножителей, каждый из которых зависит от той или иной особенности источника теплоты и формы тела, на котором расположен источник. Учитывая тот факт, что методика позволяет определять избыточную над температурой окружающей среды температуру в ТС, для обозначения температуры будем использовать символ «θ;» вместо «t». Формула для расчета температур имеет вид: θ = АМ × АС × АР × АД × АК × АО ∙ АТ, (7.1) где АМ – коэффициент, зависящий от мерности источника теплоты; АС – коэффициент, зависящий от скорости перемещения источника теплоты; АР – коэффициент, зависящий от закона распределения источника теплоты; АД – коэффициент, зависящий от длительности функционирования источника теплоты; АК – коэффициент, зависящий от конфигурации зоны тепловыделения; АО – коэффициент, зависящий от ограниченности источника теплоты; АТ – коэффициент, зависящий от формы тела, на котором расположен источник теплоты. Формула (7.1) базируется на кодировании тепловых источников (уравнение (3.9)) и пригодна для расчета как средних θср ., так и наибольших θmax температур на контактной площадке. Поэтому каждый из сомножителей А может иметь обозначение Аср. в том случае, если рассчитывают среднюю температуру, и Аmax, если определяют максимальное значение температуры контакта. Опишем алгоритм расчета температур на контактных площадках тел. В общем случае этот алгоритм содержит три ветви, относящиеся к источникам различной мерности (М = 1; 2; 3). На рис. 7.1 показана ветвь для двумерных источников (М = 2), поскольку они наиболее часто встречаются при теплофизическом анализе технологических систем. Первый сомножитель в формуле (7.1)
где q0 – наибольшая плотность теплового потока, Вт/м2; ℓ; – определяющий (характерный) размер источника, м; l – коэффициент теплопроводности тела, Вт/(м×К). При расчете АМ для движущегося источника характерным считают размер площадки контакта по направлению движения источника. Для неподвижного источника в качестве характерного может быть выбран любой конечный размер источника. Но если рассматривают контакт между подвижным и неподвижным телами, то и для неподвижного источника в качестве характерного следует принимать размер в направлении перемещения движущегося тела. Второй множитель АС характеризует скорость перемещения источника.
Рис. 7.1. Алгоритм расчета температур на контактных площадках твердых тел
Для быстродвижущихся источников (С = 2, уравнение (3.9)):
где Pe – критерий Пекле (Pe ³ 10). Для неподвижных источников (С = 0):
Следующий коэффициент АР учитывает закон распределения плотности тепловых потоков. В зависимости от значения символов Р и С в коде источника (3.9) выбирают коэффициенты АР по табл. 7. Таблица 7 Коэффициенты АР
Коэффициент АД, учитывающий длительность функционирования источника, для установившегося теплообмена (Д = 2), а также для быстродвижущихся источников имеет значение АД = 1. При нестационарном теплообмене (Д = 1) значения АД (табл. 8) зависят от безразмерного времени, т.е. критерия Фурье (см. формулу (2.14)).
Таблица 8 Коэффициенты АД
Коэффициент АК учитывает конфигурацию площадки, на которой расположен источник. Если площадка имеет вид бесконечной полосы или прямоугольника (К = 1), то АК = 1. Для источника, имеющего форму круга (К = 2), коэффициенты АК в зависимости от законов распределения имеют значения, приведенные в табл. 9. Эти коэффициенты рассчитаны для условий стационарного теплообмена (Д = 2). Таблица 9 Коэффициенты АK для круговых источников при стационарном теплообмене
Коэффициент АО учитывает ограниченность источника. Если источник имеет вид неограниченной полосы (О = 1),то АО = 1. Такое же значение имеет коэффициент АО для кругового источника, поскольку его ограниченность учтена при расчете значений АК для прямоугольных источников, ограниченных в двух направлениях (О = 2, размер площадки b × ℓ;), значения АО зависят от безразмерного комплекса:
Влияние ширины быстродвижущихся источников на температурное поле различно при разных скоростях движения. Поэтому коэффициенты АО здесь зависят от значений безразмерного комплекса:
При u > 10 значения АОmax близки к единице, а АОср ., начиная от значения 0,87, медленно возрастают с увеличением u. Коэффициент АТ учитывает влияние формы нагреваемого тела. Для неограниченного тела (Т = 0) коэффициент АТ = 1. Для полубесконечного тела (Т = 1) с адиабатической границей коэффициент АТ = 2. В других случаях (Т > 1) коэффициенты АТ выбирают по табл. 10. В этой таблице приведены данные для пластин и цилиндров с адиабатическими граничными поверхностями (Т = 2 и Т = 7) при перемещении по ним быстродвижущегося источника (С = 2). Значения АТ рассчитывают по формулам, приведенным в таблице, в зависимости от:
где D – толщина пластины, м; ℓ; – характерный размер источника (рис. 7.3), м. Для цилиндра в формулу (7.7) вместо Δ; подставляют диаметр поверхности D, по которой движется источник (рис. 7.3, б). В табл. 10. даны значения коэффициентов АТ для случая, когда неподвижный (С = 0) источник расположен на одной из поверхностей полубесконечного клина с
адиабатическими поверхностями (рис. 7.3, в). Таблица 10 Коэффициент АТ
|

 , (6.14)
, (6.14) , (6.15)
, (6.15) . (6.16)
. (6.16) , (7.2)
, (7.2)
 , (7.3)
, (7.3) . (7.4)
. (7.4) . (7.5)
. (7.5)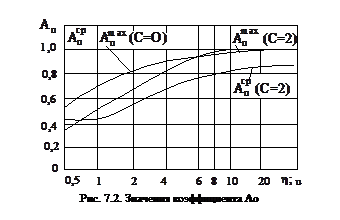
 . (7.6)
. (7.6) , (7.7)
, (7.7)




