Дерева и выход из него сортиментов.
Для выполнения данного задания необходимо изучить соответствующие разделы учебника, где освещаются вопросы формы древесного ствола и способы определения его объема. Исходными данными служат результаты обмера стволов срубленных деревьев, приведенные в настоящем методическом пособии (прил. 1). Вариант исходных данных устанавливается каждому студенту преподавателем. Объем ствола в коре и без коры вычисляют сначала по трем простым формулам: срединного сечения, двух концевых сечений и трех сечений (срединного и двух концевых), а затем по трем сложным стереометрическим формулам. Запись исходных данных и результаты вычислений ведется в бланке специальной формы, выдаваемом кафедрой. На этом бланке вычерчивается схема ствола с указанием соответствующих сечений и длин. Полученные результаты объема ствола в коре и без коры по всем формулам заносят на первую страницу бланка задания для последующего их анализа. Анализ заключается в получении абсолютных и относительных расхождений результатов приближенного определения объема ствола по простым и сложным формулам с истинным объемом. За истинный объем можно принять объем, вычисленный по сложной формуле трех сечений. Однако студенты должны представлять, что истинный объем можно получить только ксилометрическим способом. Сложные методы значительно точнее, но и они дают некоторые погрешности. Величина этих погрешностей чаще всего не превышает ±2 %. На основе полученных абсолютных и относительных погрешностей студент делает вывод о степени точности простых формул, какая из формул завышает, и какая занижает объем ствола и чем это объясняется, а также чем объясняется более высокая точность сложных формул по сравнению с точной формулой. Анализ результатов дается отдельно для объема в коре и без коры и излагается письменно на титульной стороне бланка. Кроме того, студенты определяют объемы сортиментов, которые можно заготовить из этого ствола. Разделка ведется от комля к вершине. В первую очередь выделяются наиболее крупные сортименты. При этом руководствуются требованиями ГОСТ 9463-88. «Лесоматериалы круглые хвойных пород» (прил. 7). Объемы сортиментов находят двумя способами: 1) по простой формуле срединного сечения; 2) по сложной формуле срединного сечения как сумму объемов нескольких двухметровых отрезков и их частей, составляющих длину сортимента. Объемы сортиментов в коре и без коры, найденные по простой формуле, сравнивают с объемами, найденными по сложной формуле, вычисляют процент расхождения между ними. На основе полученных расхождений делают вывод о причинах, влияющих на величину этих расхождений. Объем вершинки ствола определяется по формуле конуса:
где VВ – объем вершинки, м3; gL – площадь поперечного сечения основания вершинки, м2; h – длина вершинки, м.
Все объемы ствола и сортиментов находятся в кубических метрах с точностью до 0,0001 м3. На последней странице бланка зарисовывается схема разделки ствола на сортименты с указанием наименования сортиментов и их длин. Необходимые площади поперечных сечений ствола и сортиментов определяют по соответствующим диаметрам и формулам круга, или по таблицам площадей кругов. Такие таблицы содержатся в различных лесотаксационных справочниках. Все записи в бланках рекомендуется делать карандашом. Пример выполнения задания 1 приводится ниже.
Таблица 1 Пример выполнения задания 1 Исходные данные для заданий по таксации ствола дерева и его частей
V – объем ствола, м3; γ; – площадь поперечного сечения на половине ствола, м2; L – длина ствола без вершинки, м; Vв – объем вершинки, м3. 1. Порода дерева ─ Сосна 2. Диаметр на высоте груди, D в коре / без коры……………………… 27,2 / 25,2 см 3. Высота ствола, H …………………………………………………… 24,4 м 4. Диаметр на высоте 1/4 Н в коре / без коры …………. …………… 22,8 / 22,1 см 5. Диаметр на высоте 1/2 Н в коре / без коры ……………………… 18,8/18,4 см 6. Диаметр на высоте ¾ Н в коре / без коры ……………………… 11,9/11,6 см 7. Прирост по Д на высоте груди за 10 лет без коры ……………………… 1,9 см 8. Прирост по Д на 1/2 Н за 10 лет без коры ………………………………… 2,0 см 9. Прирост по высоте за 10 лет ………………………………………… 1,4 м 10. Рост: ─ слабый, умеренный, хороший 11. Возраст ……………………………………………………………… 75 лет 12. Число годичных слоев в последнем см по радиусу на высоте груди …. 8 13. Протяженность кроны ………………………………………………… 6,5 м Определение объема ствола по простым формулам: 1) по срединному сечению и длине (Губера):
а) в коре б) без коры 2) по двум концевым сечениям и длине (Смалиана): а) в коре б) без коры 3) по трем сечениям и длине (Ньютона─Рикке):
а) в коре Определение объема ствола по сложным формулам: 1) срединных сечений (Губера):
а) в коре
V ств = (γ;1 + γ;2 + γ;3 +…+ γ;n) l + V вер= (0,0598 + 0,0491 + 0,0419 + 0,0401 + 0,0366 + + 0,0305 + 0,0263 + 0,0214 + 0,0145 + 0,0093 + 0,0037)2 + 0,0014 = 0,6678 м 3 ; без коры 2) концевых сечений (Смалиана):
а) в коре V ств = + 0,0408 + 0,0384 + 0,0333 + 0,0283 + 0,0238 + 0,0177 + 0,0117 + 0,0062)]2 + 0,0014 = = 0,0360 + 0,6002 + 0,0014 = 0,6376 м 3 ;
б) без коры V ств = [ + 0,0227 + 0,0170 + 0,0111 + 0,0058)]2 + 0,0011 = 0,5933 м3.
3) сечений срединных и концевых (Рикке─Симпсона)
а) в коре V ств = [ g0 + gn+ 2 (g1+g2+ g3…+ gn-1) + 4 (γ1+ γ2+ γ3+ …+ γn) ]
+ 0,0238 + 0,0177 + 0,0117 + 0,0062) + 4 (0,0598 + 0,0491 + 0,0419 + 0,0401 + 0,0366 +
+ 0,0305 + 0,0263 + 0,0214 + 0,0145 + 0,0093 + 0,0037)] б) без коры V ств = [ 0,0547 + 0,0014 + 2 (0,0483 + 0,0423 + 0,0387 + 0,0366 + 0,0324 + 0,0272 +
+ 0,0227 + 0,0170 + 0,0111 + 0,0058) + 4 (0,0515 + 0,0449 + 0,0394 + 0,0377 + 0,0356 + + 0,0292 + 0,0252 + 0,0201 + 0,0137 + 0,0087 + 0,0034)] где V ств − объем ствола, м3 ; g0, g1, g2…. gn − площади поперечных сечений на концах отрезков, м2; γ1, γ2, γ3…. γ n − площади поперечных сечений на середине отрезков, м2; L − длина ствола без вершинки, м; l − длина отрезка, м; V вер− объем вершинки ствола, м3.
Результаты вычислений объема ствола по различным формулам записывают в табл. 2.
Таблица 2
После определения объема ствола по разным формулам ствол раскраивают на сортименты. Используя ГОСТ 9463−88 «Лесоматериалы круглые хвойных пород» (прил. 7) студенты выбирают наиболее ценные сортименты и заполняют таблицу. Для выбранных сортиментов указывают их класс крупности, длину, диаметр в верхнем отрезе в коре и без коры. Далее определяют объемы сортиментов по двух метровым отрезкам и по срединным сечениям в коре и без коры. Полученные объемы сортиментов по срединным сечениям сравнивают с объемами найденными по двух метровым отрезкам и определяют процент ошибки. Таблица заканчивается определением процента объема сортимента от объема ствола вычисленным по двух метровым отрезкам. В заключении данной работы студенты вычерчивают схему разделки ствола на сортименты и пишут вывод о точности вычислений объема ствола разными способами по сравнению со сложной формулой (Симпсона). Пример выполнения этого задания приводится в табл. 3.
Таблица 3
а) для расчетов по простым формулам б) для расчетов по сложным формулам
γ; γ1 γ2 γ3 γ4 γ5 γ6 γ7 γ8 γ9 γ10 γ11
Рис 1. Схемы ствола
|


 ;
;  .
. м 3;
м 3; м 3 .
м 3 .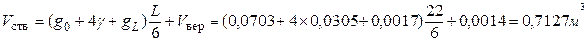 ; б) без коры
; б) без коры  .
.
 [
[  + (0,0543 +0,0456 +
+ (0,0543 +0,0456 + + (0,0483 + 0,0423 + 0,0387 + 0,0366 + 0,0324 + 0,0272 +
+ (0,0483 + 0,0423 + 0,0387 + 0,0366 + 0,0324 + 0,0272 + + V вер = =[0,0703 + 0,0017 + 2 (0,0543 + 0,0456 + 0,0408 + 0,0384 + 0,0333 + 0,0283 +
+ V вер = =[0,0703 + 0,0017 + 2 (0,0543 + 0,0456 + 0,0408 + 0,0384 + 0,0333 + 0,0283 + + 0,0014 = 0,6697 м3 ;
+ 0,0014 = 0,6697 м3 ;
 30,7
30,7
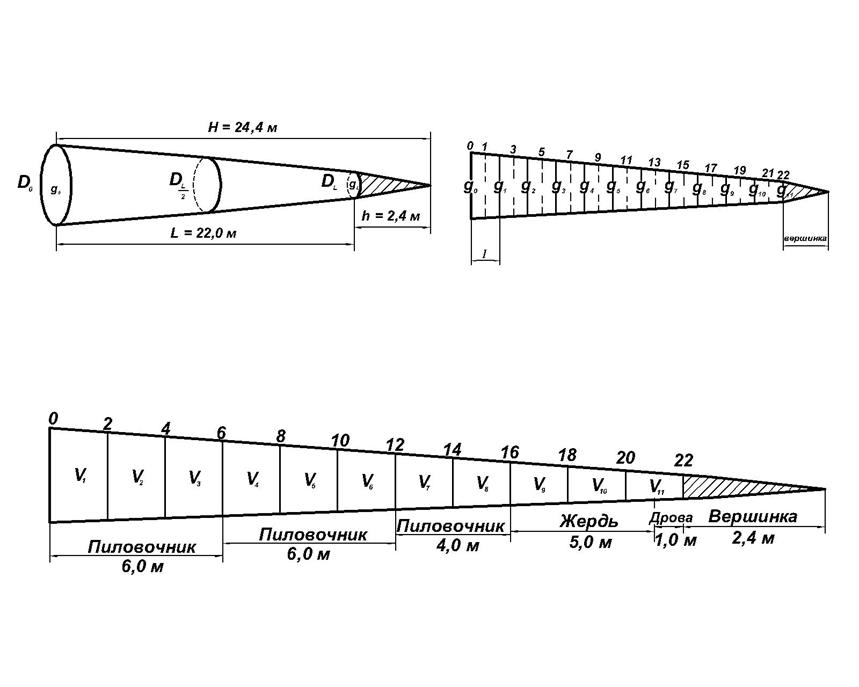

 в) для разделки ствола на сортименты
в) для разделки ствола на сортименты


