В качестве следующей характеристики формы ствола используется группа параметров, расчет которых полностью основан на данных о сбеге. Общепринято использование четырех относительных диаметров, которые получили название коэффициентов формы:



 ,
,
где 

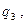
 - коэффициенты формы,
- коэффициенты формы,  - диаметры соответственно на нулевой высоте ствола, на высоте груди, на четвертой части высоты ствола, на половине высоты и на трех четвертях высоты.
- диаметры соответственно на нулевой высоте ствола, на высоте груди, на четвертой части высоты ствола, на половине высоты и на трех четвертях высоты.
 Каждый коэффициент в отдельности характеризует сбег той части ствола, к которой он относится. Взятые вместе они достаточно точно позволяют судить о форме всего ствола, степени его сбежистости, объеме, характере и размере лесоматериалов, которые можно получить из ствола.
Каждый коэффициент в отдельности характеризует сбег той части ствола, к которой он относится. Взятые вместе они достаточно точно позволяют судить о форме всего ствола, степени его сбежистости, объеме, характере и размере лесоматериалов, которые можно получить из ствола.
Наиболее изучен коэффициент  он, в частности, используется при расчете другого показателя формы ствола, который получил название видового числа. Первые исследователи в поисках обобщающего показателя формы ствола пришли к единому мнению, что сравнение объема ствола с объемом цилиндра, имеющего с ним одинаковую высоту и площадь основания, равную площади сечения на высоте груди, хорошо описывает степень приближения объема ствола к объему такого цилиндра. Установленное таким способом видовое число получило название старого видового числа:
он, в частности, используется при расчете другого показателя формы ствола, который получил название видового числа. Первые исследователи в поисках обобщающего показателя формы ствола пришли к единому мнению, что сравнение объема ствола с объемом цилиндра, имеющего с ним одинаковую высоту и площадь основания, равную площади сечения на высоте груди, хорошо описывает степень приближения объема ствола к объему такого цилиндра. Установленное таким способом видовое число получило название старого видового числа:
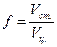 ,
,
где 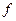 – видовое число (старое в данном случае),
– видовое число (старое в данном случае),  – объемы ствола и цилиндра. Старое видовое число дает качественную характеристику формы ствола, получившую название полнодревесность:чем больше видовое число, тем в большей степени объем ствола приближается к объему цилиндра, то есть тем более ствол полнодревесен, и наоборот. Точность расчета видового числа по приведенной формуле зависит от точности определения объема ствола. Более поздние исследования обосновали расчеты видовых чисел на иных зависимостях:
– объемы ствола и цилиндра. Старое видовое число дает качественную характеристику формы ствола, получившую название полнодревесность:чем больше видовое число, тем в большей степени объем ствола приближается к объему цилиндра, то есть тем более ствол полнодревесен, и наоборот. Точность расчета видового числа по приведенной формуле зависит от точности определения объема ствола. Более поздние исследования обосновали расчеты видовых чисел на иных зависимостях:  – этот способ основан на определении объема по простой формуле через срединное сечение ствола, поэтому дает невысокую точность; хорошую точность (
– этот способ основан на определении объема по простой формуле через срединное сечение ствола, поэтому дает невысокую точность; хорошую точность ( 3 %) определения видового числа дает формула Шиффеля:
3 %) определения видового числа дает формула Шиффеля:
 .
.
Эта формула устанавливает зависимость видового числа от коэффициента формы и высоты; известен также ряд эмпирических формул, в частности, для сосны:  – 0,20, для ели
– 0,20, для ели  .
.
Еще один способ определения видового числа, основанный на массовом статистическом материале, разработал проф. М.Е. Ткаченко. Составленные им таблицы Всеобщих видовых чисел (прил. 10), в которых представлена зависимость 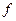 от
от  и
и  , позволили сформулировать закон, согласно которому стволы всех древесных пород, растущих в насаждениях, в любых условиях, при равной высоте, диаметре и коэффициенте формы, имеют почти равные видовые числа, а следовательно, и объемы.
, позволили сформулировать закон, согласно которому стволы всех древесных пород, растущих в насаждениях, в любых условиях, при равной высоте, диаметре и коэффициенте формы, имеют почти равные видовые числа, а следовательно, и объемы.
Используя данные своего варианта и приведенные выше формулы, студенты выполняют расчеты согласно примерам приведенных в табл. 5 и 6.
| Определение коэффициентов формы и видовых чисел ствола
|
| Коэффициенты в коре
формы без коры
| Видовые числа в коре, вычисленные по:
|
| q0
| q1
| q2
| q3
| отношению
Vcтв
Vцил
(точное)
| формуле
f=q22
| таблице проф. М.К. Ткаченко
| формуле
А. Шиффеля
| формуле Кунце для сосны q2─0,20;
для ели q2─0,21
|
| q0=D0/D1,3=29,9/27,2=1,10
q0=26,4/25,2=1,05
| q1=D1/4H/D1,3=22,8/27,2=0,84
q1=22,1/25,2=0,88
| q2=D1/2H/D1,3=18,8/27,2=0,69
q2=18,4/25,2=0,73
| q3=D3/4H/D1,3=11,9/27,2=0,44
q3=11,6/25,2=0,46
| f=Vc/Vц= 0,6678/(0,0581*24,4)=0,471
| f=q22=0,476
| f=0,477
| f=0,66q22+0,32/q2H+0,14= =0,473
| f=q2-0,20=0,490
(для сосны)
|
| Расхождение с точным видовым числом в процентах
|
| +1,1
| +1,3
| +0,4
| +4,0
|
| | | | | | | | | | |
 Пример выполнения задания 4 Т а б л и ц а 6
Пример выполнения задания 4 Т а б л и ц а 6
Структура формул, по которым рассчитываются видовые числа, предполагает наличие достаточно тесной корреляционной зависимости между  , а следовательно, между сбегом и видовым числом. Поэтому видовое число является интегрирующим показателем формы ствола и обоснованно используется в качестве объемообразующего параметра в формуле V ст = GHƒ.
, а следовательно, между сбегом и видовым числом. Поэтому видовое число является интегрирующим показателем формы ствола и обоснованно используется в качестве объемообразующего параметра в формуле V ст = GHƒ.
где G – площадь сечения на высоте 1,3 м от основания ствола, м2;
H – высота ствола, м;
ƒ;– видовое число.
Студенты вычерчивают схемы ствола, где показывают все измерения, необходимые для последующих расчетов. Коэффициенты формы вычисляют в коре и без коры, а видовые числа только в коре.
Видовое число, найденное как отношение объема ствола к объему цилиндра, наиболее точное и принимается за истинное значение, а все остальные сравниваются с ним. На основе полученных расхождений в процентах студент делает вывод о степени точности различных способов определения видового числа и устанавливает причину разной точности этих способов.
Коэффициенты формы вычисляются с точностью до 0,01, а видовые числа до 0,001.




 ,
,

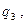
 - коэффициенты формы,
- коэффициенты формы,  - диаметры соответственно на нулевой высоте ствола, на высоте груди, на четвертой части высоты ствола, на половине высоты и на трех четвертях высоты.
- диаметры соответственно на нулевой высоте ствола, на высоте груди, на четвертой части высоты ствола, на половине высоты и на трех четвертях высоты. Каждый коэффициент в отдельности характеризует сбег той части ствола, к которой он относится. Взятые вместе они достаточно точно позволяют судить о форме всего ствола, степени его сбежистости, объеме, характере и размере лесоматериалов, которые можно получить из ствола.
Каждый коэффициент в отдельности характеризует сбег той части ствола, к которой он относится. Взятые вместе они достаточно точно позволяют судить о форме всего ствола, степени его сбежистости, объеме, характере и размере лесоматериалов, которые можно получить из ствола. он, в частности, используется при расчете другого показателя формы ствола, который получил название видового числа. Первые исследователи в поисках обобщающего показателя формы ствола пришли к единому мнению, что сравнение объема ствола с объемом цилиндра, имеющего с ним одинаковую высоту и площадь основания, равную площади сечения на высоте груди, хорошо описывает степень приближения объема ствола к объему такого цилиндра. Установленное таким способом видовое число получило название старого видового числа:
он, в частности, используется при расчете другого показателя формы ствола, который получил название видового числа. Первые исследователи в поисках обобщающего показателя формы ствола пришли к единому мнению, что сравнение объема ствола с объемом цилиндра, имеющего с ним одинаковую высоту и площадь основания, равную площади сечения на высоте груди, хорошо описывает степень приближения объема ствола к объему такого цилиндра. Установленное таким способом видовое число получило название старого видового числа: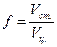 ,
,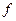 – видовое число (старое в данном случае),
– видовое число (старое в данном случае),  – объемы ствола и цилиндра. Старое видовое число дает качественную характеристику формы ствола, получившую название полнодревесность:чем больше видовое число, тем в большей степени объем ствола приближается к объему цилиндра, то есть тем более ствол полнодревесен, и наоборот. Точность расчета видового числа по приведенной формуле зависит от точности определения объема ствола. Более поздние исследования обосновали расчеты видовых чисел на иных зависимостях:
– объемы ствола и цилиндра. Старое видовое число дает качественную характеристику формы ствола, получившую название полнодревесность:чем больше видовое число, тем в большей степени объем ствола приближается к объему цилиндра, то есть тем более ствол полнодревесен, и наоборот. Точность расчета видового числа по приведенной формуле зависит от точности определения объема ствола. Более поздние исследования обосновали расчеты видовых чисел на иных зависимостях:  – этот способ основан на определении объема по простой формуле через срединное сечение ствола, поэтому дает невысокую точность; хорошую точность (
– этот способ основан на определении объема по простой формуле через срединное сечение ствола, поэтому дает невысокую точность; хорошую точность ( 3 %) определения видового числа дает формула Шиффеля:
3 %) определения видового числа дает формула Шиффеля: .
. – 0,20, для ели
– 0,20, для ели  .
. и
и  , позволили сформулировать закон, согласно которому стволы всех древесных пород, растущих в насаждениях, в любых условиях, при равной высоте, диаметре и коэффициенте формы, имеют почти равные видовые числа, а следовательно, и объемы.
, позволили сформулировать закон, согласно которому стволы всех древесных пород, растущих в насаждениях, в любых условиях, при равной высоте, диаметре и коэффициенте формы, имеют почти равные видовые числа, а следовательно, и объемы. Пример выполнения задания 4 Т а б л и ц а 6
Пример выполнения задания 4 Т а б л и ц а 6
 , а следовательно, между сбегом и видовым числом. Поэтому видовое число является интегрирующим показателем формы ствола и обоснованно используется в качестве объемообразующего параметра в формуле V ст = GHƒ.
, а следовательно, между сбегом и видовым числом. Поэтому видовое число является интегрирующим показателем формы ствола и обоснованно используется в качестве объемообразующего параметра в формуле V ст = GHƒ.


