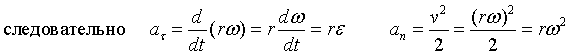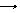Первый закон Ньютона
Если даже пришлось пропустить пробежку потому, что не нашлось времени или сил, не вините себя и ни в коем случае не используйте это как оправдание. Не стоит поднимать белый флаг и сдаваться, ведь в жизни бывает всякое. Забудьте о пропущенном дне и двигайтесь дальше. Кстати, этот совет можно отнести к любому начинанию.
Вопросы к экзамену по физике географам 1 сессия 1. Механическое движение. Системы отсчета. Механическое движение – это процесс изменения положения данного тела в пространстве с течением времени относительно другого тела, которое мы считаем неподвижным. Тело, условно принятое за неподвижное – тело отсчета. Тело отсчета – это тело, относительно которого опре-деляется положение другого тела. Обычно в качестве тела отсчета выбирается земля, но может быть и движущийся относительно земли предмет: автомобиль, лодка, самолет и т.д.
Рис. 1. Пример. Автомобиль (рис. 1) движется относительно тела отсчета – дерева. Человек вместе с автомобилем движется относительно этого тела отсчета, но относительно другого тела отсчета (автомобиль) находится в покое. Механическое движение всегда относительное. Механический покой всегда относительный. Система отсчета – это тело отсчета, система координат, жестко связанная с ним, и прибор для измерения времени движения. Простейшей системой координат является прямоугольная декартова система (рис. 2). Система координат нужна для определения положения тела относительно тела отсчета. Выбор системы отсчета зависит от условий дан-ной задачи.
Рис. 2. Движение реальных тел, как правило, сложное. Для упрощения рас-смотрения движений пользуются моделями. Одними из первых моделей реальных тел являются абсолютное твердое тело и материальная точка. Абсолютно твердым телом называется тело, рас-стояние между любыми двумя точками которого остается постоянным при любых внешних воздействиях. Эта модель позволяет исключить деформацию тел при движении. Изу-чив движение абсолютно твердого тела, мы понимаем закономерности движения реальных твердых тел. Простейшими видами механического движения абсолютно твердого тела являются поступательное (рис. 3) и вращательное (рис. 4).
Рис. 3
Рис. 4 Поступательным движением называется движение, при котором любая прямая, соединяющая две произ-вольные точки тела, перемещается параллельно самой себе. При поступательном движении траектории всех точек тела одинаковы. Таким образом, для описания поступательного движения тела достаточно описать движение какой-либо одной его точки (т.е. рассмотреть кинематику прямолинейного движения материальной точки). Вращательным движением называется такое движе-ние, при котором все точки тела описывают окружности в параллельных плоскостях, а центры этих окружностей лежат на одной прямой, называемой осью вращения (неподвижная ось – рис. 3). Любое плоское движение можно представить как результат поступательного движения вдоль ВВ' и «чистого вращения» на угол А'В'А'' – рис. 4. Изучая характер движения Земли, планет относительно Солнца, мы можем не учитывать размеры этих тел и считать их материальными точками (т.е. рассмотреть кинематику криволинейного движения материальной точки). Материальной точкой называется тело, размерами и формой которого можно пренебречь в данной задаче. Данное понятие является математической абстракцией. Одно и то же тело в одних задачах можно рассматривать как материальную точку, а в других задачах – нельзя. Например, радиус Земли RЗемли равен 6400 км, расстояние между Солнцем и Землей L равно 150 000 000 км (L >> RЗемли). Рассматривая движение Земли относительно Солнца, радиусом Земли можно пре-небречь и считать, что Земля – материальная точка. Однако если нужно выяснить причины смены времен года, то Землю уже нельзя считать матери-альной точкой, а надо учитывать ее размеры, вращение вокруг оси и т.д. Мы будем изучать механическое движение материальной точки для того, чтобы потом определить движение реального тела.
2. Кинематика поступательного движения точки. Траектория движения. Перемещение. Скорость. Ускорение. При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки. Основные характеристики движения материальной точки: траектория движения, перемещение точки, пройденный ею путь, координаты, скорость и ускорение. Линию, по которой движется материальная точка в пространстве, называют траекторией. Перемещением материальной точки за некоторый промежуток времени называется вектор перемещения ∆r=r-r0, направленный от положения точки в начальный момент времени к ее положению в конечный момент. Скорость материальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета. Вектор ускорения характеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета.
3. Кинематика вращательного движения. Угловая скорость. Угловое ускорение. Если в процессе движения абсолютно твердого тела (рис.2.1) его точки А и В остаются неподвижными, то и любая точка С тела, находящаяся на прямой АВ, также должна оставаться неподвижной. В противном случае расстояния АС и ВС должны были бы изменяться, что противоречило бы предположению об абсолютной твердости тела. Поэтому движение твердого тела, при котором две его точки Аи В остаются неподвижными, называют вращением тела вокруг неподвижной оси, а неподвижную прямую АВ называют осью вращения.
Рассмотрим произвольную точку М тела, не лежащую на оси вращения АВ. При вращении твердого тела расстояния М А и МВ и расстояние ρ; точки М до оси вращения должны оставаться неизменными. Таким образом, все точки тела, вращающегося вокруг неподвижной оси, описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны этой оси. Движение абсолютно твердого тела, закрепленного в одной неподвижной точке, называют вращением тела вокруг неподвижной точки - центра вращения. Такое движение абсолютно твердого тела в каждый момент времени можно рассматривать как вращение вокруг некоторой оси, проходящей через центр вращения и называемой мгновенной осью вращения тела. Положение мгновенной оси относительно неподвижной системы отсчета и самого тела с течением времени может изменяться. Угловая скорость. векторная величина
называется угловой скоростью тела. Вектор
т.е. при равномерном вращении
Угловое ускорение. В случае неравномерного движения
В случае вращения тела вокруг
4. Тангенциальное, нормальное, полное ускорение. Связь между линейным и угловым ускорением. По определению:
Следовательно
Связь между линейной и угловой скоростью и ускорением.
Отдельные точки вращающегося тела имеют различные линейные скорости v, которые непрерывно изменяют свое направление и зависят от ω и расстояния r соответствующей точке до оси вращения. Точка, находящаяся на расстоянии r от оси вращения проходит путь Δ S = r Δφ.
Поделим обе части равенства на Δ t:
Но Таким образом, чем дальше отстоит точка от оси вращения, тем больше ее линейная скорость. Известно, что
Откуда
Из написанных формул видно, что a τ, a n и a растут с увеличением расстояния точек до оси вращения. Формула v = ω r устанавливает связь между модулями векторов v, r, и ω, которые перпендикулярны друг к другу.
Т.к. ω | r,то можно написать v = ω∙ r ∙ sina это ничто иное как модуль векторного произведения. Таким образом v = [ ω r ] Рассмотренные простейшие виды движения твердого тела важны потому, что любое движение твердого тела сводится к ним.
5. Три закона Ньютона. Сила. Масса. Первый закон Ньютона Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.
|



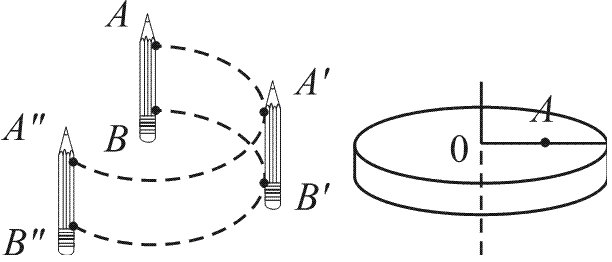


 направлен вдоль мгновенной оси вращения в сторону, определяемую правилом винта, т.е. также как вектор элементарного поворота
направлен вдоль мгновенной оси вращения в сторону, определяемую правилом винта, т.е. также как вектор элементарного поворота  . Модуль вектора угловой скорости равен
. Модуль вектора угловой скорости равен 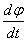 . Вращение с постоянной угловой скоростью называется равномерным, при этом:
. Вращение с постоянной угловой скоростью называется равномерным, при этом:
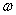 показывает, на какой угол поворачивается тело за единицу времени.
показывает, на какой угол поворачивается тело за единицу времени. не остается постоянной. Величина, характеризующая скорость изменения угловой скорости называется угловым ускорением и равна:
не остается постоянной. Величина, характеризующая скорость изменения угловой скорости называется угловым ускорением и равна:
 углового ускорения направлен вдоль оси вращения в ту же сторону, что и
углового ускорения направлен вдоль оси вращения в ту же сторону, что и  и при замедленном
и при замедленном  в обратном направлении. (рис 2.3 а),б))
в обратном направлении. (рис 2.3 а),б)) Тангенциальное ускорение характеризует быстроту изменения скорости движения по численному значению и направлена по касательной к траектории.
Тангенциальное ускорение характеризует быстроту изменения скорости движения по численному значению и направлена по касательной к траектории.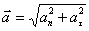 Нормальное ускорение характеризует быстроту изменения скорости по направлению.
Нормальное ускорение характеризует быстроту изменения скорости по направлению.

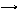


 , при Δ t 0 получим пределы от левой и правой частей равенства:
, при Δ t 0 получим пределы от левой и правой частей равенства: