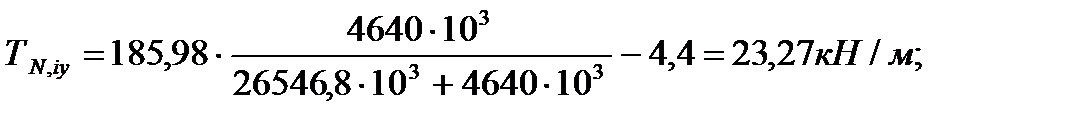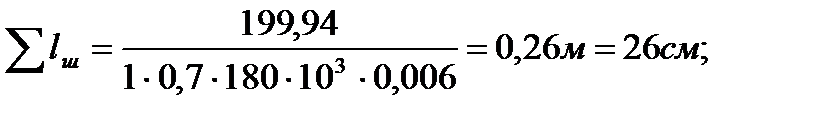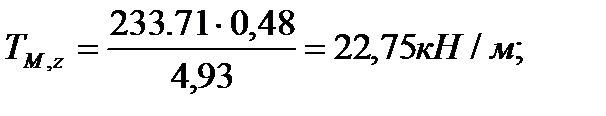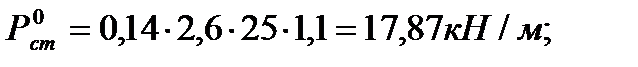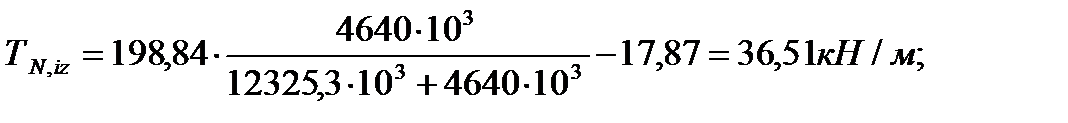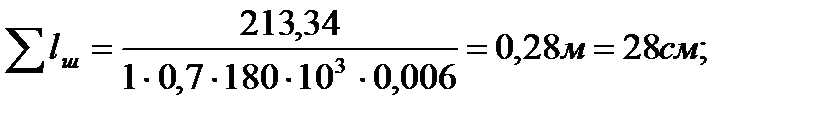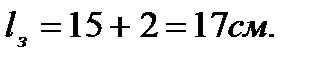В рамках системного подхода при решении задачи синтеза
4.3.1. Сбор нагрузок Привязка колонн в здании центральная. Стены из кирпича глиняного одинарного (ГОСТ 530-95) толщиной 540 мм. Колонны сечением 400х400 мм. Класс бетона (класс арматуры): - для диафрагм жесткости В12,5 (Вр-I); - для колонн В30 (AIII); - для ригелей В25 (AIII).
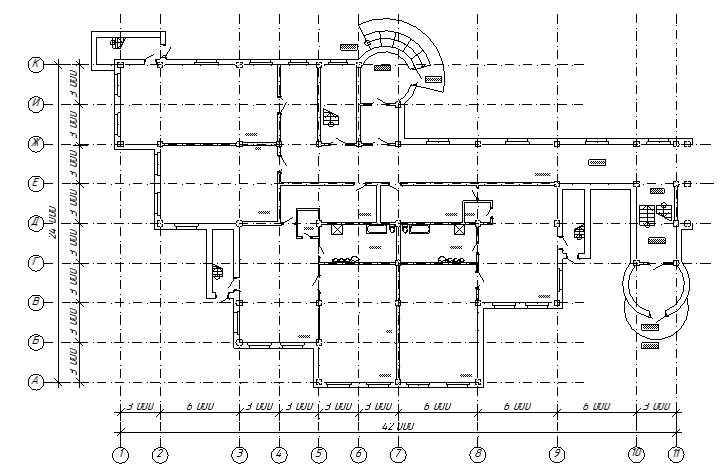
Рис. 1. План типового этажа. Сбор нагрузок на 1 м2 перекрытии Таблица №3.
Сбор нагрузок на 1 м2 покрытия. Таблица 2.
Нагрузка от стен Нагрузка от стен со стороны главного фасад, на первом этаже.
l1=6 м – длина пролёта; hэт=3,6 м – высота этажа; lок=1,8 м – длина окна; hок=1,8 м – высота окна; ρст=1,8 кН/м2 – плотность стены; rок=0,2 кН/м2 – плотность стекла; gf1=1,1; gf2=1,3 – коэффициенты надёжности.
Нагрузка от стен с торцевой стороны, на первом этаже.
Ветровая нагрузка на здание. Ветровая нагрузка для многоэтажных зданий регулярной структуры в произвольной точке по высоте здания определяется по формуле:
k – коэффициент, учитывающий изменение скоростного напора по высоте в зависимости от типа местности. Тип местности С. kн – коэффициент, учитывающий изменение скоростного напора на уровне верха здания. К из таблицы 6 СНиП 2.01.07-85*.
Vн – коэффициент пульсации ветра, определяется на отметке верха здания по таблице 7 СНиП 2.01.07-85* в зависимости от типа местности; zн=1,78 при z5=9,3. n - коэффициент пространственной корреляции ветрового давления, которое определяется в зависимости от размера здания (таблица 9 СНиП 2.01.07-85). L1=42,68м.: n5=0,71, n9,3=0,71. L2=24,68м.: n5=0,85, n9,3=0,84. Высота здания: t – высотный параметр, определяется по формуле: zi – расстояние от уровня земли до рассматриваемого уровня.
x - коэффициент динамичности, позволяющий рассматривать динамическую нагрузку как статическую, определяется в зависимости от параметра e по графику 2 СНиП 2.01.07-85*.
В зависимости от e и логарифмического декремента d=0,1, получим x=1,1. Расчётная нагрузка, распределённая по высоте фасада, определяется по формуле: Для главного фасада: L1=42,68м.
Для торцевой стены: L2=24,68м.
При расчёте сложных многоэтажных систем фактическую ветровую нагрузку приводят к эквивалентной трапеции, таким образом, чтобы площади нормативной и приведенной фигур были одинаковыми и центр тяжести обеих фигур располагался на одном уровне Х0.
S – статический момент инерции фактической фигуры относительно земли; А – площадь фактической фигуры.
Рис.2. Эпюры ветрового давления. Для главного фасада:
Для торцевой стороны:
Параметры эквивалентной трапеции определяются следующим образом:
Для фасада:
Для торцевой стороны:
При трапециевидной эпюре для любого уровня по высоте здания получается погонная ветровая нагрузка: Консольная ветровая сила: Консольный изгибающий момент: х – координата горизонтального уровня, отсчитываемого от верха здания. 4.3.2. Предварительный расчет количества диафрагм Количество диафрагм параллельных соответствующей оси, вычисляется по формуле: My(z) – изгибающий момент от внешней нагрузки, действующий на целостную пространственную несущую систему в плоскости YOX или ZOX.
q – интенсивность ветровой нагрузки в уровне верха здания; Для предварительного расчета x=H=9,3 м. kвн=1,2 – коэффициент, учитывающий внецентренное приложение вертикальной нагрузки; åР – суммарная вертикальная нагрузка с учетом веса конструкций и временных нагрузок, собранная со всех этажей в пределах плана здания.
yn3=0,64 – коэффициент, который зависит от количества этажей; n=2 – количество этажей; n1*=10 и n2*=8 – количество ячеек стен по периметру здания; Nст,1эт – нагрузка от стеновых панелей; Мпр – предельный изгибающий момент, воспринимающий горизонтальное сечение одной плоской диафрагмы
В – изгибная жесткость диафрагмы с учетом податливости связей сдвига, определяется в направлении большей жесткости
kdef – коэффициент условия работы связей сдвига,
c - коэффициент, учитывающий податливость горизонтальных швов
h2=0,01 – суммарная высота растворных швов в пределах первого этажа;
Ев1=19×103 МПа – модуль упругости стенки диафрагмы жесткости, бетон тяжелый В12,5, подвергнутый тепловой обработке; Ев2=22×103 МПа – модуль упругости бетона шва, бетон мелкозернистый В-20, естественного твердения; Ав1=Ав2 – площадь соответственно диафрагмы жесткости и растворного шва; J – момент инерции диафрагмы относительно оси 1-1(см. рис. 5).
Изгибная жесткость диафрагмы:
Предельно допустимый момент:
Относительно оси Y:
Количество диафрагм относительно оси Y:
J – момент инерции диафрагмы относительно оси 2-2(см. рис. 5).
Изгибная жесткость диафрагмы:
Предельно допустимый момент:
Относительно оси Z:
Рис.3. Расположение диафрагм жесткости в здании. Вычисляем жесткость диафрагмы с учетом колонн:
4.3.3. Определение вертикальных нагрузок, действующих на диафрагму Определение центра жесткости здания. Определяем положение центра жёсткости здания относительно проходящих через центр плана фиктивных осей Z,Y.
Рис.4. Вертикальные нагрузки на диафрагму. Рассмотрим диафрагмы расположенных вдоль оси Y и оси Z с одинаковыми грузовыми площадями. Диафрагмы Д1.
Рис.5. Нагрузка на диафрагмы Д1.
Нагрузка от перекрытия.
ql, qsh – длительная и кратковременная нагрузка
yl, ysh – коэффициенты сочетания для длительной и кратковременной нагрузок для второго основного сочетания;
Нагрузка от покрытия.
Погонная вертикальная нагрузка, приходящаяся на
Рd1 – собственный вес диафрагмы с колоннами в пределах 1-го этажа,
Эквивалентный погонный момент:
Общий эксцентриситет приложения нагрузки:
Диафрагмы Д2.
Рис.6. Нагрузка на диафрагмы Д2.
Нагрузка от перекрытия.
Нагрузка от покрытия.
Погонная вертикальная нагрузка, приходящаяся на диафрагму Д2
Эквивалентный погонный момент:
Общий эксцентриситет приложения нагрузки:
4.3.4. Учёт влияния продольного изгиба на усилие диафрагмовой системы и её деформации Под действием вертикальных внецентренно приложенных нагрузок прогибы элементов диафрагмовой системы увеличиваются, возрастают начальные эксцентриситеты приложения нагрузок, и это приводит к увеличению результирующего момента, поперечной силы и горизонтальной деформации. Эффективность продольного изгиба увеличивается коэффициентами продольного изгиба h.
ny(z), nq - безразмерные величины вертикальной нагрузки, действующей на всю диафрагмовую систему и отвечающую за изгиб и кручение здания. Они зависят от высоты вертикальной суммарной действующей нагрузки и полной жёсткости здания.
Вiy(z) – изгибная жёсткость поперечных или продольных диафрагм; zi, yi – координаты центра тяжести Вw - жёсткость диафрагмовой системы на кручение при изгибе
ncr,y(z), ncr,q - критическое значение безразмерного параметра вертикальной нагрузки, приводящей к потери устойчивости здания;
4.3.5. Расчет диафрагмовой системы на вертикальные нагрузки Расчёт выполняется для 2-х диафрагм Д2(Д1,Д5,Д6) и Д3(Д4). Изгибающий момент в продольном сечении диафрагмы, вызванный действием внецентренно приложенных вертикальных нагрузок с учётом закручивания здания. Поперечная сила: Продольная сила: Параллельно оси Y:
х=H=9,3 м; T – Равнодействующий бимомент в пространственной несущей системе от внецентренно приложенных нагрузок,
Параллельно оси Z:
4.3.6. Горизонтальные нагрузки и определение усилия в диафрагме Горизонтальная распределённая нагрузка на торец диафрагмы с учётом кручения здания определяется по формуле:
еi - координата смещения центра жесткости здания или эксцентриситет приложения ветровой нагрузки. Момент от горизонтальных нагрузок: Поперечная сила от горизонтальных нагрузок: В результате статического расчёта на совместное действие вертикальных и горизонтальных нагрузок определяется распределённый момент между диафрагмами, а так же поперечные и продольные силы.
Относительно оси Y:
Относительно оси Z:
4.3.7. Распределение усилий между стенками колонны и диафрагмы Усилие, приходящееся на колонну:
Усилие, приходящееся на стенку диафрагмы:
N – полное усилие, действующее на диафрагму;
Ев,к=29×103 МПа – модуль упругости бетона марки В30 для колонны;
Ев,с=19×103 МПа – модуль упругости бетона марки В14,5 для стенки диафрагмы;
4.3.8. Расчет стенки диафрагмы Стенка диафрагмы рассчитывается на усилия от полной нагрузки Nст,N и от нагрузки длительного действия Nст.,N l с учетом эксцентриситета приложения нагрузки
Ny, Nz – соответственно продольные силы, которые могут выдержать горизонтальные сечения элемента в случае их приложения с эксцентриситетом ey, ez.
a=1 – коэффициент, учитывающий вид бетона; Rb=7,5 МПа – расчетное сопротивление бетона для стенки диафрагмы; Авy, Aвz – соответственно площади сжатой зоны бетона для загружения с ey и ez.
Параллельно оси Y: Параллельно оси Z: где Ncr – критическая сжимающая сила, приводящая к потере устойчивости элемента.
Ев=19,0×103 МПа – модуль упругости стенки диафрагмы; Jy=Jz – момент инерции сечения относительно оси Y и Z.
j l – коэффициент, учитывающий длительность действия нагрузки. Параллельно оси Y: Параллельно оси Z: d l – относительный эксцентриситет
Nc – предельное усилие в стенке при центральном сжатии
Относительно оси Y:
Принимаем d l = 0,29 м.
Условие выполнено, площадь арматуры подбираем конструктивно.
Так как l=38,30, то mmin=0,002. Площадь арматуры: Принимаем 160 Æ 5 Вр-I с Аs=31,36 см2. Относительно оси Z:
Принимаем d l=0,18 м.
Условие выполнено, площадь арматуры подбираем конструктивно.
Так как l=59,02, то mmin=0,002. Площадь арматуры: Принимаем 110 Æ 4 Вр-I с Аs=13,86 см2. 4.3.9. Расчет горизонтального шва на срез
bk=hk=0,4 м; Qiy(x) – поперечная сила от расчетных нагрузок в опорном сечении диафрагмы и от вертикальных и горизонтальных нагрузок; Ni(x) – расчетная вертикальная сила, приходящаяся на эту же диафрагму в этом же сечении; Rb,t=1,2 МПа – расчетное сопротивление бетона на растяжение класса В30 для колонны. Опасные сечения на срез: 1. при х=H=9,3 м; 2. при х=hэт=3,6 м. 1). При х=9,3 м. ·
·
2). При х=3,6 м. ·
·
4.3.10. Расчёт прочности по наклонному сечению Первоначально предполагаем, что стержни по расчету не требуются, то есть прочность обеспечивается бетоном. Поэтому проверку выполняем по следующей формуле:
jn – коэффициент, учитывающий обжатие бетона под нагрузкой Ni.
с – проекция наклонной трещины на продольную ось элемента,
qm – средняя величина нагрузки в пределах этажа.
Относительно оси Y:
Так как условие сошлось, то расчет стержней не требуется. Они принимаются конструктивно из условия сварки с продольными стержнями при этом шаг стержней S£ 500 мм. Относительно оси Z:
Так как условие сошлось, то расчет стержней не требуется. Они принимаются конструктивно из условия сварки с продольными стержнями при этом шаг стержней S£ 500 мм. 4.3.11. Расчет креплений, соединяющих стенку диафрагмы и колонну Колонна и стенка диафрагмы воспринимают нагрузку совместно, поэтому по вертикальным швам, соединяющим колонны и стенку, возникают, перерезывающая сила Т. Эта сила складывается из двух составляющих:
Р0i – погонная нагрузка на рассматриваемую диафрагму; Р0к – погонная вертикальная нагрузка, приложенная непосредственно к колонне;
Р0с – погонная вертикальная нагрузка, приложенная непосредственно к стенке диафрагмы;
gf=1,1; rж/б=25кН/м3. Под действием изгибающего момента в швах возникают произвольная дополнительная перерезывающая сила
Qiy – расчетная поперечная сила, приходящаяся на рассматриваемую диафрагму от вертикальных и горизонтальных нагрузок; Jred – момент инерции всей диафрагмы с учетом колонн, Sk – статический момент инерции сечения одной колонны относительно центра тяжести диафрагмы,
Полное сдвигающее усилие, действующее в шве в пределах одного этажа:
Суммарная длина сварного шва соединения колонны со стенкой:
nw=1 – количество швов; Электрод Э42: b=0,7; Rw=180 МПа; Kf=6 мм. Расчет шва, приходящегося на одну закладную деталь:
nз – количество закладных деталей, min 2. Размер закладной детали: Относительно оси Y:
Относительно оси Z:
В рамках системного подхода при решении задачи синтеза обычно руководствуются следующими принципами и приемами: 1. Сочетание декомпозиции, композиции и иерархичности. 2. Выделение нескольких этапов создания системы, фиксирующих переход на новый уровень рассмотрения. 3. Всестороннее рассмотрение взаимодействия системы с элемента- ми внешней среды. 4. Всестороннее рассмотрение основных видов взаимодействия внутри системы между ее элементами. 5. Сочетание различных качественных и количественных методов исследования. 6.Генетический анализ и учет предыстории развития данного класса систем 7. Учет возможности изменения исходных данных и даже содержа- ния решаемой задачи в ходе многоэтапного процесса создания системы.
Перечисленные принципы и подходы составляют основу эволюционной технологической схемы процесса реального синтеза сложной
|

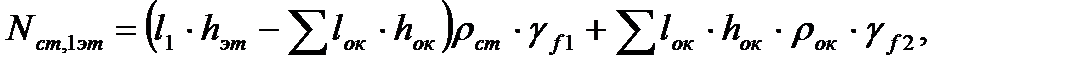 где
где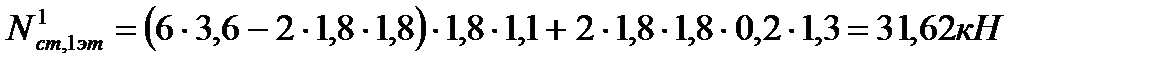 .
.
 , где
, где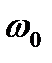 =0,23 кПа – нормативное значение ветрового давления для I ветрового района
=0,23 кПа – нормативное значение ветрового давления для I ветрового района - аэродинамический коэффициент
- аэродинамический коэффициент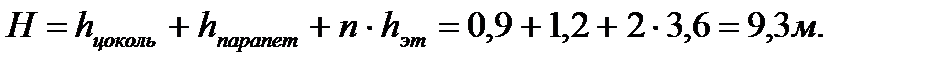
 , где
, где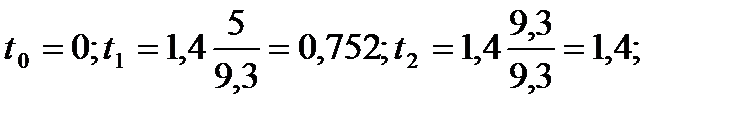
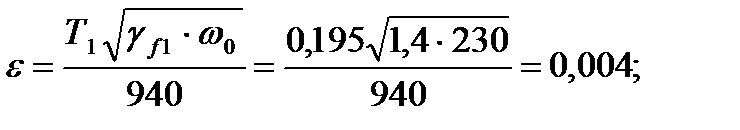 где:
где: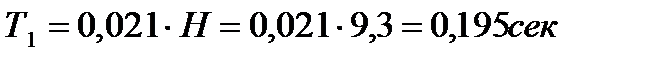 период собственных колебаний первой формы.
период собственных колебаний первой формы.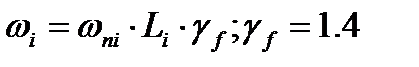
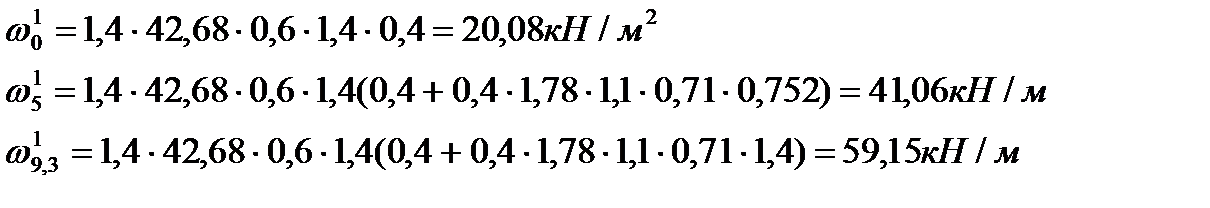
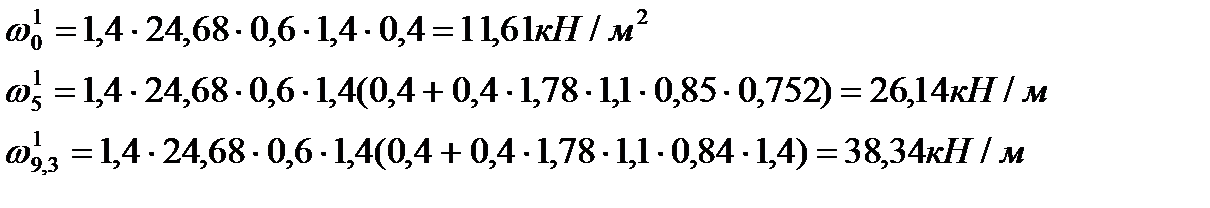
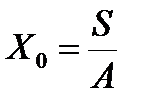 ,где
,где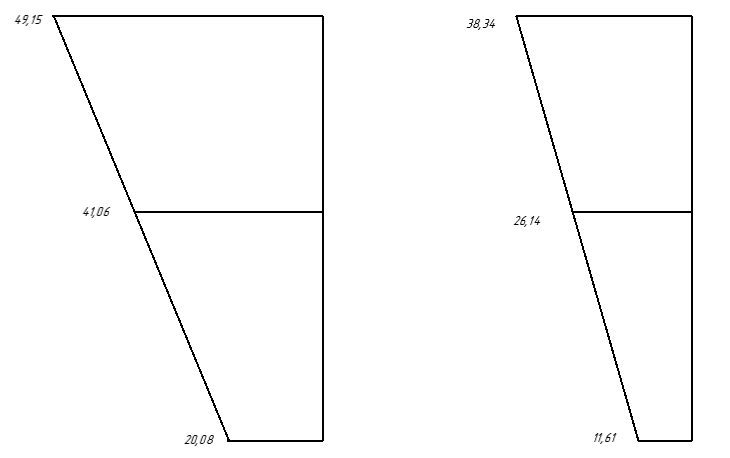
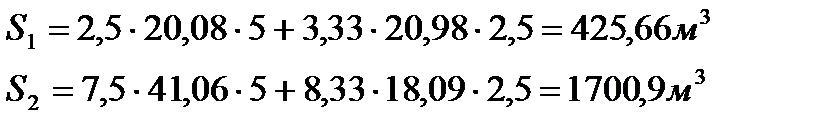

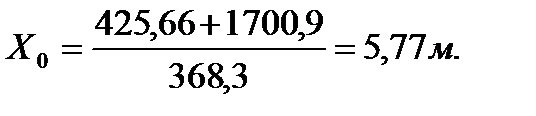
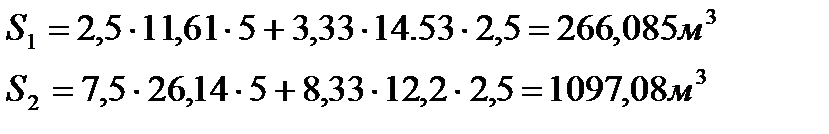

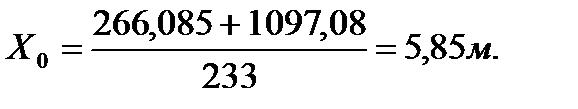
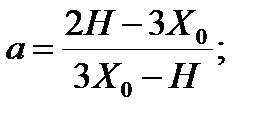

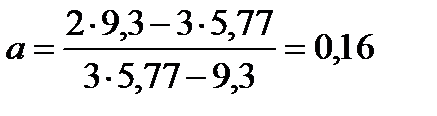



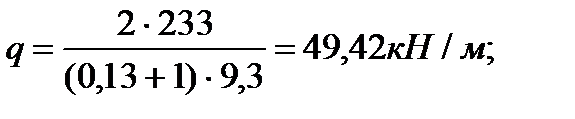
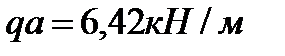
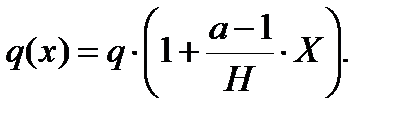
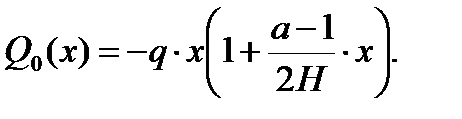
 где
где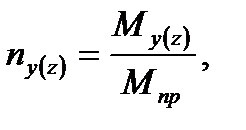 где
где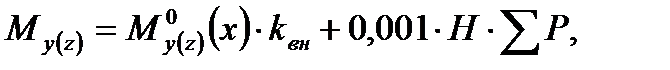 где
где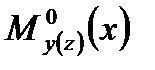 - консольный изгибающий момент, действующий на всю несущую систему в соответствующей плоскости от горизонтальной нагрузки;
- консольный изгибающий момент, действующий на всю несущую систему в соответствующей плоскости от горизонтальной нагрузки;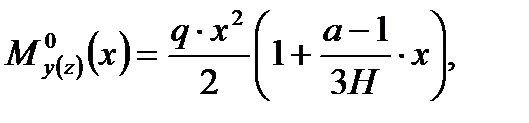 где
где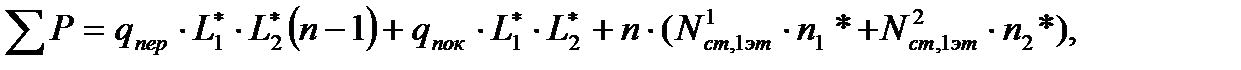 где
где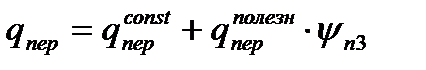 - полная расчетная нагрузка на перекрытие здания в плане;
- полная расчетная нагрузка на перекрытие здания в плане;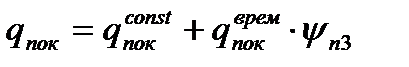 - полная расчетная нагрузка на покрытие здания в плане;
- полная расчетная нагрузка на покрытие здания в плане;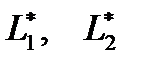 - размеры здания в плане;
- размеры здания в плане; где
где где
где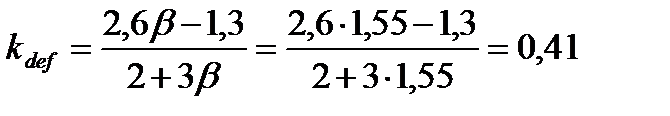 ,где
,где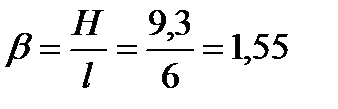 - относительная высота столба диафрагмы;
- относительная высота столба диафрагмы; ,где
,где 
 - высота стенки диафрагмы в пределах этажа;
- высота стенки диафрагмы в пределах этажа; где
где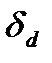 -толщина стенки диафрагмы.
-толщина стенки диафрагмы. 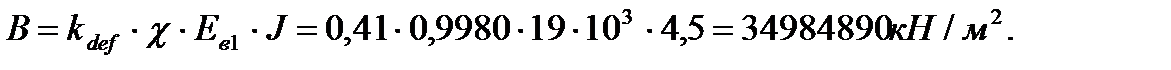
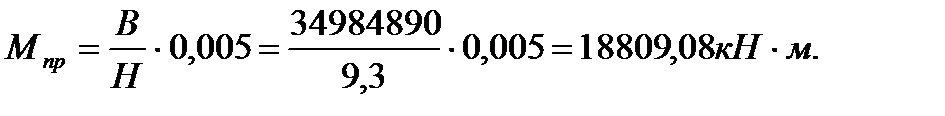
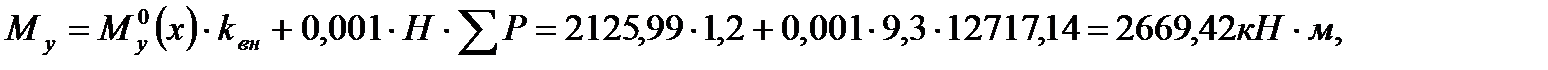 где
где
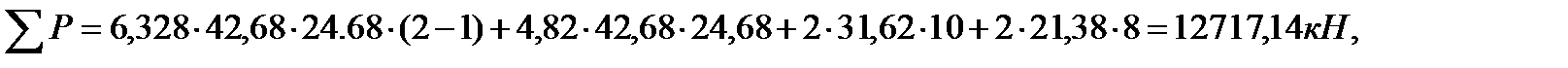 где
где
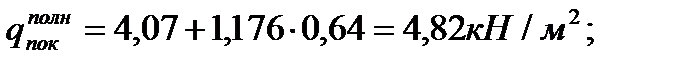
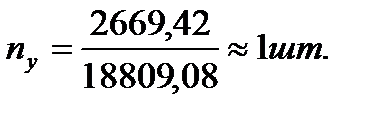 Примем ny=1 шт.
Примем ny=1 шт. где
где
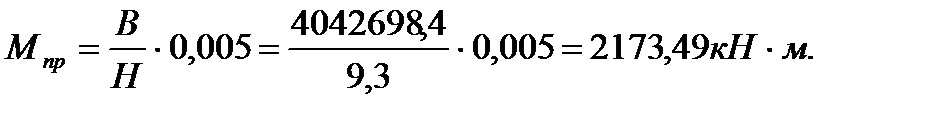

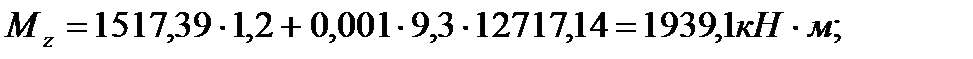
 Примем nz=1 шт.
Примем nz=1 шт.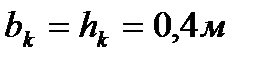 ;
;
 ;
;
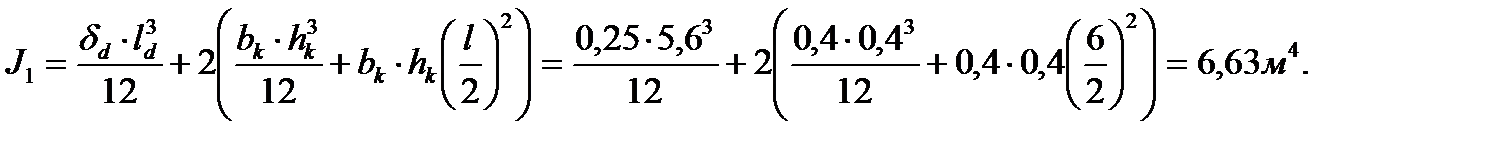

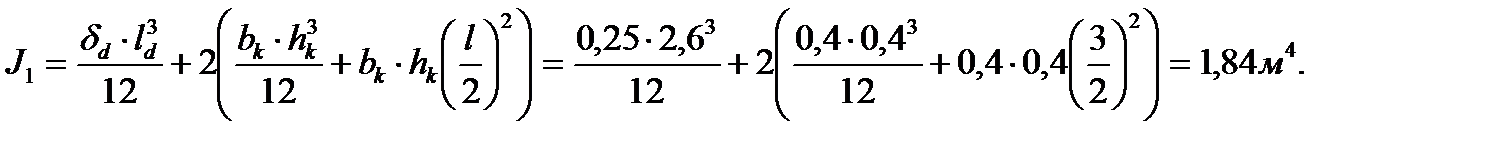
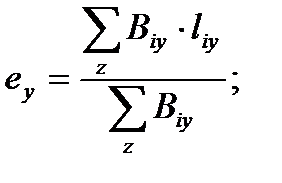
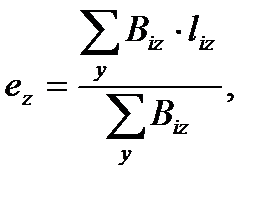 где
где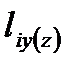 - расстояние между центром тяжести сечения
- расстояние между центром тяжести сечения  -ой диафрагмы параллельно оси Y или Z до геометрического центра плана вдоль оси Y или Z;
-ой диафрагмы параллельно оси Y или Z до геометрического центра плана вдоль оси Y или Z;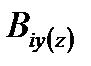 - изгибная жесткость
- изгибная жесткость  -ой диафрагмы относительно оси Y или Z;
-ой диафрагмы относительно оси Y или Z;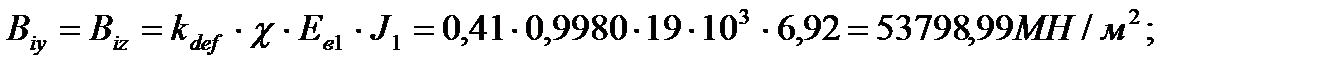

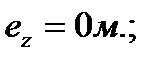
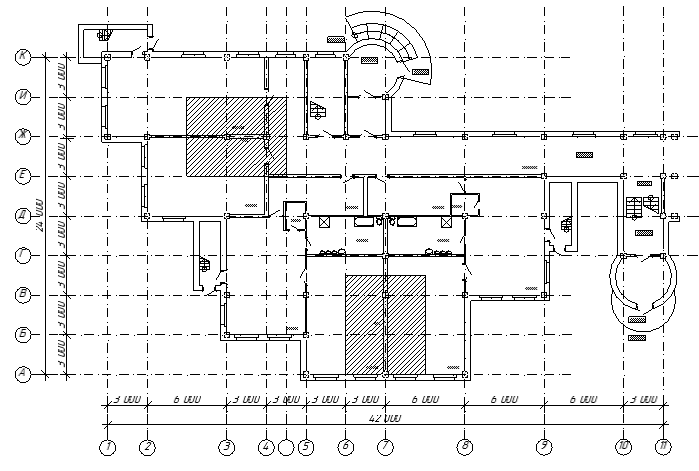


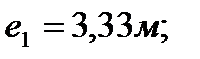
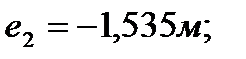


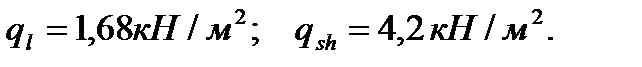
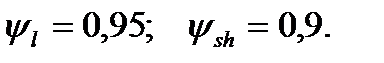
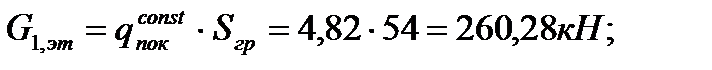
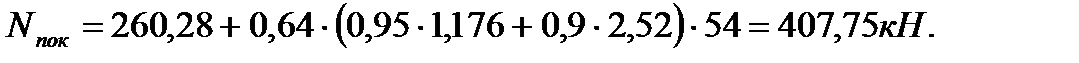
 -ую диафрагму.
-ую диафрагму. где
где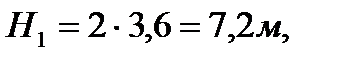
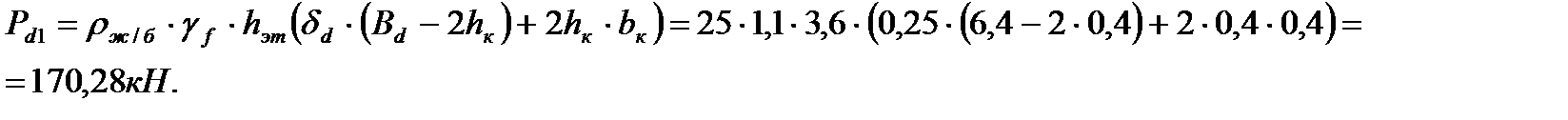 Погонная вертикальная нагрузка, приходящаяся на диафрагму Д1.
Погонная вертикальная нагрузка, приходящаяся на диафрагму Д1.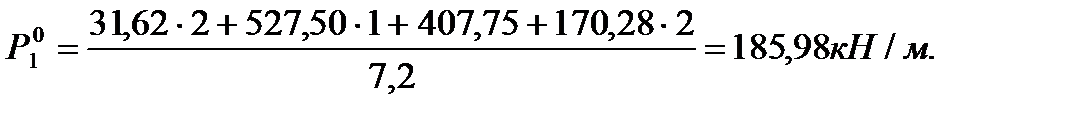
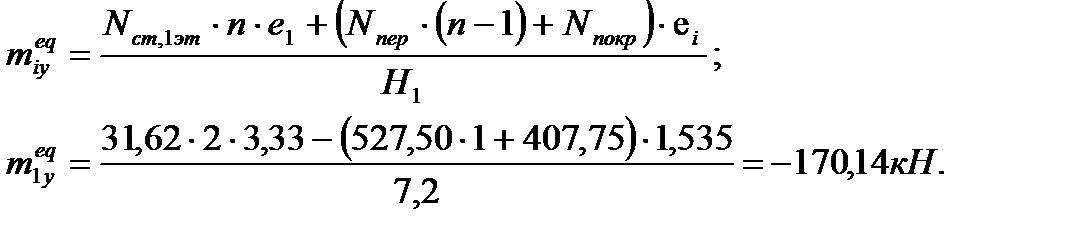
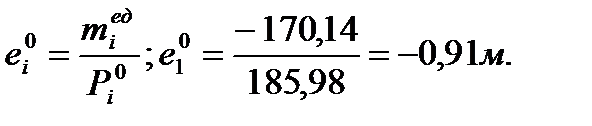

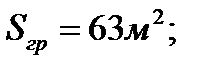
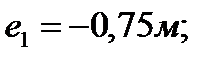
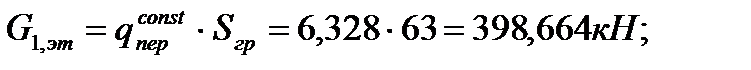
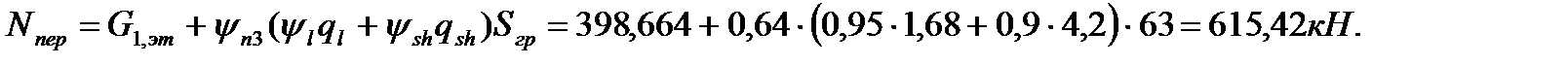
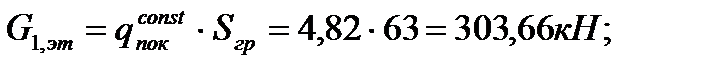

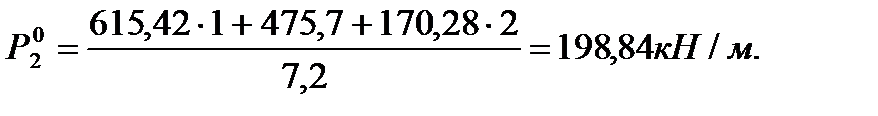
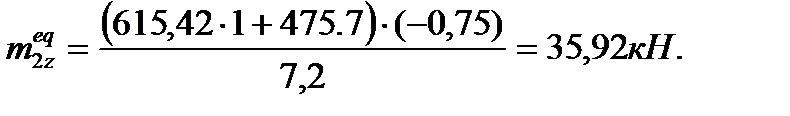

 - коэффициент, учитывающий увеличение изгибающего момента;
- коэффициент, учитывающий увеличение изгибающего момента; - коэффициент, учитывающий увеличение крутящего момента или бимомента;
- коэффициент, учитывающий увеличение крутящего момента или бимомента;
 где
где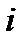 -ой диафрагмы;
-ой диафрагмы;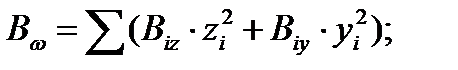

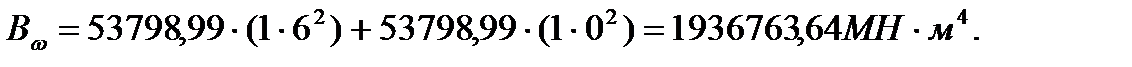
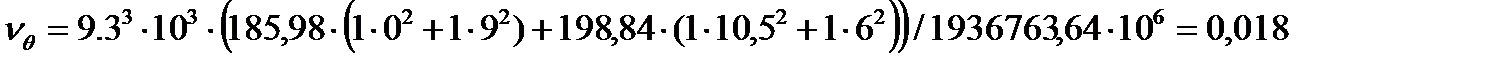
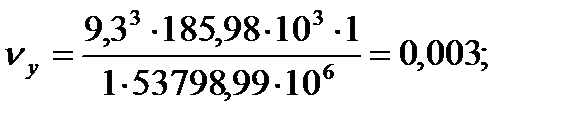
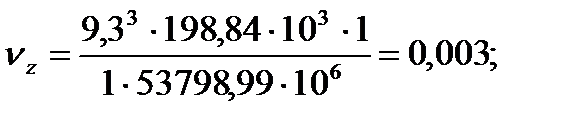


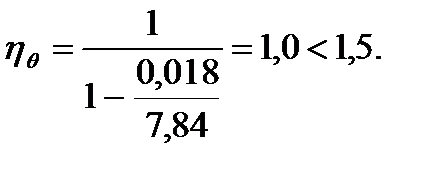
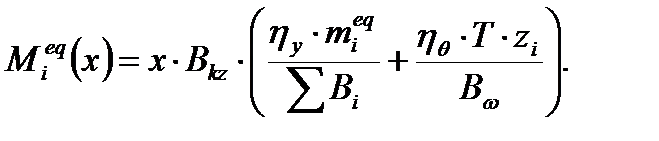
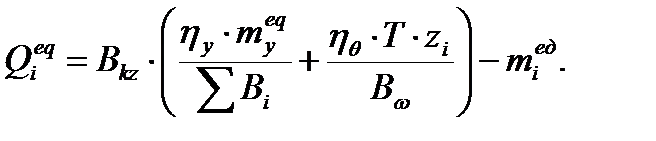
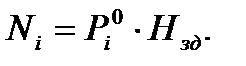
 где
где .
.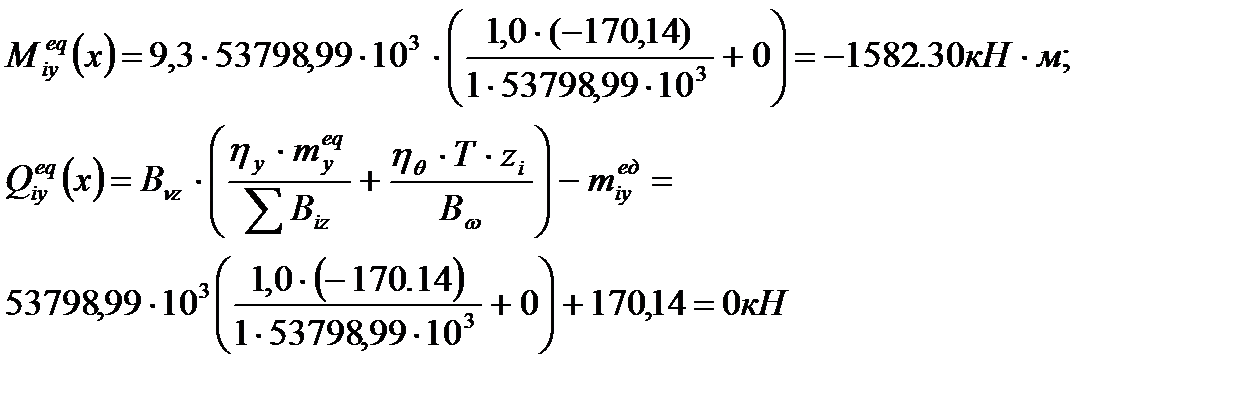
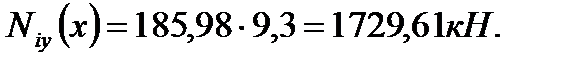
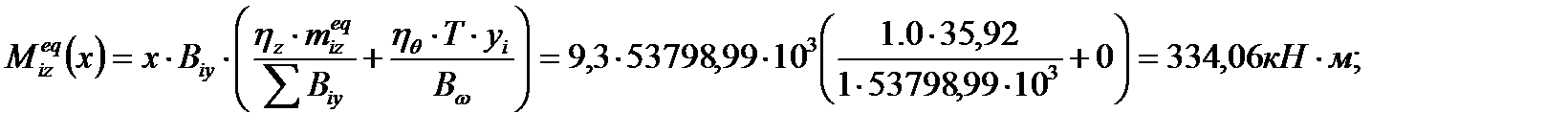


 где
где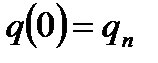 - ветровая нагрузка на здание в уровне верха здания;
- ветровая нагрузка на здание в уровне верха здания;
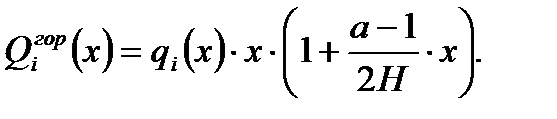 Х=Н.
Х=Н.
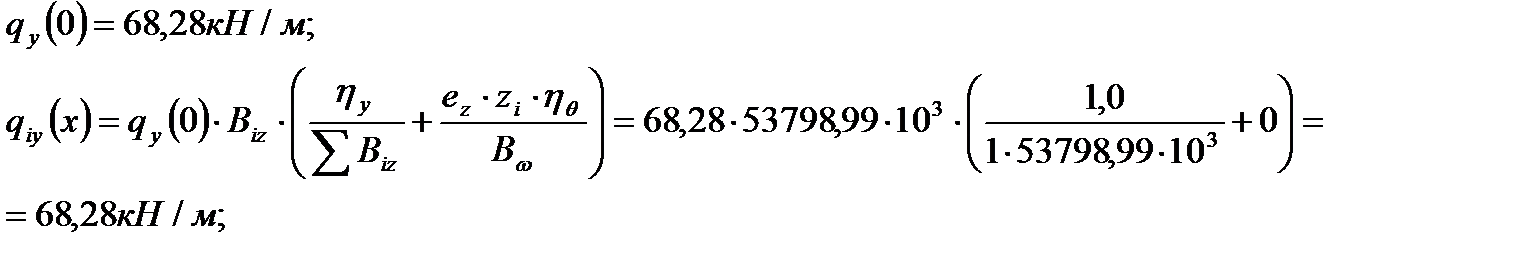
 ;
;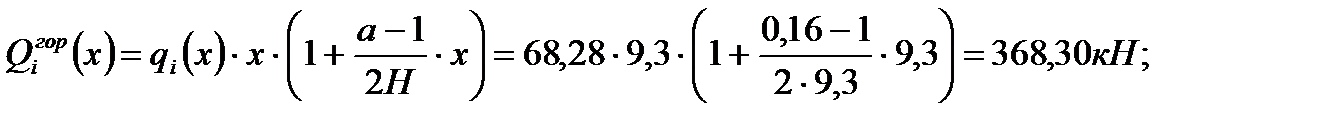
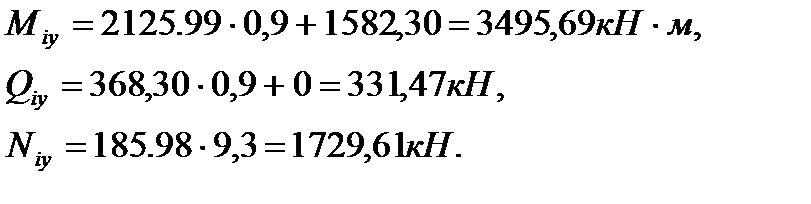
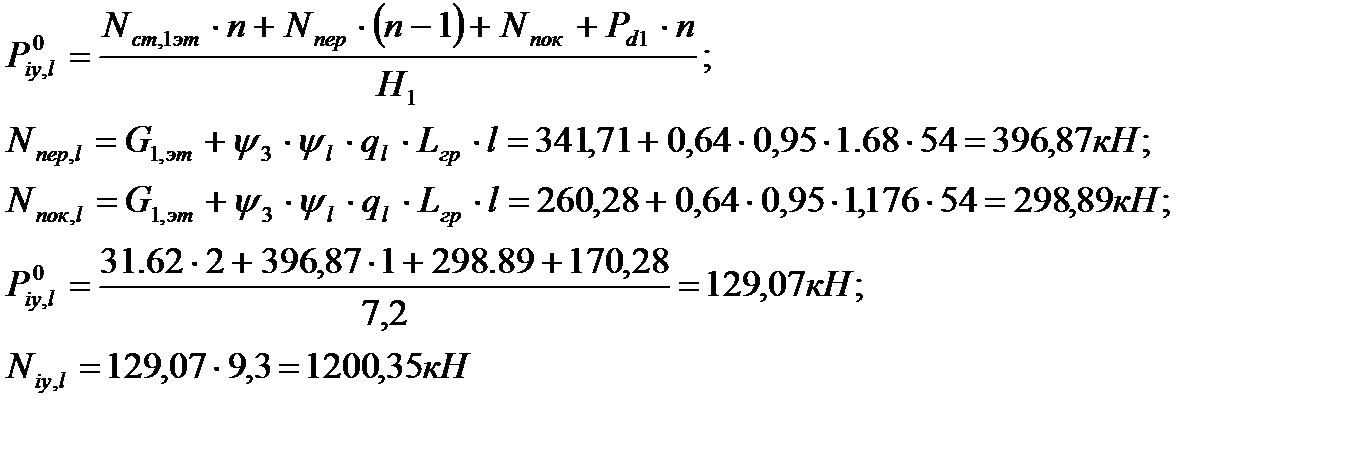
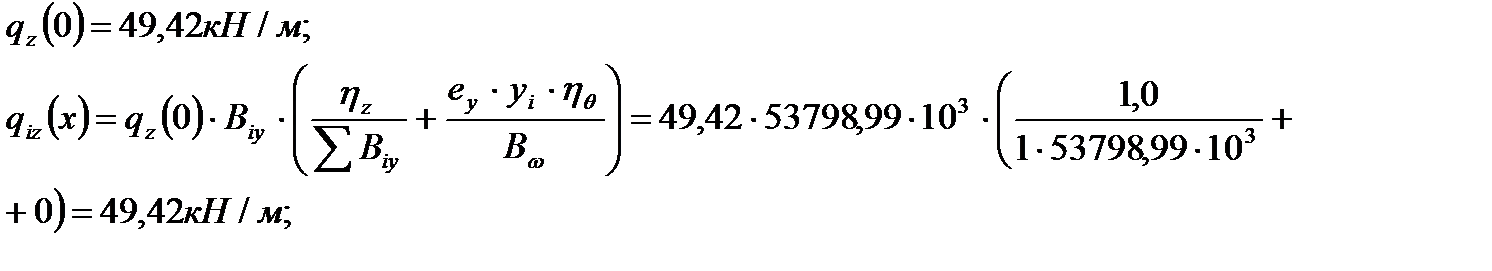
 ;
;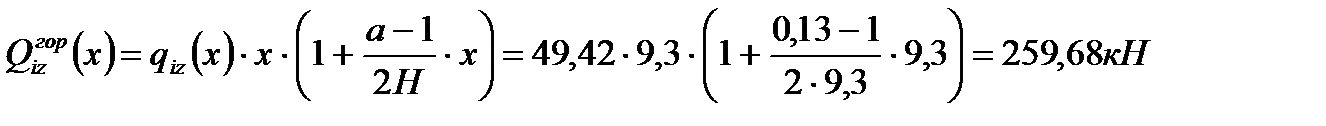 ;
;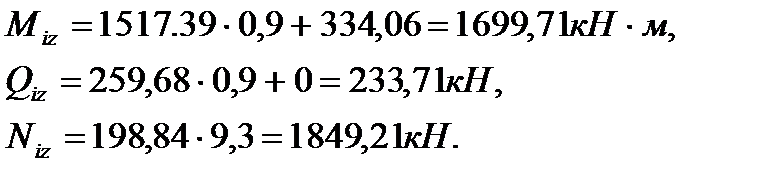

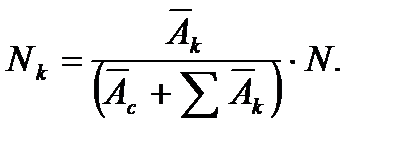
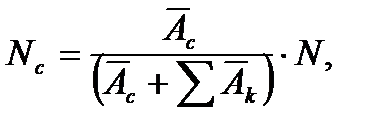 где
где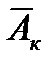 - осевая жесткость колонны;
- осевая жесткость колонны;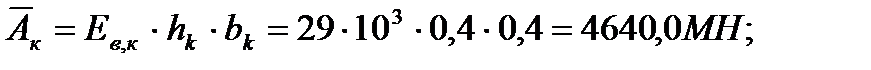 где
где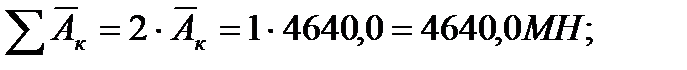
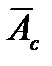 - осевая жесткость стенки диафрагмы;
- осевая жесткость стенки диафрагмы;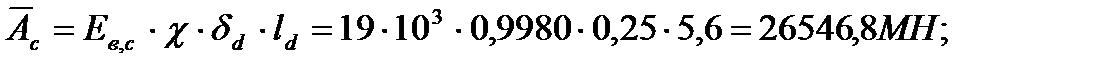
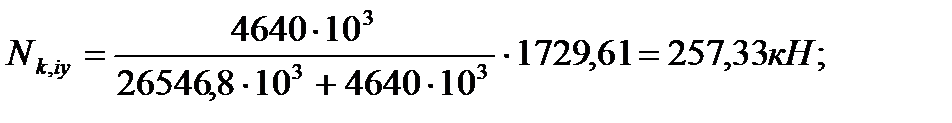
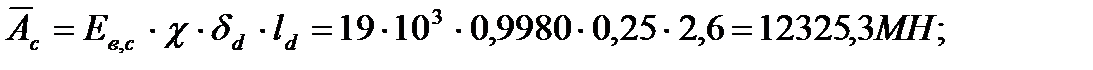
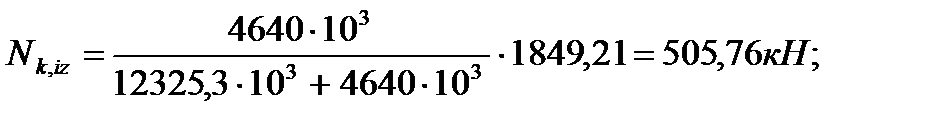
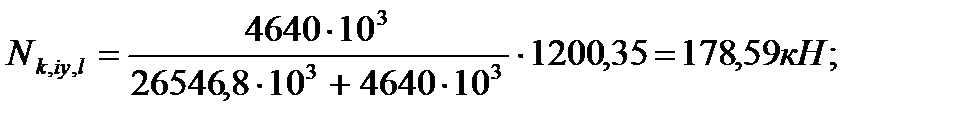
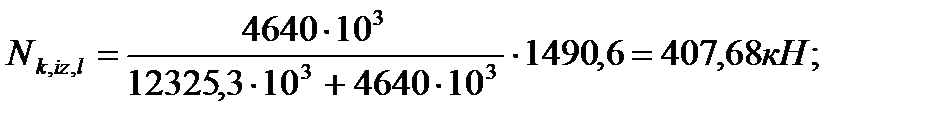
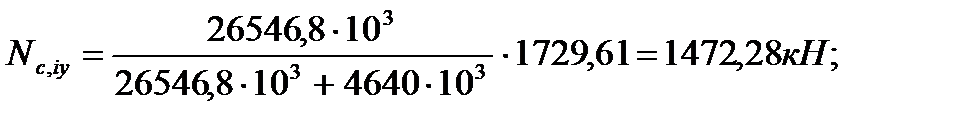


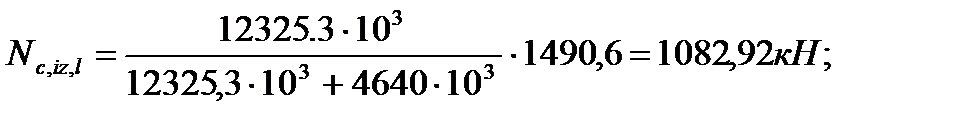
 ,
,  .
.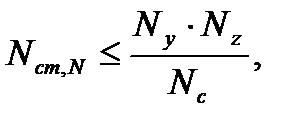 где
где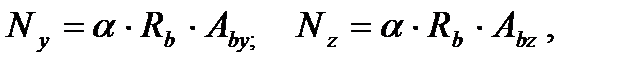 где
где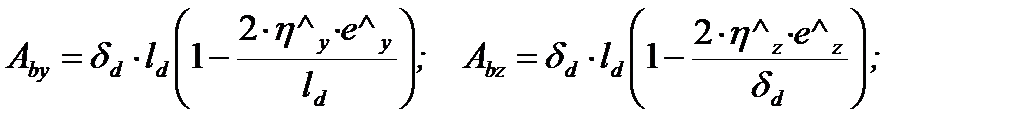
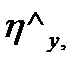
 - коэффициенты продольного изгиба;
- коэффициенты продольного изгиба;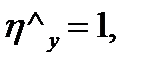
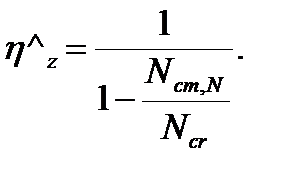
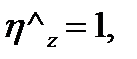
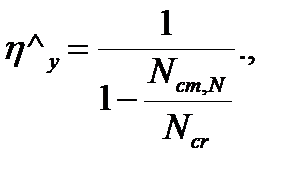
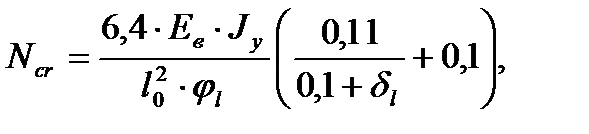 где
где
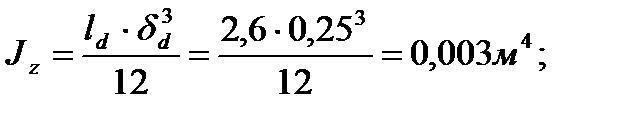
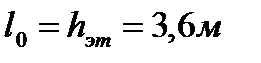 - расчетная длина диафрагмы жесткости в направлении большей гибкости;
- расчетная длина диафрагмы жесткости в направлении большей гибкости;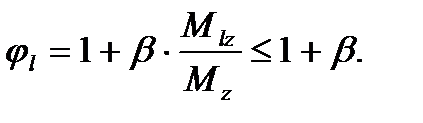
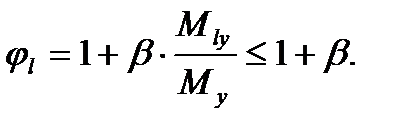

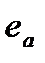 - случайный эксцентриситет
- случайный эксцентриситет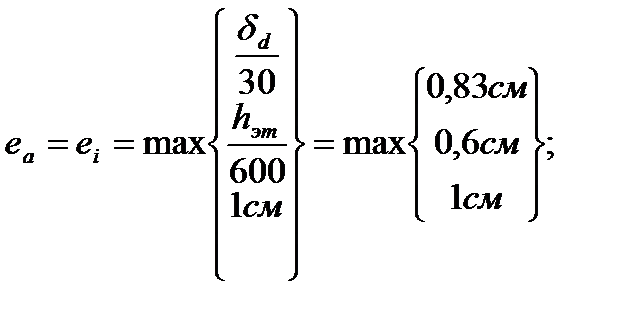

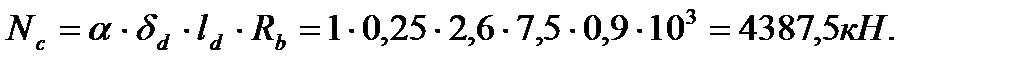
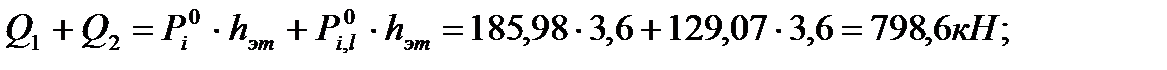
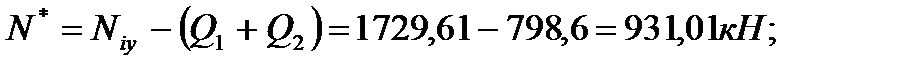
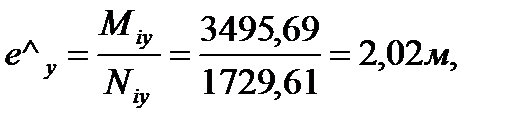
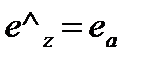
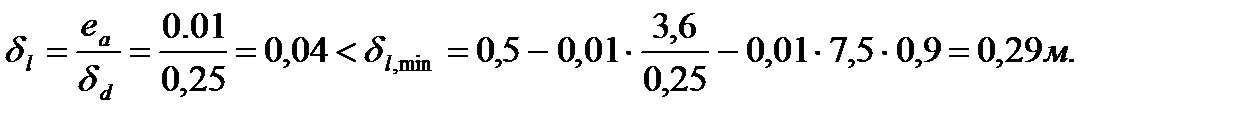
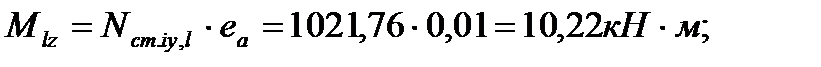
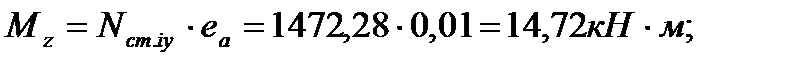

 где
где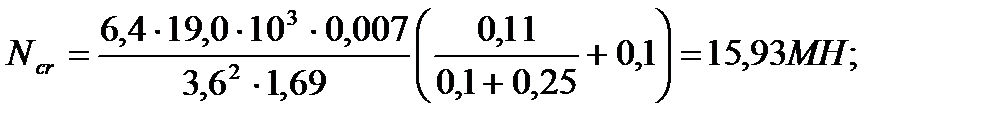
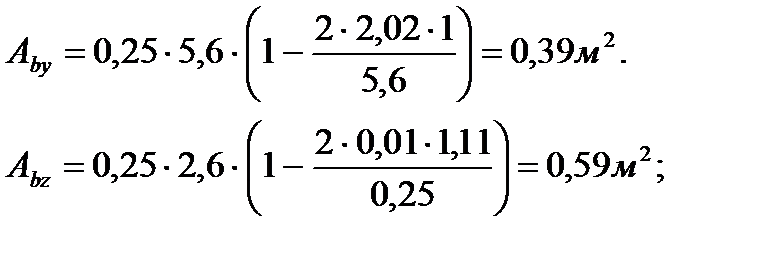
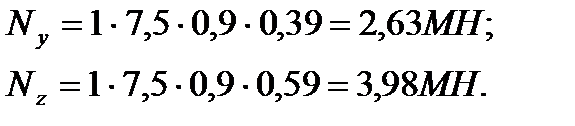
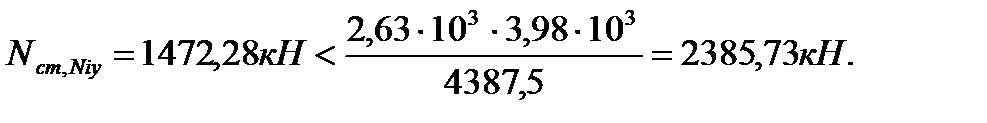
 где
где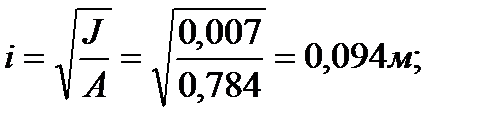
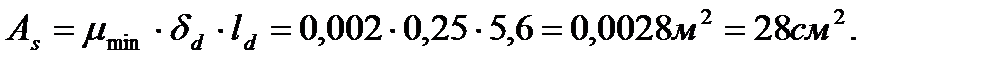
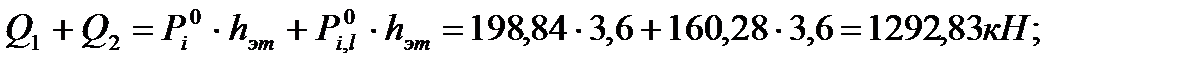



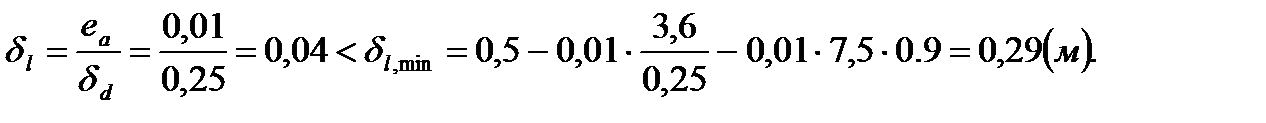
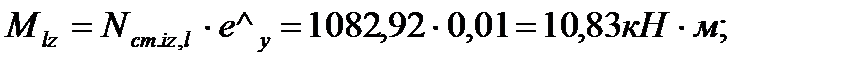


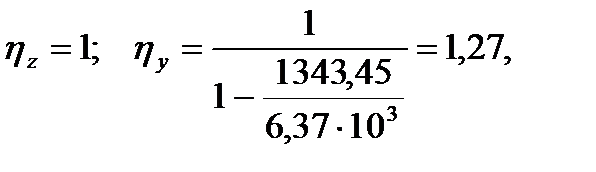 где
где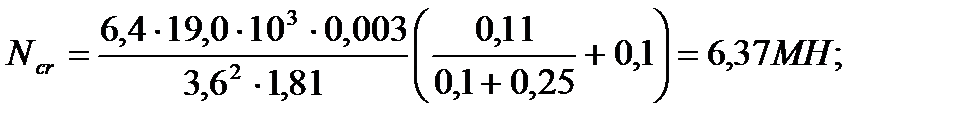
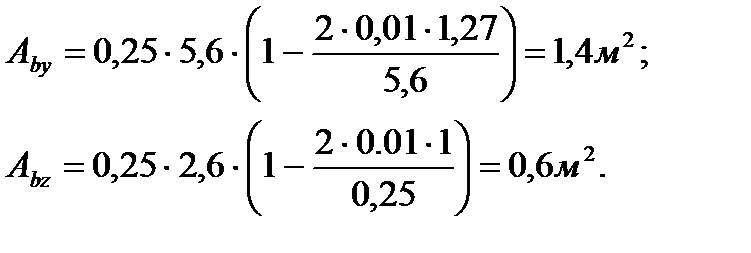
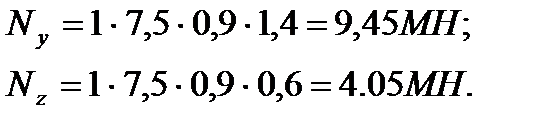
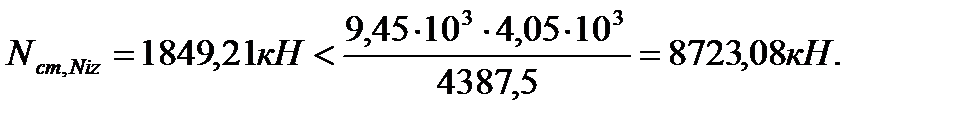
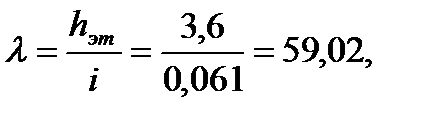 где
где
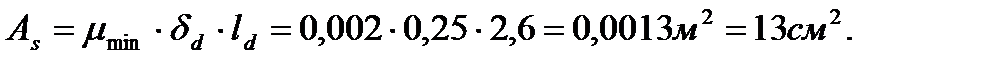
 где
где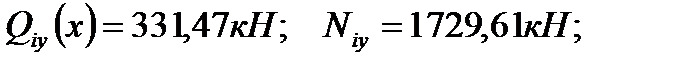
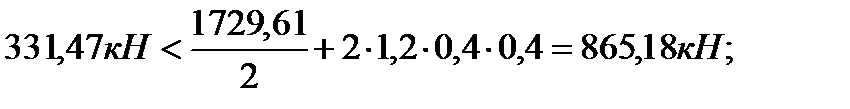
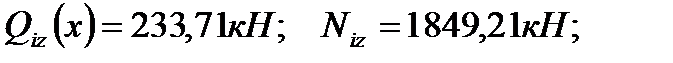



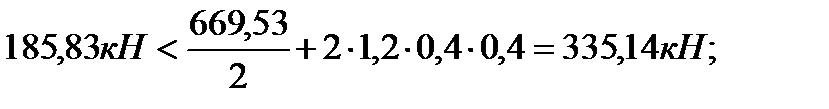

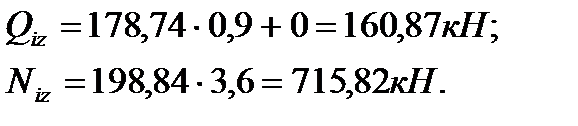
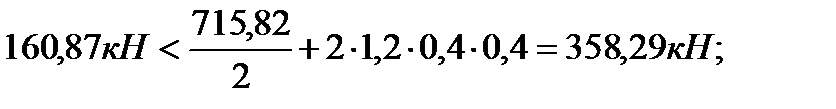
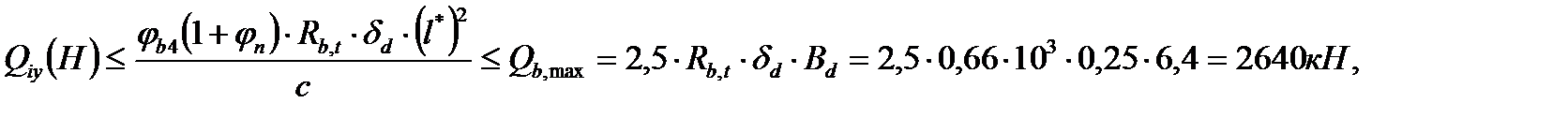 где jв4=1,5 – коэффициент для тяжелого бетона;
где jв4=1,5 – коэффициент для тяжелого бетона;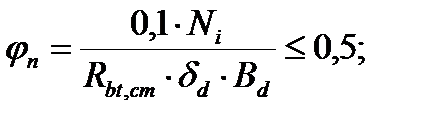
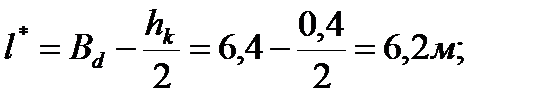
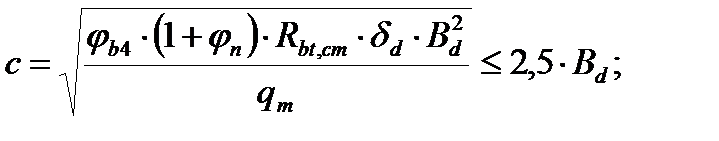

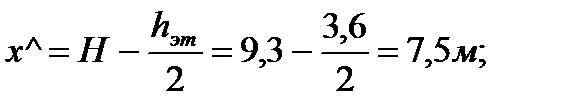
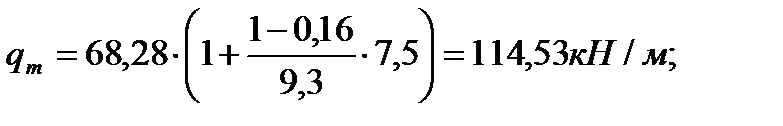
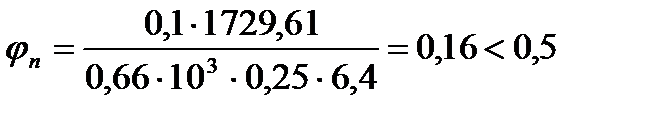 ;
; ;
;

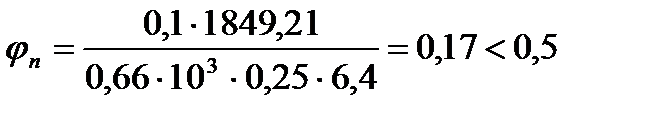 ,
,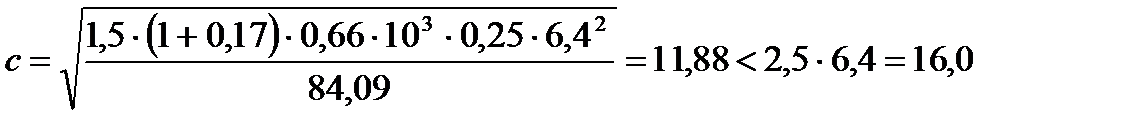 ;
;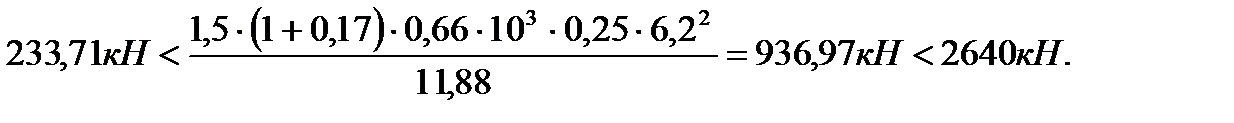
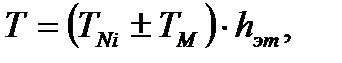 где
где - для диафрагм непосредственно воспринимающих нагрузку от перекрытия, параллельных оси Y;
- для диафрагм непосредственно воспринимающих нагрузку от перекрытия, параллельных оси Y;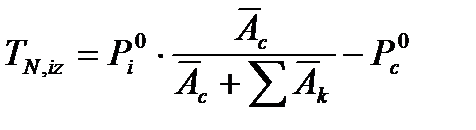 - для диафрагм непосредственно воспринимающих нагрузку от перекрытия, параллельных оси Z;
- для диафрагм непосредственно воспринимающих нагрузку от перекрытия, параллельных оси Z;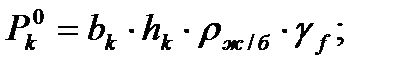

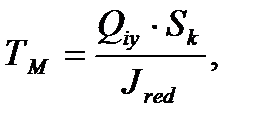 где
где ;
;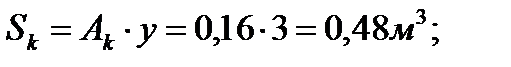
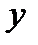 - половина расстояния между осями.
- половина расстояния между осями.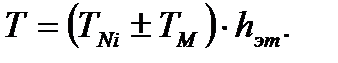
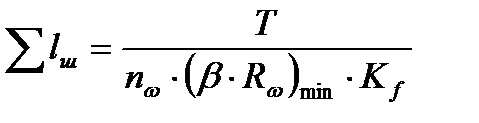 , где
, где , где
, где