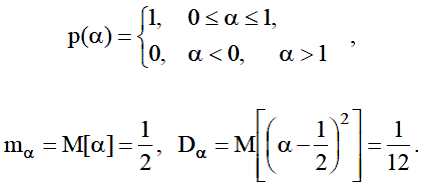Оценка дискретной случайной величины (вероятности события)
В ходе ИМ часто оценивают вероятности или процентные отношения для компонентов отклика, описывающих наступление того или иного события (исхода функционирования системы). Случайная величина В качестве оценки вероятности
где Требуется по методу доверительных интервалов найти число испытаний, при котором
где Можно переписать исходное неравенство
Величина
При
Итоговые уравнения, связывающие
Чтобы избавиться от неизвестного значения В результате получаем выражения для гарантированных значений
8. Датчики случайных чисел. Алгоритмы моделирования равновероятной и гауссовской случайных величин (1,2,3).
Датчик случайных чисел - алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению. Базовым алгоритмом является алгоритм датчика стандартной равномерно распределенной случайной величины:
|
в каждой реализации может принимать два значения: единица с вероятностью «хорошего» исхода 
и ноль с вероятностью «плохого» исхода 
.
,
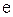– количество интересующих исходов в 
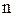реализациях.
,
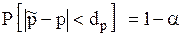– доверительный интервал.
в виде
.
, 
.
и 
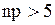или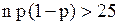 
можно пользоваться гауссовской аппроксимацией величины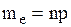 
. Отсюда получим:
, 
.
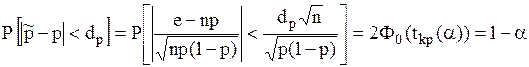
на величину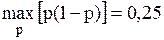 
.
, 
.
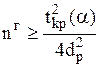