Соотношения для требуемого объема испытаний в модельном эксперименте при оценке среднего
Предположим, сначала, что ошибка оценки отклонения в каждой реализации распределена по гауссовскому или нормальному закону. Неравенство
Отсюда следует, что величину доверительного интервала можно определить, используя t-статистику или распределение Стьюдента с k-степенями свободы
Z – нормально распределенная величина с нулевым средним и единичной дисперсией;V – независимая от случайная величина, имеющая
подчиняется распределению Стьюдента с n-1 степенями свободы. Реальное использование полученных соотношений в ИМ осно-вано на проведении пробной оценки доверительного интервала или введении правила автоматического останова процесса имита-ции для получения интересующей точности. При n>30 t-распределение хорошо аппроксимируется гауссовским. При этом
Предположение о нормальности распределения ошибок оценки отклика в каждой реализации может быть неверным. Тогда используется неравенство Чебышева
6. Тактическое планирование. Соотношения для требуемого объема испытаний в модельном эксперименте при оценке дисперсии (1,2,3).
См. первую часть пятого вопроса + продолжение этого вопроса Исходное неравенство
Величина
где величина
Итоговые уравнения, связывающие
7. Тактическое планирование. Соотношения для требуемого объема испытаний в модельном эксперименте при оценке вероятности события (1,2,3).
См. первую часть пятого вопроса + продолжение этого вопроса
|

 эквивалентно следующему неравенству:
эквивалентно следующему неравенству:

 степенями свободы;
степенями свободы; независимые случайные величины, распределенные по нормальному закону
независимые случайные величины, распределенные по нормальному закону  Величина отношения в
Величина отношения в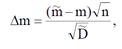
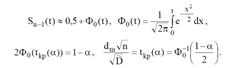


 можно переписать в виде
можно переписать в виде ,
,  .
. подчиняется
подчиняется  распределению с
распределению с  степенями свободы. Если
степенями свободы. Если 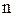 достаточно велико, то ее можно рассматривать как распределенную по нормальному закону с параметрами
достаточно велико, то ее можно рассматривать как распределенную по нормальному закону с параметрами  ,
, 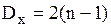 . Соответственно, можно переписать неравенство в виде
. Соответственно, можно переписать неравенство в виде ,
, распределена по стандартному гауссовскому закону. Отсюда
распределена по стандартному гауссовскому закону. Отсюда .
. и
и  ,
,  ,
,  .
.


