Соотношения для коэффициентов линейной регрессии
Требуется найти оценки коэффициентов b0,...,bk по результатам наблю- дения совокупности откликов системы y1,..., yN в ходе N экспериментов, считая, что полученные данные удовлетворяют линейной регрессии y1 = b0 x01+ b0 x01 +...+ b0 x01 + … y N = b0 x0N + b1 x1N +...+ bk xkN+ где xij, i = j = матическим ожиданием и дисперсию
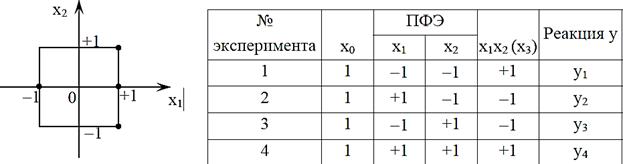
Столбцы матрицы X ортогональны, то есть Коэффициенты регрессии определяются в виде: Если теперь пронормировать факторы: Xi* = (xi – xi0) / Δxi, xi0 = ximin + Δxi; Δxi = (ximax − ximin) / 2, то условия ортогональности будут выполняться, если уровни факторов в ходе эксперимента будут взяты симметрично относительно начала координат и равны +1 и −1. Такой план эксперимента называется ортогональным N = Если осуществляют все возможные сочетания уровней факторов, то получают так называемый полный факторный эксперимент (ПФЭ). Полный факторный план при двух уровнях называют еще планом D или планом – 2k.
5. Тактическое планирование. Соотношения для требуемого объема испытаний в модельном эксперименте при оценке среднего
Тактическое планирование – планирование конкретного модельного эксперимента при фиксированных исходных данных. При фиксированных исходных данных модельный эксперимент состоит из серии повторяющихся имитаций процесса функционирования системы, что позволяет получить усредненную картину относительно ее эффективности с учетом случайного характера протекающих процессов и явлений. Тактическое планирование сводится к решению двух типов задач: 1. Определение начальных условий в той мере, в какой они влияют на установление стационарного режима работы модели; 2. Снижение погрешности (дисперсии) получаемых при моделировании оценок реакции системы при одновременном сокращении объема испытаний (числа прогнозов).
Первая задача тактического планирования в рамках рассмотренных подходов решается с использованием, в основном, эвристических приемов, опирающихся на знание физики разыгрываемых в ИМ процессов.
Вторая задача тактического планирования может быть решена строго математически. Это решение сводится к определению гарантированного объема испытаний (размера выборки, числа прогонов) для получения требуемой точности оценивания компонентов отклика системы, описывающих ее эффективность.
Снижение или исключение влияния начального периода времени при переходе в установившийся режим должно осуществляться при проведении каждого прогона модели. При этом используют три основных способа: 1. увеличение длительности каждого прогона так, чтобы влияние переходного периода было бы заведомо незначительным; 2. исключение из рассмотрения начального периода (введение этапа предварительной «раскрутки» процесса имитации); 3. искусственный подбор близких к режимным начальных условий для каждой реализации.
|

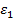 ,
,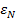 ,
,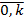 ; j =
; j = 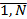 − значения факторов в ходе экспериментов;
− значения факторов в ходе экспериментов; 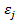 ,
,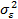 .
.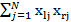 =0,l ≠ r, 0 ≤ r,l ≤ k.
=0,l ≠ r, 0 ≤ r,l ≤ k. =
=  ,i=
,i= 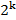 .
.