Оценка качества и существенности уравнения связи признаков.Качество построенного уравнения регрессии оценивается с помощью средней ошибки аппроксимации. Такая оценка отвечает на вопрос о возможности использования полученного уравнения для дальнейшего анализа и прогнозирования. Средняя ошибка аппроксимации строится исходя из разности фактических значений результата и его теоретических значений, полученных по уравнению регрессии. Если фактические значения (у) и теоретические значения ( Считается, что качество уравнения удовлетворительное и его можно использовать для анализа и прогнозирования, если Оценка существенности уравнения связи проводится с использованием F-критерия Фишера. Выдвигается гипотеза о несущественности изучаемой связи признаков, т.е. о её случайном характере. Такая гипотеза называется нулевой и обозначается Н0. Нулевую гипотезу необходимо проверить. Для этого рассчитывают фактическое значение критерия Фишера по формуле:
Fфакт сравнивается с критическим значением Fкрит (табл f-критерия Фишера).Критическое значение – это максимальное значение f-критерия при котором принимается нулевая гипотеза, т.е.если Fфакт≤Fкрит – мы принимаем нулевую гипотезу(связь признаков случайна и не существенна), если Fфакт≥Fкрит – отвергаем нулевую гипотезу, связь признаков существенна, носит закономерный характер.
|
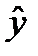)близки по величине, ошибка будет маленькой, если различия 
и 
большие, ошибка будет большой. Средняя ошибка аппроксимации рассчитывается по формуле: 
. Если средняя ошибка аппроксимации еще меньше и не превышает 5%, то качество построенного уравнения считается очень хорошим.
, где n- число единиц совокупности, m – число параметров уравнения регрессии.
